截段八面体堆积 matlab,截角八面体可以充满空间

原标题：截角八面体可以充满空间

触碰标题下面一行的“邵勇老师”查看所有文章；触碰“数学教学研究”, 关注本微信公众号(sx100sy)。本公众号内容均由邵勇(北京)本人独创，欢迎转发，但未经许可不能转载。每周推送两到三篇内容上有份量的数学文章，但在行文上力争做到深入浅出。几分钟便可读完，轻松学数学。

特别声明，本人未曾授权任何网站(包括微博)、公众号或其他什么号转载北京邵勇原创的“数学教学研究”公众号的内容。建议您一定直接关注本公众号(sx100sy)，这样有什么问题可以留言交流和发消息，我会诚恳回复。未经授权而转载我文章的地方丢失了很多功能，比如留言，比如发消息到我后台。未经授权而转载我文章的地方，毕竟还存留着贯穿于我文章中的图片(比如公式)，图片的右下角都有原公众号的水印“微信号:sx100sy”，通过在微信中搜索“sx100sy”，一定可以找到原始的公众号，也就是本公众号《数学教学研究》(sx100sy)并加以关注。本公众号才是良好的交流平台和文明的生态环境。

在2021年春节这个欢天喜地的日子里，给关注我的文章的朋友们送去最真挚的祝福，祝您新春快乐，牛年大吉！

今天介绍由柏拉图体和(或)阿基米德体的组合可以铺满整个空间的第五种情况(也是最后一种情况)——只用一种阿基米德体而不用柏拉图体就可以办到，这也是唯一一种只用一种阿基米德体就可以做到的情况。只用一种柏拉图体实现空间满铺也是一种情况，那就是使用正方体(其他四种柏拉图体单独都做不到)。正方体情况若算作第一种，本篇所讲算作第五种，那么，中间的第二、三、四种就都是由两种立体(或两种柏拉图体，或一种柏拉图体和一种阿基米德体)的组合铺满空间。这三种我之前分三期有过详细讲解，它们的链接在文后。

我们知道阿基米德体中的截角多面体包括截角四面体、截角正方体、截角八面体、截角十二面体和截角二十面体(足球，足球烯的结构)。本篇先简单回顾一下截角八面体。然后讲解 无数多个相同的截角八面体如何能够填满整个空间。下图为截角八面体。

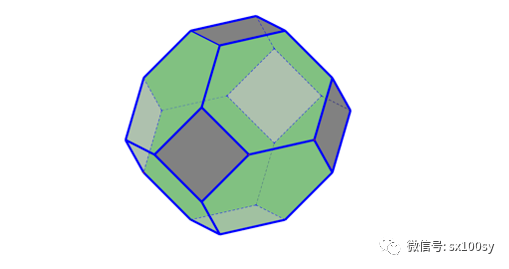
你能想像出如何把无数多个相同大小的截角八面体拼成之间没有缝隙的整体吗？首先要仔细研究一下它的特点。它有六个正方形面，还有八个正六边形面。若把两个截角八面体拼在一起，肯定是正方形面对接正方形面，正六边形面接对正六边形面。我们还注意到，靠一条棱相连接的两个正方形面都是互相垂直的关系。所以，我们可以试着把四个 截角八面体互相紧挨着拼到一起，就象“四喜丸子”。为了看得更清楚，我画了两组“四喜丸子”，并且并排放在一下。如下图所示。

观察上图中黄色圆圈圈起来的部分。其中有四个正六边形，它们分别来自四个截角八面体。这四个六边形中间是一个正方形空框，它的大小与截角八面体的正方形面的大小一样。这四个六边形与这个空正方形一起，构成了一个“无底的碗”，碗口朝向我们。再观察一下截角八面体，一个正方形面的四边分别连接着一个正六边形。通过计算可以得知，黄色圆圈圈起来的这个碗状“凹穴”，正好可以把截角八面体的五个面对插进去，并且严丝合缝。上图中还有另外两个同样的凹穴，每个凹穴都可以填入一个截角八面体的五个面，三个被插进去的截角八面体之间正好是通过正方形面紧贴在一起一字排开。于是，我们找到了拼接无数同样大小截角八面体的方法：像上图那样竖起一面有无数正方形空框的墙，并且让它无限大。同样的再竖起另一面完全一样的墙。把这一面墙的凸穴与另一面墙的凹穴对插在一起。无数多这样的墙就可以拼接出整个空间。

看一下铺满整个空间后，一个这样的截角八面体的一条棱都连接着哪些“体”，又连接着哪些“面”。不难看出，每条棱都连接着三个截角八面体；每条棱也都连接着一个正方形面和两个正六边形面。也就是说，我们只用了一种阿基米德体就拼出了整个空间，并且在这个拼接中，所有的棱的地位都是相同的。

(注意，柏拉图体和阿基米德体都是由正多边形表面围成的立体。以前也讲过菱形十二面体可以填满空间，但它的面不是正多边形。下面的五种情况要求所使用的立体都是柏拉图体和(或)阿基米德体。)

第一种：最简单的由完全一样的柏拉图体之一的正方体拼接而成(因为太过简单，图和讲解就省略不讲了)

第二种：由正八面体和正四面体组合拼接而成。

《 有关正八面体、正四面体的有趣问题 》

(2021年1月3日)

第三种：由正四面体和截角四面体组合拼接而成。

《 正四面体与截角四面体可以铺满空间 》

(2021年1月6日)

第四种：由正八面体和截半八面体组合拼接而成。

《 正八面体与截半八面体的组合可铺满空间 》

(2021年2月11日)

第五种：由一种阿基米德体—— 截角八面体独自拼接而成(本期)。返回搜狐，查看更多

责任编辑：