笛卡尔心形函数表达式_一个心形线引发的故事

最新推荐文章于 2025-02-14 09:59:20 发布

蔡佳人

最新推荐文章于 2025-02-14 09:59:20 发布

阅读量2.7w

点赞数 3

文章标签：笛卡尔心形函数表达式

本文链接：https://blog.csdn.net/weixin_29710393/article/details/112368376

版权

本文深入探讨了笛卡尔心形线的定义、方程推导、性质及在考试中的应用。通过极坐标和HTML画图，展示了如何绘制心形线，并提供了动态效果的实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

心形线除了在考试中会遇到，它还是表白时常用来装逼的曲线之一。为了更好地表(zhuang)白(bi),我们一起深入的了解一下这个曲线。

【关于定义】

心形线，是一个圆上的固定一点在它绕着与其相切且半径相同的另外一个圆周滚动时所形成的轨迹，因其形状像心形而得名。来个动图更直接

这里的C代表我，M当然是代表了高冷的mathematics

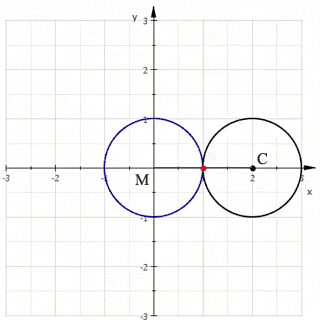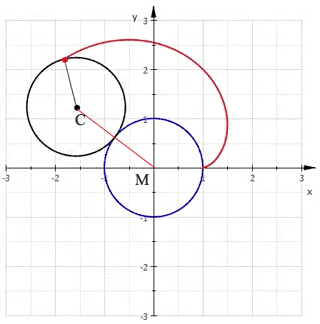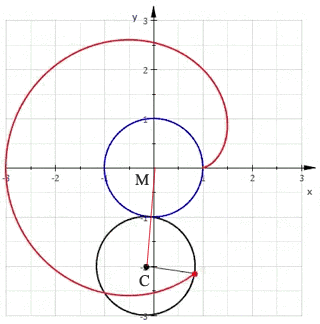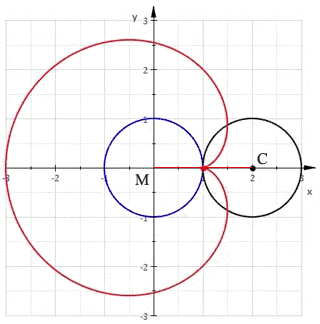
看这个曲线是不是像极了爱(Pi)情(gu)，在我看来这分明是一个舔狗的运动轨迹，不管你

如何运动，我

不为之所动，哈哈哈，扯远了。

上图的曲线方程写出来是这样的

看到这个方程有木有似曾相识的赶脚，这里的

是指圆的直径，也可以理解为两个圆心的距离，

是动圆定点转过的角度。其实心形方程有四个，分别从不同的方向。

那么这些方程怎么来的呢？我们找其中一个来推导一下。

【心形线方程的推导】

如上图，设圆的直径为

，心形上的点

的极坐标为

,由对称性可知，四边形

是等腰梯形。那么我们可以推出

所以

【心形线的性质】

既然这个曲线是由两个圆而来，那么必然跟圆有着密不可分的关系。

弧长：是圆直径的

倍，也就是

这个数字是不是很熟悉，在摆线里也看到过，摆线的弧长也是8a,不过一个是半径一个是直径，不要搞错噢。

面积：是圆面积的

倍。

这两个值我们可以计算出来，过程如下：

弧长可以直接套公式

极坐标下的弧长公式为：

【举栗】求心形线

的长度。

由

所以

极坐标下的曲边扇形面积公式为：

【举栗】求心形线

围成的平面区域面积

套公式：

【心形线在考试中的应用】

直接上题目：

这是2012年考研数二的真题。

我们来分析一下这道二重积分的题目，一般来说二重积分要么考察被积函数，要么从积分区域为难你，或者考察对称性奇偶性。这题的被积函数没什么文章，看到这个积分区域很开心的有木有，积分区域是一个直径为1的圆绕另一个直径为1的圆运动形成的轨迹，角度的取值决定了这是半个心（pi）形（gu）。

详细计算过程可以参考各大真题解析

【由极坐标方程画图】

如果给出极坐标方程，在我不认识这是心形的情况下怎么来画出这个图形呢？

举个栗子

画

的曲线

分析：首先这个曲线是关于

轴对称的图形，因为

，所以

在图形上。

当

从

增加至

时,

从

减至

,而

从最小值0增加至最大值

,当

继续从

到

时,

从

回到

,而

从

减少回到

当

时曲线开始重复.

曲线以斜率

离开原点,又以斜率

回到原点

我们可以列一个

从

到

的表,画出各个点,通过每个点描出曲线,再对X轴反射曲线以完成曲线.

根据这个表描出各个点:

【用html画心形线】

用html的画布功能

标签画心形线,<canvas>标签本身没有绘图能力,它只是一个图形的容器,可以结合JavaScript来实现。

画图的思路就是根据方程表达式得到所有点的坐标，把每个点连接起来，填充就行成了一个心形。

在html中可以用直角坐标和极坐标两种画法。

我们用直角坐标来画。

在直角坐标系下心形线对应的参数方程为：

实现代码为：

<!DOCTYPE html>
<html lang="en">
    <head>
        <meta charset="UTF-8">
    </head>
    <body>
        <canvas width="400" height="400"></canvas>
        <script>
            var canvas = document.querySelector('canvas');
            var context =  canvas.getContext('2d');
            context.lineWidth = 3;
            context.translate(200,200);
            var t=0;
            var maxt = 2*Math.PI;
            var vt = 0.01;
            var maxi = Math.ceil(maxt/vt);
            var pointArr=[];
            var x=0;
            var y=0;
            for(var i=0;i<=maxi;i++){
                x=30*(2*Math.sin(t)+Math.sin(2*t));
                y=30*(2*Math.cos(t)+Math.cos(2*t));
                t+=vt;
                pointArr.push([x,y]);
            }
            context.moveTo(pointArr[0][0],pointArr[0][1]);
            draw();
            function draw(){
                context.fillStyle='#c00';
                for(var i=1;i<pointArr.length;i++){
                    x= pointArr[i][0];
                    y= pointArr[i][1];
                    context.lineTo(x,y);

                }
                context.fill();
            }


        </script>
    </body>
</html>

效果图是这样的：

换成空心的，把fill()方法换成sroke().

function draw(){
                context.strokeStyle='#c00';
                for(var i=1;i<pointArr.length;i++){
                    x= pointArr[i][0];
                    y= pointArr[i][1];
                    context.lineTo(x,y);

                }
                context.stroke();

效果如下：

话说这个心形实在不好看。我们可以做一个形状好看一点的并让它动起来。

最终效果是这样的：

跟上面的画法一样，需要找到这个图形的参数方程：

实现代码：

<!doctype html>
<html lang="en">
 <head>
  <meta charset="UTF-8">
 </head>
 <body>
    <canvas width="400" height="400"></canvas>
	<script>
		var canvas = document.querySelector('canvas');
		var context = canvas.getContext('2d');  
		context.lineWidth = 3;
		context.translate(200,200); 
		var t=0;
		var vt = 0.01;
		var maxt = 2*Math.PI;
		var maxi = Math.ceil(maxt/vt);
		var pointArr=[];
		var size = 10;
		var x=0;
		var y=0;
		for(var i=0;i<=maxi;i++){
			// x=16 * (sin(t)) ^ 3;
			var x = 16 * Math.pow(Math.sin(t),3);
			// y=13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t)
			var y = 13 * Math.cos(t) - 5 * Math.cos(2 * t) -2 * Math.cos(3 * t)- Math.cos(4 * t);
			t+=vt;
			pointArr.push([x*size,-y*size]); 
		}
		context.moveTo(pointArr[0][0],pointArr[0][1]);
		function draw(){
			context.fillStyle='#c00';
			for(var i=1;i<pointArr.length;i++){
				x = pointArr[i][0];
				y = pointArr[i][1];
				context.lineTo(x,y);
			}
			context.fill();
		}
        		var idx = 1;
        		context.fillStyle='#c00';
        		context.strokeStyle='#c00';
        		var tt = '';
        		slowly();
        		function slowly() {
        			x = pointArr[idx][0];
        			y = pointArr[idx][1];
        			context.lineTo(x,y);
        			if(idx+1 >= pointArr.length){
        				context.fill();
        				clearTimeout(tt);
        			} else {
        				idx++;
        				clearTimeout(tt);
        				tt = setTimeout("slowly()",20);
        				context.stroke();
        			}
        		}
	</script>
 </body>
</html>

最后来一张动图效果图：