重叠面积_初中数学动点难题：数轴上两长方形面积重叠问题（变型题）

数轴上的动点问题难不难？难！！“书上有路勤为径，学海无涯苦作舟”，再难的题目都有解题方法。笔者继续就浙教版七年级数学---数轴上的动点问题变型题进行探究，同样分别用几何图形和代数方法解数轴上的动点问题。

如图，长方形OABC的边OA在数轴上，O为原点，长方形OABC面积为12. OC边长为3

⑴数轴上点A表示的数是----------------------。

⑵将长方形OABC沿OA所在直线水平移动，移动后的长方形记为O'A'B'C'.若移动后的长方形O'A'B'C'与原长方形OABC重叠部分的面积恰好等于原长方形OABC的面积的一半时，则数轴上点A'表示的数是多少？

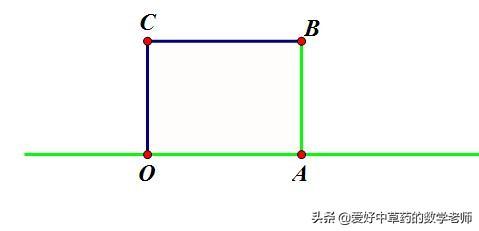
解：⑴.由题意得：

A表示的数为：4

⑵问移动到A'在数轴上是什么位置的时候，长方形O'A'B'C'与原长方形OABC重叠部分的面积恰好等于原长方形OABC的面积的一半

一、利用几何画板来演示，长方形的移动变化(如图重合时的情形)：

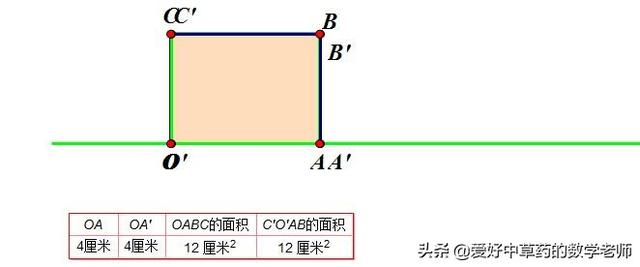
下面我们来移动长方形，使得重叠部分C'O'AB的面积恰好等于原长方形OABC的面积的一半(如图3)：

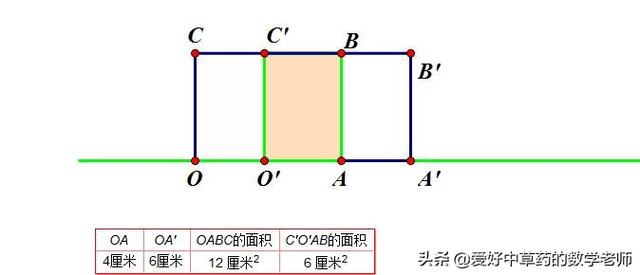
对比移动前后图，我们发现面积：C'O'AB=1/2OABC 时，OA'由4移动到6的位置，这样我们利用图形就解得A'表示的数为6.

二、下面笔者用代数的方法解题：

解：设A'表示的数为x,由题意得：

∵0A=4，OC=3

∴[4-(x-4)]*OC=6

解之得：

x=6

答：略

此题用方程代数解题，主要考察学生空间想象能力，

第一步：OA'-OA，

第二步：OA-(OA'-OA)

第三步：【OA-(OA'-OA)】*OC

最后：解方程。

探究变型题二(供读者自行解答)：

长方形OABC的边OA在数轴上，O为原点，长方形OABC面积为12. OC边长为3。若D为线段AA' 的中点，点E在线段OO'上，且OE=1/3OO',求当长方形OABC移动的距离为多少时，D、E两点到原点O的距离相等？

PS:

码字不易，欢迎读者在评论区进行评论，您的建议和评论对我创作大于裨益，欢迎转发与关注，谢谢！----爱好中草药的数学老师。