From Wikipedia, the free encyclopedia
In optics, a Gaussian beam is a beam of electromagnetic radiation whose transverse electric field and intensity (irradiance) distributions are well approximated by Gaussian functions. Many lasers emit beams that approximate a Gaussian profile, in which case the laser is said to be operating on the fundamental transverse mode, or "TEM00 mode" of the laser's optical resonator. When refracted by a diffraction-limited lens, a Gaussian beam is transformed into another Gaussian beam (characterized by a different set of parameters), which explains why it is a convenient, widespread model in laser optics.
Instantaneous intensity of a Gaussian beam.
The top portion of the diagram shows the two-dimensional intensity profile of a Gaussian beam that is propagating out of the page. The blue curve, below, is a plot of the electric field amplitude as a function of distance from the center of the beam. The black curve is the corresponding intensity function.
A 5 mW green laser pointer beam profile, showing the TEM00 profile
The mathematical function that describes the Gaussian beam is a solution to the paraxial form of the Helmholtz equation. The solution, in the form of a Gaussian function, represents the complex amplitude of the beam's electric field. The electric field and magnetic field together propagate as an electromagnetic wave. A description of just one of the two fields is sufficient to describe the properties of the beam.
The behavior of the field of a Gaussian beam as it propagates is described by a few parameters such as the spot size, the radius of curvature, and the Gouy phase.[1]
Other solutions to the paraxial form of the Helmholtz equation exist. Solving the equation in Cartesian coordinates leads to a family of solutions known as the Hermite–Gaussian modes, while solving the equation in cylindrical coordinates leads to the Laguerre–Gaussian modes.[2] For both families, the lowest-order solution describes a Gaussian beam, while higher-order solutions describe higher-order transverse modes in an optical resonator.Contents [hide]
1 Mathematical form
2 Beam parameters
2.1 Beam width or spot size
2.2 Rayleigh range and confocal parameter
2.3 Radius of curvature
2.4 Beam divergence
2.5 Gouy phase
2.6 Complex beam parameter
3 Power and intensity
3.1 Power through an aperture
3.2 Peak and average intensity
4 Derivation
5 Higher-order modes
5.1 Hermite-Gaussian modes
5.2 Laguerre-Gaussian modes
5.3 Ince-Gaussian modes
5.4 Hypergeometric-Gaussian modes
6 See also
7 Notes
8 References[edit]Mathematical form
The Gaussian beam is a transverse electromagnetic (TEM) mode.[3] A mathematical expression for its complex electric field amplitude can be found by solving the paraxial Helmholtz equation, yielding[1]
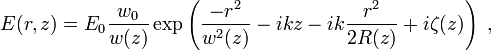
where[1]
is the radial distance from the center axis of the beam,
is the axial distance from the beam's narrowest point (the "waist"),
is the imaginary unit (for which
),
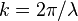is the wave number (in radians per meter),
,
is the radius at which the field amplitude and intensity drop to 1/e and 1/e2 of their axial values, respectively,
is the waist size,
is the radius of curvature of the beam's wavefronts, and
is the Gouy phase shift, an extra contribution to the phase that is seen in Gaussian beams.
Additionally, the field has a time dependence factor
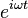that has been suppressed in the above expression.
The corresponding time-averaged intensity (or irradiance) distribution is
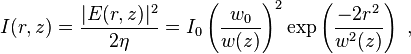
where
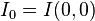is the intensity at the center of the beam at its waist. The constant
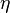is the characteristic impedance of the medium in which the beam is propagating. For free space,
.[edit]Beam parameters
The geometry and behavior of a Gaussian beam are governed by a set of beam parameters, which are defined in the following sections.[edit]Beam width or spot sizeSee also: Beam diameter
Gaussian beam width w(z) as a function of the axial distance z. w0: beam waist; b: depth of focus; zR: Rayleigh range;
: total angular spread
For a Gaussian beam propagating in free space, the spot size (radius) w(z) will be at a minimum value w0 at one place along the beam axis, known as thebeam waist. For a beam of wavelength λ at a distance z along the beam from the beam waist, the variation of the spot size is given by[1]
where the origin of the z-axis is defined, without loss of generality, to coincide with the beam waist, and where[1]
is called the Rayleigh range.[edit]Rayleigh range and confocal parameter
At a distance from the waist equal to the Rayleigh range zR, the width w of the beam is[1]
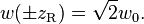
The distance between these two points is called the confocal parameter or depth of focus of the beam:
[edit]Radius of curvature
R(z) is the radius of curvature of the wavefronts comprising the beam. Its value as a function of position is[1]
[edit]Beam divergence
The parameter
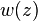increases linearly with
for
. This means that far from the waist, the beam is cone-shaped. The angle between the straight line
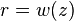and the central axis of the beam (
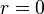) is called the divergence of the beam. It is given by[1]
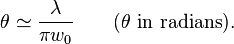
The total angular spread of the beam far from the waist is then given by
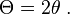
Because the divergence is inversely proportional to the spot size, a Gaussian beam that is focused to a small spot spreads out rapidly as it propagates away from that spot. To keep a laser beam very well collimated, it must have a large diameter. This relationship between beam width and divergence is due to diffraction. Non-Gaussian beams also exhibit this effect, but a Gaussian beam is a special case where the product of width and divergence is the smallest possible.
Since the gaussian beam model uses the paraxial approximation, it fails when wavefronts are tilted by more than about 30° from the direction of propagation.[4] From the above expression for divergence, this means the Gaussian beam model is valid only for beams with waists larger than about
.
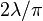Laser beam quality is quantified by the beam parameter product (BPP). For a Gaussian beam, the BPP is the product of the beam's divergence and waist size
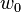. The BPP of a real beam is obtained by measuring the beam's minimum diameter and far-field divergence, and taking their product. The ratio of the BPP of the real beam to that of an ideal Gaussian beam at the same wavelength is known as M2 ("M squared"). The M2 for a Gaussian beam is one. All real laser beams have M2 values greater than one, although very high quality beams can have values very close to one.[edit]Gouy phase
The longitudinal phase delay or Gouy phase of the beam is[1]
The Gouy phase indicates that as a Gaussian beam passes through a focus, it acquires an additional phase shift of π, in addition to the usual
phase shift that would be expected from a plane wave.[1][edit]Complex beam parameterMain article: Complex beam parameter
Information about the spot size and radius of curvature of a Gaussian beam can be encoded in the complex beam parameter,
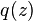:[5]
The reciprocal
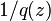shows the relationship between
,
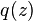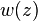, and
explicitly:[5]
The complex beam parameter plays a key role in the analysis of gaussian beam propagation, and especially in the analysis of optical resonator cavities using ray transfer matrices.
In terms of the complex beam parameter
, a Gaussian field with one transverse dimension is proportional to
In two dimensions one can write the potentially elliptical or astigmatic beam as the product
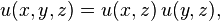
which for the common case of circular symmetry where
and
yields[6]
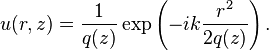[edit]Power and intensity[edit]Power through an aperture
The power P passing through a circle of radius r in the transverse plane at position z is
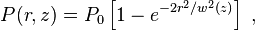
where
is the total power transmitted by the beam.
For a circle of radius
, the fraction of power transmitted through the circle is
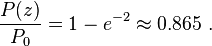
Similarly, about 95 percent of the beam's power will flow through a circle of radius
.[edit]Peak and average intensity
The peak intensity at an axial distance
from the beam waist is calculated using L'Hôpital's rule as the limit of the enclosed power within a circle of radius
, divided by the area of the circle
:
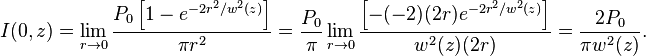
The peak intensity is thus exactly twice the average intensity, obtained by dividing the total power by the area within the radius
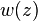.[edit]Derivation
The Gaussian beam formalism begins with the wave equation for an electromagnetic field in free space or in a homogeneous dielectric medium:[7]
where
may stand for any one of the six field components
,
,
,
,
, or
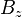. The Gaussian beam formalism proceeds by writing down a solution of the form[7]
where it is assumed that the beam is sufficiently collimated along the
axis that
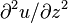may be neglected. Substituting this solution into the wave equation above yields the paraxial approximation to the wave equation:[7]
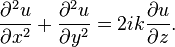
Solving this differential equation yields an infinite set of functions, of which the Gaussian beam is the lowest-order solution or mode.[edit]Higher-order modesSee also: Transverse mode
Gaussian beams are just one possible solution to the paraxial wave equation. Various other sets of orthogonal solutions are used for modelling laser beams. In the general case, if a complete basis set of solutions is chosen, any real laser beam can be described as a superposition of solutions from this set. The design of the laser determines which basis set of solutions is most useful. In some cases the output of a laser may closely approximate a single higher-order mode. Hermite-Gaussian modes are particularly common, since many laser systems have Cartesian reflection symmetry in the plane perpendicular to the beam's propagation direction.[edit]Hermite-Gaussian modes
Twelve Hermite-Gaussian modes
Hermite-Gaussian modes are a convenient description for the output of lasers whose cavity design is not radially symmetric, but rather has a distinction between horizontal and vertical. In terms of the previously defined complex
parameter, the amplitude distribution in the
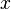-plane is proportional to
where the function
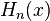is the Hermite polynomial of order
(physicists' form, i.e.
), and the asterisk indicates complex conjugation. For the case
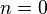the equation yields a Gaussian transverse distribution.
For two-dimensional rectangular coordinates one constructs a function
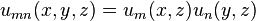, where
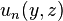has the same form as
. Mathematically this property is due to the separation of variables applied to the paraxial Helmholtz equation for Cartesian coordinates.[8]
Hermite-Gaussian modes are typically designated "TEMmn", where m and n are the polynomial indices in the x and y directions. A Gaussian beam is thus TEM00.[edit]Laguerre-Gaussian modes
The intensity profiles of twelve Laguerre-Gaussian modes
If the problem is cylindrically symmetric, the natural solutions of the paraxial wave equation are Laguerre-Gaussian modes. They are written in cylindrical coordinates using Laguerre polynomials
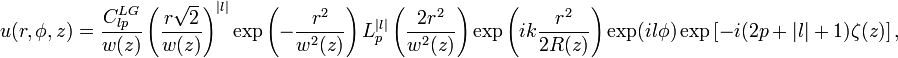
where
are the generalized Laguerre polynomials, the radial index
and the azimuthal index is
.
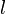is an appropriate normalization constant;
,
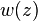and
are beam parameters defined above.[edit]Ince-Gaussian modes
In elliptic coordinates, one can write the higher-order modes using Ince polynomials. The even and odd Ince-Gaussian modes are given by [9]
where
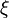and
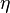are the radial and angular elliptic coordinates defined by
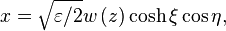
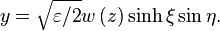
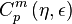are the even Ince polynomials of order
and degree
,
is the ellipticity parameter, and
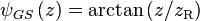is the Gouy phase. The Hermite-Gaussian and Laguerre-Gaussian modes are a special case of the Ince-Gaussian modes for
and
respectively.[edit]Hypergeometric-Gaussian modes
There is another important class of paraxial wave modes in polar coordinates in which the complex amplitude is proportional to a confluent hypergeometric function.
These modes have a singular phase profile and are eigenfunctions of the photon orbital angular momentum. The intensity profile is characterized by a single brilliant ring with a singularity at its center, where the field amplitude vanishes.[10]
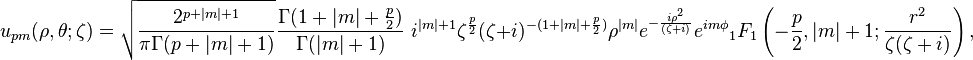
where
is integer,
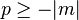is real valued,
is the gamma function and
is a confluent hypergeometric function.
Some subfamilies of hypergeometric-Gaussian (HyGG) modes can be listed as the modified Bessel-Gaussian modes, the modified exponential Gaussian modes, and the modified Laguerre–Gaussian modes.
The set of hypergeometric-Gaussian modes is overcomplete and is not an orthogonal set of modes. In spite of its complicated field profile, HyGG modes have a very simple profile at the pupil plane:
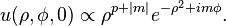
See Optical vortex, which explains that the outcoming wave from a pitch-fork hologram is a sub-family of HyGG modes. The HyGG profile while beam propagates along
has a dramatic change and it is not a stable mode below the Rayleigh range.
2099
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
