前言:本文内容来自学堂在线(xuetangX)的网络课程,代码为课件摘录,主要用于算法思路理解,未经过测试。欲完整了解,请前往网站免费学习(邓公的课超级好看,强烈推荐!!!)。
本文主要包含以下几种树结构:BST,AVL,伸展树,B树,红黑树
二叉树
BST 二叉搜索树:call-by-key:任一节点均不小于其左子树,不大于其右子树。(中序遍历必单调非降)
对于查找操作,如果没找到,内置变量_hot定位NULL位置的根部节点
对于插入操作,在底部插入
对于删除操作:如果该节点没有左子树或右子树,则直接删除该节点;否则,用后继节点交换该节点,删除后继节点位置。
最坏情况会退化为链表,引入以下BBST(平衡二叉搜索树)~~~
AVL树(Adelson-Velsky & E. Landis):平衡因子不大于1,即 balFac(v) = height(lc(v)) – height(rc(v)) <= 1
BST派生,严格控制树高。
理解插入节点,引起失衡,只导致一个父节点失衡;删除节点,引起失衡,会导致连串父节点失衡。
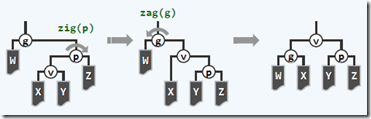
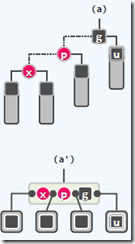
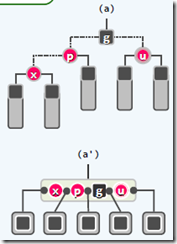
失衡调整:zig-zig, zig-zag, zag-zag, zag-zig, 以及3-4重构
优点:无论查找、插入、删除,最坏情况下复杂度均为O(logn),因为控制了树高嘛
缺点:不利于频繁插入删除操作
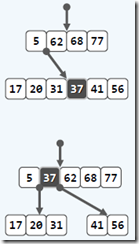
伸展树(Self-Adjusting Binary Tress):
BST派生,利用数据访问局部性,调整树结构,便于之后查找。
与AVL相比,更简单易行,且分摊复杂度为O(logn),与AVL相当。
精髓:向上追溯两层,而非一层,进行3-4重构。
优点:利用数据访问的局部性,查找效率自适应logK(常访问的伸展至根部);
缺点:不适合效率敏感的场合,不能杜绝单次最坏情况出现。
B树:平衡的多路搜索树
逻辑上和BBST完全等价,引入超级节点(每2代合并:4路,即4阶),为减少I/O次数(一次读多个数据或一个数据时间差不多)。目前数据库系统采用m=#keys/pg =200~300, 需要I/O次数log(m, n)。
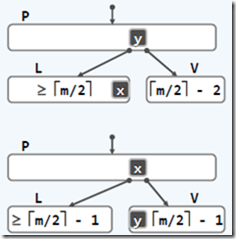
m阶B树【除根外,内部节点分支数不超过m,不少于ceiling(m/2),所有叶节点深度相等,树高对应外部节点】
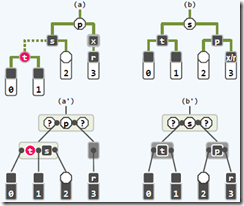
查找--插入(叶子)--上溢?--分裂【下图1】--根上溢?
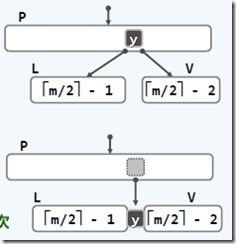
查找--删除(不一定叶子)--交换(变成叶子)--下溢?--旋转【下图2】/合并【下图3】—(合并时)根下溢?
B*树
从独自分裂到联合分裂,节点上溢时,由k个饱和的兄弟均摊新关键码,得到k+1个相邻节点,使空间使用率从50%提高到k/(k+1)
红黑树:由红、黑两类节点组成的BST
BST派生,四条规则(根必黑,外部节点必黑,不存在红红父子,外部节点到根途中黑节点数目相等)
目的:保持一致性结构,每次插入/删除后拓扑结构的变化不超过O(1),支持对历史版本访问?
对应4阶B树:红节点提升与一个黑节点组成超级节点。
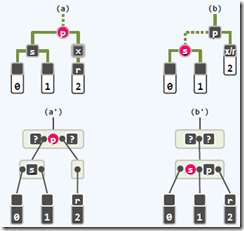
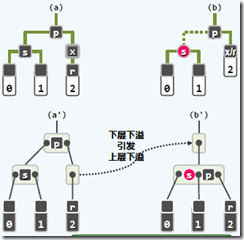
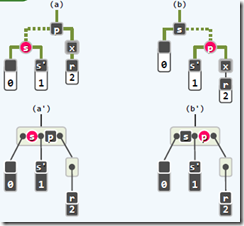
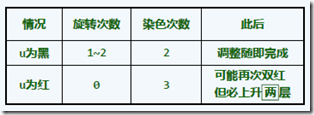
插入:首先视x为红节点(必在叶子中)--双红?(RR-1【下图1】 旋转,重染色并重构,终止递归,对应B树超级节点内部顺序不变)(RR-2【下图2】 只重染色,进行递归,对应B树发生上溢,递归g)
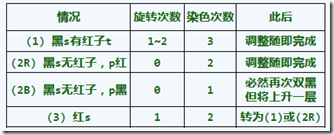
删除:待删除孩子x的后继节点r —若r为红色(x是黑的),直接变黑,保持规则。--若r为黑色,则观察兄弟s:s为黑且有红孩子(BB-1【下图1】,进行旋转,重染色,结束;对应B树从兄弟借);s为黑且无红孩子(此时p为红,定义BB-2R【下图2】,重染色,结束;对应B树与兄弟合并,父节点删除p,根必有一个黑色节点,因此不会下溢)(此时p为黑,定义BB-2B【下图3】,相对BB-2R,此时根节点可能下溢,重染色,递归上层下溢情况);s为红(BB-3【下图4】,此时s孩子必为黑,进行旋转,sp重染色后,转向BB-1或BB-2R情况,绝不会是BB-2B(因为p为红),递归;对应B树的超级节点内部结构不变)
特点:
每一次插入操作,最多O(logn)次节点染色,1次3-4重构
每一个删除操作,至多O(logn)次重染色,1次3-4重构,1次单旋。
代码


1 // 树节点定义 2 #define BinNodePosi(T) BinNode<T>* 3 template <typename T> struct BinNode { 4 BinNodePosi(T) parent; 5 BinNodePosi(T) lc; 6 BinNodePosi(T) rc; 7 T data; int height; int size(); 8 BinNodePosi(T) insertAsLC(T const &); 9 BinNodePosi(T) insertAsRC(T const &); 10 BinNodePosi(T) succ(); // 中序遍历意义下的后继节点 11 template <typename VST> void travLevel(VST &); 12 template <typename VST> void travPre(VST &); 13 template <typename VST> void travIn(VST &); 14 template <typename VST> void travPost(VST &); 15 }; 16 template <typename T> BinNodePosi(T) BinNode<T>::insertAsLC(T const &e) { 17 // 插入左叶子 18 return lc = new BinNode(e, this); 19 } 20 template <typename T> BinNodePosi(T) BinNode<T>::insertAsRC(T const &e) { 21 // 插入右叶子 22 return rc = new BinNode(e, this); 23 } 24 template <typename T> int BinNode<T>::size() { 25 // 统计后继节点个数 26 int s = 1; 27 if (lc) s += lc->size(); 28 if (rc) s += rc->size(); 29 return s; 30 }


1 // 二叉树定义 2 template <typename T> class BinTree { 3 protected: 4 int _size; 5 BinNodePosi(T) _root; 6 virtual int updateHeight(BinNodePosi(T) x); 7 void updateHeightAbove(BinNodePosi(T) x); 8 9 public: 10 int size() const { return _size; } 11 bool empty() const { return !_root; } 12 BinNodePosi(T) root() const { return _root; } 13 14 int remove(BinNodePosi(T) x); 15 BinTree<T>* secede(BinNodePosi(T) x); 16 BinNodePosi(T) insertAsLC(BinNodePosi(T) x, T const &e); 17 BinNodePosi(T) insertAsRC(BinNodePosi(T) x, T const &e); 18 BinNodePosi(T) attachAsRC(BinNodePosi(T) x, BinTree<T>* &S); 19 BinNodePosi(T) attachAsLC(BinNodePosi(T) x, BinTree<T>* &S); 20 }; 21 #define stature(p) ((p) ? (p)->height : -1) //空树高度为-1 22 template <typename T> int BinTree<T>::updateHeight(BinNodePosi(T) x) { 23 // 更新节点高度 24 return x->height = 1 + max(stature(x->lc), stature(x->rc)); 25 } 26 template <typename T> void BinTree<T>::updateHeightAbove(BinNodePosi(T) x) { 27 // 更新树高 28 while (x) { 29 updateHeight(x); x = x->parent; 30 } 31 } 32 template <typename T> BinNodePosi(T) BinTree<T>::insertAsRC(BinNodePosi(T) x, T const &e) { 33 // 添加右叶子 34 _size++; x->insertAsRC(e); 35 updateHeightAbove(x); 36 return x->rc; 37 } 38 template <typename T> BinNodePosi(T) BinTree<T>::insertAsLC(BinNodePosi(T) x, T const &e) { 39 // 添加左叶子 40 _size++; x->insertAsLC(e); 41 updateHeightAbove(x); 42 return x->lc; 43 } 44 template <typename T> BinNodePosi(T) BinTree<T>::attachAsRC(BinNodePosi(T) x, BinTree<T>* &S) { 45 // 添加右子树 46 if (x->rc = S->_root) x->rc->parent = x; // 注意,这里是= 不是== 47 _size += S->size; 48 updateHeightAbove(x); 49 S->_root = NULL; S->_size = 0; 50 releas(S); S = NULL; 51 return x; 52 } 53 template <typename T> BinNodePosi(T) BinTree<T>::attachAsLC(BinNodePosi(T) x, BinTree<T>* &S) { 54 // 添加左子树 55 if (x->lc = S->_root) x->lc->parent = x; 56 _size += S->size; 57 updateHeightAbove(x); 58 S->_root = NULL; S->_size = 0; 59 releas(S); S = NULL; 60 return x; 61 } 62 template <typename T> int BinTree<T>::remove(BinNodePosi(T) x) { 63 // 子树删除 64 FromParentTo(*x) = NULL; 65 updateHeightAbove(x->parent); 66 int n = removeAt(x); _size -= n; 67 return n; //返回被删除节点总数 68 } 69 template <typename T> static int removeAt(BinNodePosi(T) x) { 70 if (!x) return 0; 71 int n = 1 + removeAt(x->lc) + removeAt(x->rc); 72 release(x->data); release(x); return n; 73 } 74 template <typename T> BinTree<T>* BinTree<T>::secede(BinNodePosi(T) x) { 75 // 子树分离 76 FromParentTo(*x) = NULL; 77 updateHeightAbove(x->parent); 78 BinTree<T>* S = new BinTree<T>; 79 S->_root = x; x->parent = NULL: 80 S->_size = x->size(); _size -= S->_size; 81 return S; // 返回封装后的子树 82 } 83 template <typename T, typename VST> void traverse(BinNodePosi(T) x, VST & visit) { 84 // 双递归 先序遍历 85 if (!x) return; 86 visit(x->data); 87 traverse(x->lc, visit); 88 traverse(x->rc, visit); 89 } 90 template <typename T, typename VST> void travPre_I1(BinNodePosi(T) x, VST &visit) { 91 // 迭代+栈 先序遍历 92 Stack < BinNodePosi(T) > S; 93 if (x) S.push(x); 94 while (!S.empty()) { 95 x = S.pop(); visit(x->data); 96 if (HasRChild(*x)) S.push(x->rc); 97 if (HasLChild(*x)) S.push(x->lc); //左孩子后入先出 98 } 99 } 100 template <typename T, typename VST> void travPre_I2(BinNodePosi(T) x, VST &visit) { 101 // 迭代+栈(优化) 先序遍历 102 Stack <BinNodePosi(T)> S; 103 while (true) { 104 while (x) { 105 visit(x->data); 106 S.push(x->rc); 107 x = x->lc; 108 } 109 if (S.empty()) break; 110 x = S.pop(); 111 } 112 } 113 template <typename T, typename V> void travIn_I1(BinNodePosi(T) x, V &visit) { 114 // 迭代+栈(优化) 中序遍历 115 Stack < BinNodePosi(T)> S; 116 while (true) { 117 while (x) { 118 S.push(x); 119 x = x->lc; 120 } 121 if (S.empty()) break; 122 x = S.pop(); 123 visit(x->data); 124 x = x->rc; 125 } 126 } 127 template <typename T> BinNodePosi(T) BinNode<T>::succ() { 128 // 返回中序遍历意义上的后继节点 129 BinNodePosi(T) s = this; 130 if (rc) { 131 s = rc; 132 while (HasLChild(*s)) s = s->lc; // 可能是右子树的最左节点 133 } 134 else { 135 while (IsRChild(*s)) s = s->parent; // 也可能是当前节点包含于左子树中的最低祖先 136 s = s->parent; 137 } 138 return s; 139 } 140 template <typename T, typename VST> void travPost_I(BinNodePosi(T) x, VST &visit) { 141 // 迭代+栈 后序遍历 142 Stack<BinNodePosi(T)> S; 143 if (x) S.push(x); 144 while (!S.empty()) { 145 if (S.top() != x->parent) { // 栈顶非x之父,即为右兄,右子树入栈。 146 while (BinNodePosi(T) x = S.top()) 147 if (HasLChild(*x)) { 148 if (HasRChild(*x)) 149 S.push(x->rc); 150 S.push(x->lc); 151 } 152 else 153 S.push(x->rc); 154 S.pop(); // 弹出栈顶空节点 155 } 156 x = S.pop(); 157 visit(x->data); 158 } 159 } 160 template <typename T> template <typename VST> void BinNode<T>::travLevel(VST &visit) { 161 // 迭代+队列 层次遍历 162 Queue<BinNodePosi(T)> Q; 163 Q.enqueue(this); 164 while (!Q.emtpy()) { 165 BinNodePosi(T) x = Q.dequeue(); 166 visit(x->data); 167 if (HasLChild(*x)) Q.enqueue(x->lc); 168 if (HasRChild(*x)) Q.enqueue(x->rc); 169 } 170 }


1 // 二叉搜索树定义 2 template <typename T> class BST : public BinTree<T> { 3 public: 4 virtual BinNodePosi(T) & search(const T &); 5 virtual BinNodePosi(T) insert(const T &); 6 virtual bool remove(const T &); 7 protected: 8 BinNodePosi(T) _hot; // 查找时定位父节点 9 BinNodePosi(T) connect34( 10 BinNodePosi(T), BinNodePosi(T), BinNodePosi(T), 11 BinNodePosi(T), BinNodePosi(T), BinNodePosi(T), BinNodePosi(T)); 12 BinNodePosi(T) rotateAt(BinNodePosi(T)); 13 }; 14 template <typename T> BinNodePosi(T) & BST<T>::search(const T & e) { 15 // 查找节点 16 return searchIn(_root, e, _hot = NULL); 17 } 18 template <typename T> 19 static BinNodePosi(T) & searchIn(BinNodePosi(T) &v, const T &e, BinNodePosi(T) &hot) { 20 if (!v || e == v->data) return v; 21 hot = v; 22 return searchIn((e < v->data ? v->lc : v->rc), e, hot); // 若不存在,则v为null,hot为父节点 23 } 24 template <typename T> BinNodePosi(T) BST<T>::insert(const T &e) { 25 // 插入节点 26 BinNodePosi(T) & x = search(e); 27 if (!x) { 28 x = new BinNode<T>(e, _hot); 29 _size++; updateHeightAbove(x); 30 } 31 return x; 32 } 33 template <typename T> bool BST<T>::remove(const T &e) { 34 // 删除节点 35 BinNodePosi(T) & x = search(e); 36 if (!x) return false; 37 removeAt(x, _hot); 38 _size--; 39 updateHeightAbove(_hot); 40 return true; 41 } 42 template <typename T> static BinNodePosi(T) 43 removeAt(BinNodePosi(T) &x, BinNodePosi(T) &hot) { 44 BinNodePosi(T) w = x; // 定位实际要删除的位置 45 BinNodePosi(T) succ = NULL; //接替者,可能是中序遍历下后继节点,也可能是前继节点(无右子树) 46 if (!HasLChild(*x)) succ = x = x->rChild; 47 else if (!HasRChild(*x)) succ = x = x->lChild; 48 else { 49 w = w->succ(); swap(x->data, w->data); // succ() 找到后继,右子树最左边的节点 50 BinNodePosi(T) u = w->parent; 51 (u == x ? u->rc : u->lc) = succ = w->rc; // w肯定无左孩子,需改接w右子树 52 } 53 hot = w->parent; // 记录的删除位置的父节点(如果交换过,就是交换后的位置的父节点) 54 if (succ) succ->parent = hot; 55 release(w->data); releas(w); 56 return succ; // 返回接替者 57 } 58 template <typename T> BinNodePosi(T) BST<T>::connect34( 59 // 3-4重构 60 BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c, 61 BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3) { 62 a->lc = T0; if (T0) T0->parent = a; 63 a->rc = T1; if (T1) T1->parent = a; updateHeight(a); 64 c->lc = T2; if (T2) T2->parent = c; 65 c->rc = T3; if (T3) T3->parent = c; updateHeight(c); 66 b->lc = a; a->parent = b; 67 b->rc = c; c->parent = b; updateHeight(b); 68 return b; 69 } 70 template <typename T> BinNodePosi(T) BST<T>::rotateAt(BinNodePosi(T) v) { 71 // 调整平衡 72 BinNodePosi(T) p = v->parent, g = p->parent; 73 if (IsLChild(*p)) 74 if (IsLChild(*v)) { // zig-zig 75 p->parent = g->parent; 76 return connect34(v, p, g, v->lc, v->rc, p->rc, g->rc); 77 } 78 else { // zig-zag 79 v->parent = g->parent; 80 return connect34(p, v, g, p->lc, v->lc, v->rc, g->rc); 81 } 82 else { 83 /*.. zag-zig & zag-zag ..*/ 84 } 85 }


1 // AVL树定义(由BST派生) 2 #define Balanced(x) (stature( (x).lc) ) == stature( (x).rc )) // 理想平衡 3 #define BalFac(x) (stature( (x).lc ) - stature( (x).rc )) // 平衡因子 4 #define AvlBalanced(x) ((-2 < BalFac(x) ) && (BalFac(x) < 2)) // 平衡条件 5 template <typename T> class AVL : public BST<T> { 6 public: 7 BinNodePosi(T) insert(const T&); 8 bool remove(const T&); 9 }; 10 template <typename T> BinNodePosi(T) AVL<T>::insert(const T &e) { 11 // 插入节点,并调整平衡度,更新树高 12 BinNodePosi(T) &x = search(e); 13 if (x) return x; 14 BinNodePosi(T) xx = x = new BinNode<T>(e, _hot); _size++; 15 for (BinNodePosi(T) g = _hot; g; g = g->parent) 16 if (!AvlBalanced(*g)) { 17 FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g))); 18 break; //插入复原只一次,以上平衡度和树高均不再变化 19 } 20 else { 21 updateHeight(g); 22 } 23 return xx; 24 } 25 template <typename T> bool AVL<T>::remove(const T &e) { 26 // 删除节点 27 BinNodePosi(T) &x = search(e); 28 if (!x) return false; 29 removeAt(x, _hot); _size--; 30 for (BinNodePosi(T) g = _hot; g; g = g->parent) { 31 if (!AvlBalanced(*g)) { 32 g = FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g))); 33 } 34 updateHeight(g); // 可能调整logn次,树高均可能下降 35 } 36 return true; 37 }


1 // 伸展树定义 2 template <typename T> class Splay :pulbic BST<T> { 3 protected: BinNodePosi(T) splay(BinNodePosi(T) v); 4 public: 5 BinNodePosi(T) & search(const T &e); 6 BinNodePosi(T) insert(const T &e); // search 完成后,顶点附近插入 7 bool remove(const T &e); // search 完成后,顶点附近删除 8 }; 9 template <typename T> BinNodePosi(T) Splay<T>::splay(BinNodePosi(T) v) { 10 // 伸展算法 11 if (!v) return NULL; BinNodePosi(T) p; BinNodePosi(T) g; 12 while ((p = v->parent) && (g = p->parent)) { 13 // 先取下来,3-4重构完成后,再挂上去,直到挂到根 14 BinNodePosi(T) gg = g->parent; 15 if (IsLChild(*v)) 16 if (IsLChild(*p)) { /* zig-zig */ 17 attachAsLChild(g, p->rc); 18 attachAsLChild(p, v->rc); 19 attachAsRChild(p, g); 20 attachAsRChild(v, p); 21 } 22 else { /* zig-zag */ } 23 else if (IsRChild(*p)) { /* zag-zag */ } else { /* zag-zig */ }; 24 if (!gg) v->parent = NULL; 25 else (g == gg->lc) ? attachAsLChild(gg, v) : attachAsRChild(gg, v); 26 updateHeight(g); updateHeight(p); updateHeight(v); 27 } 28 if (p = v->parent) { /* 若p是根,再额外单旋至多一次 */; } 29 v->parent = NULL; return v; 30 } 31 template <typename T> BinNodePosi(T) &Splay<T>::search(const T &e) { 32 // 查找算法 33 BinNodePosi(T) p = searchIn(_root, e, _hot = NULL); 34 _root = splay(p ? p : _hot); // 无论是否找到,都splay至根 35 return _root; 36 }


1 // B树定义 2 #define BTNodePosi(T) BTNode<T>* 3 #define Rank int 4 template <typename T> struct BTNode { 5 BTNodePosi(T) parent; // 父 6 vector<T> key; // 数值向量 7 vector<BTNodePosi(T)> child; // 孩子向量 总比key多一 8 BTNode() { parent = NULL; child.insert(0, NULL); } 9 BTNode(T e, BTNodePosi(T) lc = NULL, BTNodePosi(T) rc = NULL) { 10 parent = NULL; 11 key.insert(0, e); 12 child.insert(0, lc); child.insert(1, rc); 13 if (lc) lc->parent = this; if (rc) rc->parent = this; 14 } 15 }; 16 template <typename T> class BTree { 17 protected: 18 int _size; int _order; BTNodePosi(T) _root; //关键码总数,阶次,根 19 BTNodePosi(T) _hot; // 查找访问的非空节点位置 20 void solveOverflow(BTNodePosi(T)); // 因插入而上溢后的分裂处理 21 void solveUnderflow(BTNodePosi(T)); // 因删除而下溢后的合并处理 22 public: 23 BTNodePosi(T) search(const T &); 24 bool insert(const T &); 25 bool remove(const T &); 26 }; 27 template <typename T> BTNodePosi(T) BTree<T>::search(const T &e) { 28 // 查找 29 BTNodePosi(T) v = _root; _hot = NULL; 30 while (v) { 31 Rank r = v->key.search(e); 32 if (0 <= r && e == v->key[r]) return v; // 返回所在节点的_root 33 _hot = v; v = v->child[r + 1]; // key[r] --> child[r+1] 34 } 35 return NULL; // 抵达外部节点,注意_hot记录的点位 36 } 37 template <typename T> bool BTree<T>::insert(const T &e) { 38 // 插入 39 BTNodePosi(T) v = search(e); 40 if (v) return false; 41 Rank r = _hot->key.search(e); 42 _hot->key.insert(r + 1, e); 43 _hot->child.insert(r + 2, NULL); 44 _size++; solveOverflow(_hot); 45 return true; 46 } 47 template <typename T> void BTree<T>::solveOverflow(BTNodePosi(T) v) { 48 if (_order >= v->child.size()) return; 49 Rank s = _order / 2; 50 BTNodePosi(T) u = new BTNode<T>(); // 分裂出右侧节点u 51 for (Rank j = 0; j < _order - s - 1; ++j) { 52 u->child.insert(j, v->child.remove(s + 1)); 53 u->key.insert(j, v->key.remove(s + 1)); 54 } 55 u->child[_order - s - 1] = v->child.remove(s + 1); 56 if (u->child[0]) // 更新u的孩子的父节点标记 57 for (Rank j = 0; j < _order - s; ++j) u->child[j]->parent = u; 58 BTNodePosi(T) p = v->paernt; // 把s位置孩子放至父节点p 59 if (!p) // 若父节点为空则增加一层 60 { 61 _root = p = new BTNode<T>(); p->child[0] = v; v->parent = p; 62 } 63 Rank r = 1 + p->key.search(v->key[0]); 64 p->key.insert(r, v->key.remove(s)); 65 p->child.insert(r + 1, u); u->parent = p; 66 solveOverflow(p); // 父节点p可能发生上溢 67 } 68 template <typename T> bool BTree<T>::remove(const T &e) { 69 // 删除 70 BTNodePosi(T) v = search(e); // 定位所在节点_root 71 if (!v) return false; 72 Rank r = v->key.search(e); // 定位所在位置 r 73 if (v->child[0]) { 74 BTNodePosi(T) u = v->child[r + 1]; // 定位后继节点(必是叶子) 75 while (u->child[0]) u = u->child[0]; 76 v->key[r] = u->key[0]; v = u; r = 0; // 用后继节点覆盖,删除此后继节点 77 } 78 v->key.remove(r); v->child.remove(r + 1); _size--; 79 solveUnderflow(v); // 可能发生下溢 80 return true; 81 } 82 template <typename T> void BTree<T>::solveUnderflow(BTNodePosi(T) v) { 83 if ((_order + 1) / 2 <= v->child.size()) return; 84 BTNodePosi(T) p = v->parent; // 定位父节点p 85 if (!p) { 86 } 87 Rank r = 0; while (p->child[r] != v) r++; 88 if (0 < r) {/* 情况1 若左兄弟存在,借借看? */ 89 BTNodePosi(T) ls = p->child[r - 1]; // 定位左兄弟ls 90 if ((_order + 1) / 2 < ls->child.size()) { // 可以借?旋转! 91 v->key.insert(0, p->key[r - 1]); 92 p->key[r - 1] = ls->key.remove(ls->key.size() - 1); 93 v->child.insert(0, ls->child.remove(ls->child.size() - 1)); 94 if (v->child[0]) v->child[0]->parent = v; 95 return; // 完成下溢处理 96 } 97 } 98 if (p->child.size() - 1 > r) { /* 情况2 考察右兄弟是否可借 类似情况1 */ } 99 if (0 < r) { /* 情况3 若左兄弟存在,与其合并 */ 100 BTNodePosi(T) ls = p->child[r - 1]; // 定位左兄弟ls 101 ls->key.insert(ls->key.size(), p->key.remove(r - 1)); // 父节点p中孩子r,左兄弟,v 合并 102 p->child.remove(r); 103 ls->child.insert(ls->child.size(), v->child.remove(0)); 104 if (ls->child[ls->child.size() - 1]) // 更新孩子父节点 105 ls->child[ls->child.size() - 1]->parent = ls; 106 while (!v->key.empty()) { 107 ls->key.insert(ls->key.size(), v->key.remove(0)); 108 ls->child.insert(ls->child.size(), v->child.remove(0)); 109 if (ls->child[ls->child.size() - 1]) 110 ls->child[ls->child.size() - 1]->parent = ls; 111 } 112 release(v); 113 } 114 else { /* 情况4 与右兄弟合并 类似情况3 */ } 115 solveUnderflow(p); // 情况3,4,检查父节点下溢情况 116 return; 117 }


1 // 红黑树定义 2 template <typename T> class RedBlack :public BST<T> { 3 public: 4 // BST::search()等其余接口可直接沿用 5 BinNodePosi(T) insert(const T &); // 插入(重写) 6 bool remove(const T &); // 删除(重写) 7 protected: 8 void solveDoubleRed(BinNodePosi(T) x); // 双红修正 9 void solveDoubleBlack(BinNodePosi(T) x); // 双黑修正 10 int updateHeight(BinNodePosi(T) x); // 更新节点高度,黑节点数量 11 }; 12 template <typename T> int RedBlack<T>::updateHeight(BinNodePosi(T) x) { 13 x->height = max(stature(x->lc), stature(x->rc)); 14 if (IsBlack(x)) x->height++; return x->height; 15 } 16 template <typename T> BinNodePosi(T) RedBlack<T>::insert(const T &e) { 17 BinNodePosi(T) &x = search(e); 18 if (x) return x; 19 x = new BinNode<T>(e, _hot, NULL, NULL, -1); _size++; // 创建[红]节点,以_hot为父,黑高度-1 20 solveDoubleRed(x); 21 return x ? x : _hot->parent; // 返回插入的节点 22 } 23 template <typename T> void RedBlack<T>::solveDoubleRed(BinNodePosi(T) x) { 24 if (IsRoot(*x)) { _root->color = RB_BLACK; _root->height++; return; } // 若是根直接转黑 25 BinNodePosi(T) p = x->parent; // 定位父节点 p 26 if (IsBlack(p)) return; 27 BinNodePosi(T) g = p->parent; // 父节点p为红,定位祖父 g(必为黑) 28 BinNodePosi(T) u = uncle(x); // 定位叔父 u ,叔父颜色决定了RR-1, RR-2 类型 29 if (IsBlack(u)) { /*.. 如果u为黑色或NULL RR-1 B树旋转,重染色并重构,终止递归 ..*/ 30 if (IsLChild(*x) == IsLChild(*p)) // 如果 x p 同侧, p g重染色;否则 x g重染色。 31 p->color = RB_BLACK; 32 else 33 x->color = RB_BLACK; 34 g->color = RB_RED; 35 BinNodePosi(T) gg = g->parent; // great-grand parent. 定位3-4重构的父节点 gg 36 BinNodePosi(T) r = FromParentTo(*g) = rotateAt(x); 37 r->parent = gg; 38 } 39 else { /*.. 如果u为红色 RR-2 B树发生上溢,只重染色,进行递归 ..*/ 40 p->color = RB_BLACK; p->height++; 41 u->color = RB_BLACK; u->height++; 42 if (!IsRoot(*g)) g->color = RB_RED; //B树角度:g插入上层超级节点,若非根则由黑转红 43 solveDoubleRed(g); 44 } 45 } 46 template <typename T> bool RedBlack<T>::remove(const T &e) { 47 BinNodePosi(T) &x = search(e); if (!x) return false; 48 BinNodePosi(T) r = removeAt(x, _hot); // 定位r,指向x接替者 49 if (!(--_size)) return true; // 如果删除后为空树? 50 if (!_hot) // 如果删除的是根,染黑,并更新黑高度 51 { 52 _root->color = RB_BLACK; updateHeight(_root); return true; 53 } 54 if (BlackHeightUpdated(*_hot)) return true; // 如果删除的非根,但不失衡 55 // 以下则黑高度失衡 56 if (IsRed(r)) { r->color = RB_BLACK; r->height++; return true; } // 接替者为红,直接转黑 57 solveDoubleBlack(r); return true; 58 } 59 template <typename T> void RedBlack<T>::solveDoubleBlack(BinNodePosi(T) r) { 60 BinNodePosi(T) p = r ? r->parent : _hot; if (!p) return; // 定位 r父节点 p 61 BinNodePosi(T) s = (r == p->lc) ? p->rc : p->lc; //定位 r兄弟 s 62 if (IsBlack(s)) { 63 BinNodePosi(T) t = NULL; // 定位兄弟s的红孩子,左者优先 64 if (IsRed(s->rc)) t = s->rc; 65 if (IsRed(s->lc)) t = s->lc; 66 if (t) { /* 黑s有红孩子,BB-1 对应B树向左兄弟借一个 */ 67 RBColor oldColor = p->color; 68 BinNodePosi(T) b = FromParentTo(*p) = rotateAt(t); 69 if (HasLChild(*b)) 70 { 71 b->lc->color = RB_BLACK; updateHeight(b->lc); 72 } 73 if (HasRChild(*b)) 74 { 75 b->rc->color = RB_BLACK; updateHeight(b->rc); 76 } 77 b->color = oldColor; updateHeight(b); 78 } 79 else { /* 黑s无红孩子,BB-2R或BB-2B 对应B树合并 */ 80 s->color = RB_RED; s->height--; 81 if (IsRed(p)) // BB-2R 82 { 83 p->color = RB_BLACK; 84 } 85 else // BB-2B 86 { 87 p->heigh--; solveDoubleBlack(p); 88 } 89 } 90 } 91 else { /* 红s,BB-3 */ 92 s->color = RB_BLACK; p->color = RB_RED; 93 BinNodePosi(T) t = IsLChild(*s) ? s->lc : s->rc; 94 _hot = p; FromParentTo(*p) = rotateAt(t); 95 solveDoubleBlack(r); 96 } 97 }




















 416
416











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








