量子叠加态系数_面向CS背景的量子计算入门介绍

本文原发于 如何用 IT 业者能听懂的话介绍量子计算的原理？ ，不知道是因为问题实在太老了还是新号没人权，只有几十的阅读量。虽然是一时上头写的，但是毕竟写了这么长不想浪费，所以就以文章的形式再发一次。

写这篇的起因是发现是知乎上的现有科普都“太物理”了，而且往往罗列了很多概念但是并没有完整地陈述任何算法，我想可能后者是计算机/数学背景者更想听的，所以着重做点补充。

当然，这可能主要是因为目前国内除了应组基本上都是物理背景为主，知乎上量子方面的大V也都基本都是物理背景。但既然近些年的趋势是越来越侧重量子计算，一份针对CS背景、跳过物理实现直接从数学抽象入手的入门介绍，应该是有价值的。

本文只是一份并不完整的粗浅解读，但是不需要任何物理背景，也不去谈各种高大上的概念，侧重于具体的计算模型和简单的算法例子，感兴趣的话可以拿起笔跟着一步步推下去。希望能帮助计算机/数学背景者对量子计算有个大概的了解。欢迎指正。

可以这么理解，量子计算能加速的本质在于其自带一定的叠加性。经典计算机上计算1+2和5+8需要调用两次加法器分别计算1+2=3和5+8=13，而量子计算机上输入“1叠加5”和“2叠加8”，调用一次量子加法器就可以得到“3叠加13”。

当然，我们并不能直接在“3叠加13”中获取到3和13这两个信息。但是凭借巧妙的设计，有些时候通过叠加态就能直接得到我们需要的结果。

---

（本文只讨论纯态pure state。本文主要介绍通用量子计算。）

经典计算机中每个比特要么是0要么是1，而量子计算机中对应的是

和

。

这里是狄拉克符号，对应的矩阵就是

。暂时不需要了解背后的物理含义，只需要知道这是对每个量子比特(qubit)的描述。就像经典计算机中我们也不需要了解0、1背后的高低电位。

不同于经典计算机中每个比特要么是0要么是1，量子计算机中每个qubit可能是0和1的叠加态，例如

,这两个系数都是复数且

。矩阵表示就是

。

这里说几个常用的记法，

。

---

经典计算机中当然是要用到很多比特的，量子计算机中一个系统同样有很多qubit。我们直接使用张量积(tensor product)连接。例如一个两qubit的系统，第一个qubit是

，第二个也是

，那么整个系统就直接描述为

，简写为

。对应的矩阵是

。

个qubit的系统(纯态)对应

的矩阵。

注意多个qubit同样有叠加态，例如：

，

又例如：

。

可能你已经注意到了，对两qubit的系统来说，这个矩阵的四个系数对应的就是

的系数。

（感兴趣可以去具体看一下tensor product具体的运算规则，不过这个不影响对后文的理解）

---

经典计算机中有与或非等各种门，量子计算机同样需要各种门(gate)来进行计算(again,跳过背后的物理意义)。一个作用在n位量子比特上的门描述为一个

的酉矩阵 (Unitary matrix)。比如著名的H门，

，不难验算

（也就是

）。再比如X门，使01翻转，

。

关于各种常见的门，参考维基百科就好了。

https://en.wikipedia.org/wiki/Quantum_logic_gate​en.wikipedia.org en.wikipedia.org​en.wikipedia.org

我们一般使用量子线路(circuit)来描述量子计算。

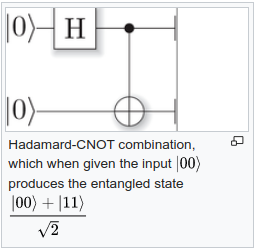
例如维基上这个例子，先经过H门，再经过CNOT门。不难验算，输入

则输出

。

写得更容易看懂一点就是：

。这里

可以理解为一个什么都没干的门，对应的就是单位矩阵

。

---

最后，关于测量，就是把量子信息再转化为经典信息。比如一qubit的态

,我们在

下去测量的话，就会以

的概率得到0，以

的概率得到1。

可能你已经注意到了，就测量的表现而言，我们并不能区分

和

，即使后续还有各种运算也无法区分。更一般的，

是无法被区分的，视为同一个态。这个系数被称为overall phase，可以忽略。

（注意一定要overall才能忽略，

和

显然并不能视为同一个东西）

---

---

有了上面这些铺垫，相当于我们已经理解了经典计算机中什么是0,什么是1，什么是运算，可以开始看具体的算法了。

Deutsch Algorithm

先看一个玩具问题。我有一个黑盒函数

。也就是说，输入输出都是1比特。现在我希望知道

是否相等，而且希望尽量少地调用

函数。（比如说，

是个很长很长的加密函数，跑一次要很久，而且很难直接分析数学性质）

不难看出最少需要两次，

和

各计算一次看看一不一样就好了。有没有可能只调用一次呢？至少经典计算机上是不可能的。

那么来看量子。

函数显然需要换成量子版本，

满足：

，其中

。不难验证这个矩阵是Unitary的。（这里不讨论

具体怎么实现，但不难想象，既然

函数能在经典计算机上实现，

对应的量子电路也能相应地搭出来）

既然要发挥量子计算机的威力，自然要输入叠加态。

先注意一个有趣的现象，计算

（也就是

），其结果恰好为

。

于是我们把

和

的情况叠加起来。

输入

（也就是

）,当

的时候，最终的结果为

；当

的时候，最终结果为

。

所以，我们只需要测量第一个qubit是

还是

（等价地，过一个

门然后测量是

还是

），就可以判断

是否相等了。

相比经典计算机调用了两次

，量子算法只需要调用一次

。

---

Deutsch-Jozsa Algorithm

这次稍微扩展一下：我有一个黑盒函数

。它满足：要么是“一致的”，也就是不管是输入什么，输出都一样；要么是“平衡的”，也就是

个输入中，恰好一半输入0，一半输入1。现在我希望尽量少地调用

函数，就判断出究竟是哪种情况。

不难看出，使用经典计算机，最坏情况需要调用

次，才能判断出究竟是“一致的”还是“平衡的”。

接下来考虑使用量子计算机。

函数需要换成量子版本，

满足：

。其中x、y分别是长度为

和

的01串。不难验证这个矩阵是Unitary的。（这里不讨论

具体怎么实现，但不难想象，既然

函数能在经典计算机上实现，

对应的量子电路也能相应地搭出来）

要判断究竟是“一致的”还是“平衡的”最少需要调用多少次

呢？

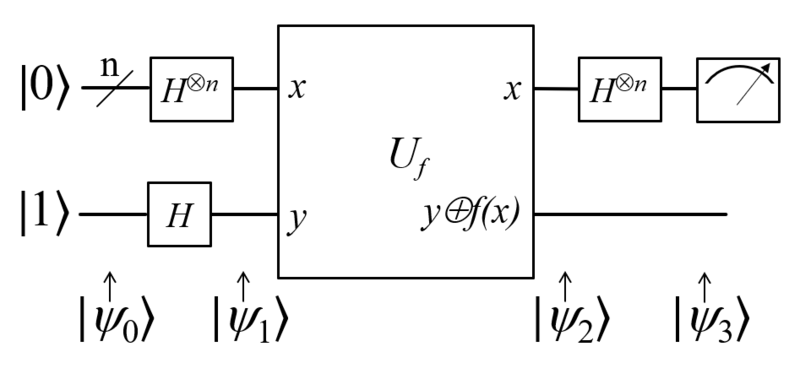
这次给出完整步骤：

输入是

个0和一个1（其实更常见的写法应该是从

个0开始，最后一位来个

门，不过无所谓了）

第一步，通过若干

门把

全部变成

,打开括号其实也就得到了

。

第二步，过

门，注意上面说的那个“有趣的现象”。

第三步，再给前

个qubit都过一遍

门。这里有另外一个“有趣的现象”，

。这个也可以直观理解，

的每一位都过一个

门，变成

，具体是正是负取决于对应的

是0还是1。打开括号，那么不难验证最终结果里面的

这一项的系数是正是负取决于把所有

异或起来（因为当且仅当

的时候会产生一个负号）。

这个时候来看最终的表达式，每一个

的系数为

。

如果

是“一致的”，那么

也是个常量，可以提到求和符号外面去。显然当且仅当

的时候整个表达式不为0（否则

总可以两两抵消）。换言之，最后得到的态就是

。

如果

是“平衡的”，那么在第二部以后恰好一半系数是+1一半是-1，这个态和系数全部+1的

是正交的（内积为0），所以第三步以后的态和

是正交的。换言之，最后得到的态里没有

这一项。

上面分析了这么多，实际做的时候反倒很简洁：

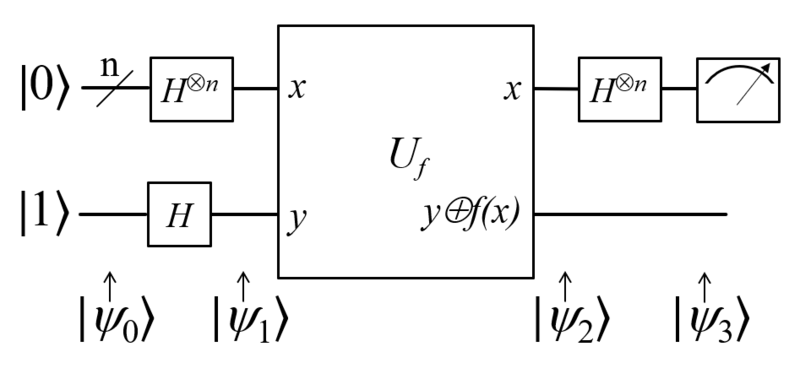
过

门，过

，再过

门，测量前n个qubit，如果测量结果都是0，“一致的”，否则“平衡的”。

对比一下，经典计算机下，最坏需要调用

次

，才能判断出究竟是“一致的”还是“平衡的”。而量子计算下只需要调用1次

。

---

通过这两个看起来没什么用，其实真的也没什么用的算法，应该可以感受到量子计算机超越经典计算机的威力。

【全文完】