hdu2586&&poj1330 求点间最短距&&最近公共祖先（在线&&离线处理）：：：可做模板...

最新推荐文章于 2024-11-15 18:38:47 发布

weixin_30376163

最新推荐文章于 2024-11-15 18:38:47 发布

阅读量109

点赞数

文章标签： java

原文链接：http://www.cnblogs.com/13224ACMer/p/4769681.html

版权

How far away ？

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 9097 Accepted Submission(s): 3171

Problem Description

There are n houses in the village and some bidirectional roads connecting them. Every day peole always like to ask like this "How far is it if I want to go from house A to house B"? Usually it hard to answer. But luckily int this village the answer is always unique, since the roads are built in the way that there is a unique simple path("simple" means you can't visit a place twice) between every two houses. Yout task is to answer all these curious people.

Input

First line is a single integer T(T<=10), indicating the number of test cases.
For each test case,in the first line there are two numbers n(2<=n<=40000) and m (1<=m<=200),the number of houses and the number of queries. The following n-1 lines each consisting three numbers i,j,k, separated bu a single space, meaning that there is a road connecting house i and house j,with length k(0<k<=40000).The houses are labeled from 1 to n.
Next m lines each has distinct integers i and j, you areato answer the distance between house i and house j.

Output

For each test case,output m lines. Each line represents the answer of the query. Output a bland line after each test case.

Sample Input

2

3 2

    1 2 10 
  

    3 1 15 
  

1 2

2 3

2 2

    1 2 100 
  

1 2

2 1

Sample Output

    10 25 100 100 
  

Source

ECJTU 2009 Spring Contest

描述:

已知在一个村庄中有n个房子，一些双向的道路把这些房子连接了起来。但是每天都有人询问诸如“如果我想从A房子走到B房子需要走多远的距离？” 的问题。幸运的是，在这个村庄中这个答案总是唯一的，因为任意两个房子之间仅存在一条简单路径（路径上的地点只能访问一次）。你现在的任务是回答这些人的询问。

输入：

输入一个整数n表示房子总数，一个整数m表示询问的总数（n<=40000,m<=200）,接下来的n-1行输入n-1条道路的状况，每行3个整数a，b，c表示a房子和b房子之间有一条长度为c的双向道路，接下来输入m行询问，每行两个整数a，b要求给出a房子和b房子的最小距离。

思路：可以用LCA算法计算出任意两个房子u,v的最近公共祖先lca(u,v)

假设d[]数组为每个房子节点到根节点的距离，那么有

dis(u, v) = d[u] + d[v] – 2*d[lca(u, v)]

在线算法

    /*
    这个版本的在线算法比自创的好看简洁多了，可以当模板，效率不高在于算法其本身的原因；
    据说离线算法要快不少。
    */
    #include <cstdio>
    #include <cstring>
    #include <iostream>
    #include <cmath>
    #include <vector>
    using namespace std;

    const int NN=50000;

    int n,rt;
    vector<pair<int,int> > edge[NN];

    int depth=0;
    int bn=0,b[NN*2]; //深度序列
    int f[NN*2];          //对应深度序列中的结点编号
    int p[NN];             //结点在深度序列中的首位置
    int dis[NN];          //结点到根的距离
    void dfs(int u,int fa)
    {
        int tmp=++depth;
        b[++bn]=tmp; f[tmp]=u; p[u]=bn;
        for (int i=0; i<edge[u].size(); i++)
        {
            int v=edge[u][i].first;
            if (v==fa) continue;
            dis[v]=dis[u]+edge[u][i].second;
            dfs(v,u);
            b[++bn]=tmp;
        }
    }

    int dp[NN*2][20];
    void rmq_init(int n) //以深度序列做rmq
    {
        for (int i=1; i<=n; i++) dp[i][0]=b[i];
        int m=floor(log(n*1.0)/log(2.0));
        for (int j=1; j<=m; j++)
          for (int i=1; i<=n-(1<<j)+1; i++)
              dp[i][j]=min(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
    }
    int rmq(int l,int r)
    {
        int k=floor(log((r-l+1)*1.0)/log(2.0));
        return min(dp[l][k],dp[r-(1<<k)+1][k]);
    }

    int lca(int a,int b)
    {
        if (p[a]>p[b]) swap(a,b);
        int k=rmq(p[a],p[b]);
        return f[k];
    }

    int main()
    {
        int m,u,v,w;
        int t;
        scanf("%d",&t);
        while(t--){
        scanf("%d%d",&n,&m);
        for (int i=1; i<=n; i++) edge[i].clear();
        for(int i=1;i<n;i++)
        {
            scanf("%d%d%d",&u,&v,&w);
            edge[u].push_back(make_pair(v,w));
            edge[v].push_back(make_pair(u,w));
        }
        rt=1; dis[rt]=0;
        dfs(1,0);
        rmq_init(bn);

        while (m--)
        {
            scanf("%d%d",&u,&v);
            printf("%d\n",dis[u]+dis[v]-2*dis[lca(u,v)]);
        }

        }
        return 0;
    }

离线算法

#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;

const int NN=50010;

int n,m;
vector<pair<int,int> > edge[NN],qe[NN];
vector<int> q1,q2;

int p[NN];
int find(int x)
{
    if (p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

int sum=0,ans[NN],dis[NN];
bool vis[NN]={0};
void lca(int u,int fa)
{
    p[u]=u;
    for (int i=0; i<edge[u].size(); i++)
    {
        int v=edge[u][i].first;
        if (v==fa) continue;
        dis[v]=dis[u]+edge[u][i].second;
        lca(v,u);
        p[v]=u;
    }
    vis[u]=true;
    if (sum==m) return;
    for (int i=0; i<qe[u].size(); i++)
    {
        int v=qe[u][i].first;
        if (vis[v])
            ans[qe[u][i].second]=dis[u]+dis[v]-2*dis[find(v)];
    }
}

int main()
{
    int u,v,w;

    int t;
    scanf("%d",&t);
    while(t--){
    scanf("%d%d",&n,&m);
    for (int i=1; i<=n; i++)
    {
        edge[i].clear();
    }
    for (int i=1; i<n; i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        edge[u].push_back(make_pair(v,w));
        edge[v].push_back(make_pair(u,w));
    }

    for (int i=0; i<m; i++)
    {
        scanf("%d%d",&u,&v);
        qe[u].push_back(make_pair(v,i));
        qe[v].push_back(make_pair(u,i));
        ans[i]=0;
    }
    dis[1]=0;
    lca(1,0);
    for (int i=0; i<m; i++) printf("%d\n",ans[i]);
    }
    return 0;
}

Nearest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 22116		Accepted: 11566

Description

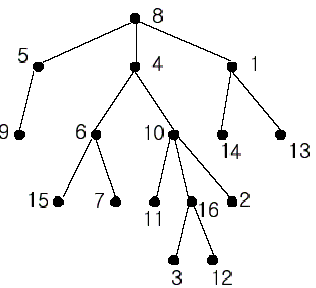
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:

In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.

Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

Sample Output

4
3

Source

Taejon 2002

//这个tarjan算法使用了并查集+dfs的操作。中间的那个并查集操作的作用，只是将已经查找过的节点捆成一个集合然后再指向一个公共的祖先。另外，如果要查询LCA(a,b)，必须把(a,b)和(b,a)都加入邻接表。
//
//O(n+Q)

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>

using namespace std;

#define MAXN 10001

int n,fa[MAXN];
int rank[MAXN];
int indegree[MAXN];
int vis[MAXN];
vector<int> hash[MAXN],Qes[MAXN];
int ances[MAXN];//祖先


void init(int n)
{
    for(int i=0;i<=n;i++)
    {
        fa[i]=i;
        rank[i]=0;
        indegree[i]=0;
        vis[i]=0;
        ances[i]=0;
        hash[i].clear();
        Qes[i].clear();
    }
}

int find(int x)
{
    if(x != fa[x])
        fa[x]=find(fa[x]);
    return fa[x];
}

void unio(int x,int y)
{
    int fx=find(x),fy=find(y);
    if(fx==fy) return ;
    if(rank[fy]<rank[fx])
        fa[fy]=fx;
    else
    {
        fa[fx]=fy;
        if(rank[fx]==rank[fy])
            rank[fy]++;
    }
}

void Tarjan(int u)
{
    ances[u]=u;
    int i,size = hash[u].size();
    for(i=0;i<size;i++)
    {
        Tarjan(hash[u][i]);//递归处理儿子
        unio(u,hash[u][i]);//将儿子父亲合并，合并时会将儿子的父亲改为u
        ances[find(u)]=u;//此时find(u)仍为u,即
    }
    vis[u]=1;

    //查询
    size = Qes[u].size();
    for(i=0;i<size;i++)
    {
        if(vis[Qes[u][i]]==1)//即查询的另一个结点开始已经访问过，当前的u在此回合访问。
        {
            printf("%d\n",ances[find(Qes[u][i])]);//由于递归，此时还是在u
            return;
        }
    }
}

int main()
{
    int t;
    int i,j;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        init(n);
        int s,d;
        for(i=1;i<=n-1;i++)
        {
            scanf("%d%d",&s,&d);
            hash[s].push_back(d);
            indegree[d]++;
        }
        scanf("%d%d",&s,&d);
    //    if(s==d)//如果需要计数的时候注意
//            ans[d]++;
//        else
//        {
            Qes[s].push_back(d);
            Qes[d].push_back(s);
//        }
        for(j=1;j<=n;j++)
        {
            if(indegree[j]==0)
            {
                Tarjan(j);
                break;
            }
        }
    }
    return 0;
}