定义:设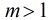
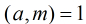

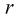
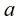

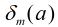
定理:如果模
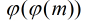
定理:若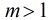
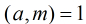
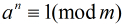
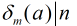
定理:如果


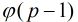
定理:设



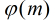


假设一个数

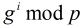
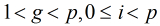


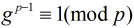


模
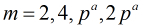
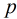
求模素数

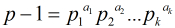

成立,则

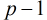
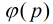
·定义 设m>1的整,g是其一个原根,(a,m)=1,则存在唯一整数r使 g^r三a (mod m) 则r叫做以g为底的a对模m的一个指标,记为r=ind g (a)。
注:性质类似指数、对数,所以有的人将这个称为指数。
2016-09-05 20:13:14
定义:设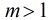
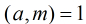

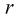
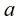

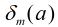
定理:如果模
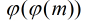
定理:若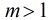
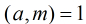
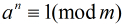
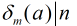
定理:如果


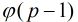
定理:设



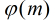


假设一个数

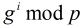
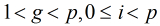


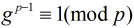


模
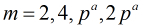
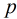
求模素数

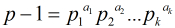

成立,则

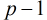
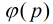
·定义 设m>1的整,g是其一个原根,(a,m)=1,则存在唯一整数r使 g^r三a (mod m) 则r叫做以g为底的a对模m的一个指标,记为r=ind g (a)。
注:性质类似指数、对数,所以有的人将这个称为指数。
2016-09-05 20:13:14
转载于:https://www.cnblogs.com/Konjakmoyu/p/5843464.html

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


