正三角形旋转一周得到的图形是_第一章《丰富的图形世界》回顾与思考

一、教学目标

1、鼓励学生自己梳理所学的内容，并力图在不同内容之间寻找联系。因此本节课应以学生小组活动为主，尽可能让他们在反思和交流的过程中，逐步建立知识体系。

2、在学生充分交流后，教师引导学生建立本章知识体系框架图。

3、本章主要内容围绕常见几何体展开。包括简单几何体的特征以及依据这些特征进行的分类，从不同的角度(不同方向看)，利用不同的方式(展开与折叠、切割)，研究简单几何体的某些特征，研究组成几何体的基本元素(点、线、面)间的相互关系。

二、复习回顾

1、依次回忆各节学习内容，两人一组，回答下列问题：

(1)生活中有哪些常见的几何体？请举列说明.

(2)棱柱、圆柱、圆锥的特征分别是什么？从哪些方面来描述？

(3)你能列举哪些点动成线、线动成面、面动成体的实例？

(4)找出两种几何体，使得分别用一个平面去截他们，可以得到三角形形状的截面。

(5)举出一种几何体，使得从正面、左面、上面看到的这个几何体的形状图都一样，你能举出几种？

2、引导学生交流以上问题，教师在黑板上适当的位置写下相应的知识点。

注意，这里不仅仅是理论的说明，教师应根据情况应该让学生进行一定的解释和举例说明。

3、进一步提问：这些知识之间有什么样的联系？能否用适当的符号，将这些关系表示出来。同时，在黑板上进行适当的标注。

4、通过上述步骤，在黑板上形成一个全章的知识框架图。教师分析这个框架图，并解释其中较为重要的知识点、考察点。同时，在设计例题时，也考虑与这些考察点相对应。

下面是本章知识体系的一个参考框图：

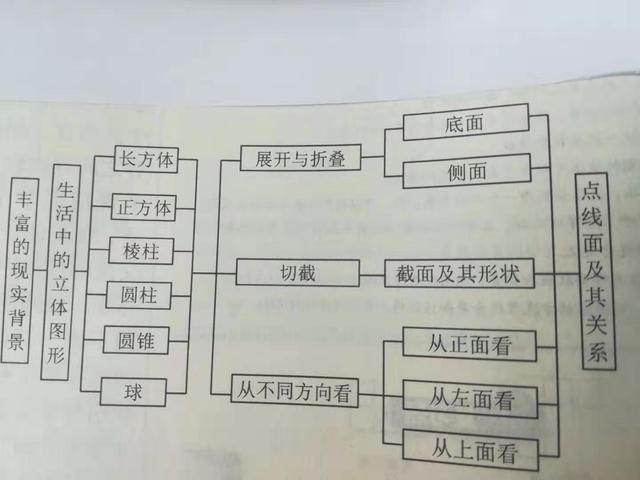
《丰富的图形世界》知识框架图

三、例题

例1、将下图中的几何体进行分类，并说明它们是由哪些面围城的。

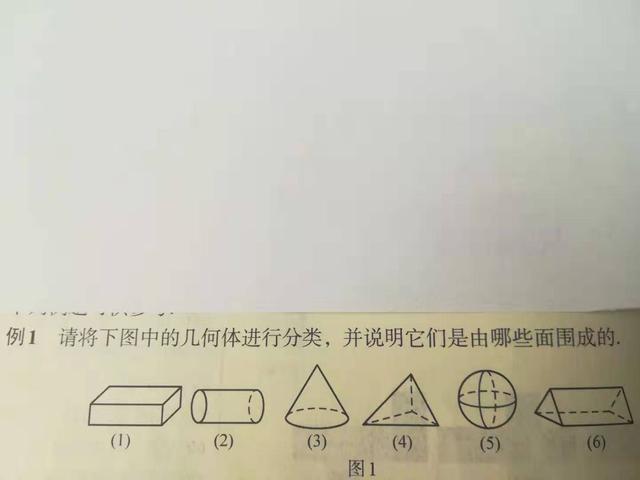
例1 图

分析：将几何体分类，方法并不唯一，只要能说明分类的理由即可。但要注意：按某一标准分类时要做到不重不漏。分类标准不同时，分类的结果也不尽相同。

答：按照柱体、椎体、球体分类：(1)、(2)、(6)是柱体；(3)、(4)是椎体；(5)是球体。

若按多面体(各个面由平面图形组成)、旋转体(由平面图绕某条直线形旋转而成)分：(1)、(4)、(6)是多面体；(2)、(3)、(5)是旋转体。

例2、用一个平面去截一个正方体，如果截去的几何体是一个三棱锥，那么

(1)截面一定是什么图形？

(2)剩下的几何体可能有几个顶点？

解：(1)如果截去的几何体是一个三棱锥，那么截面一定是一个三角形。

(2)如图所示，剩下的几何体可能有7个，8个，9个，10个顶点。

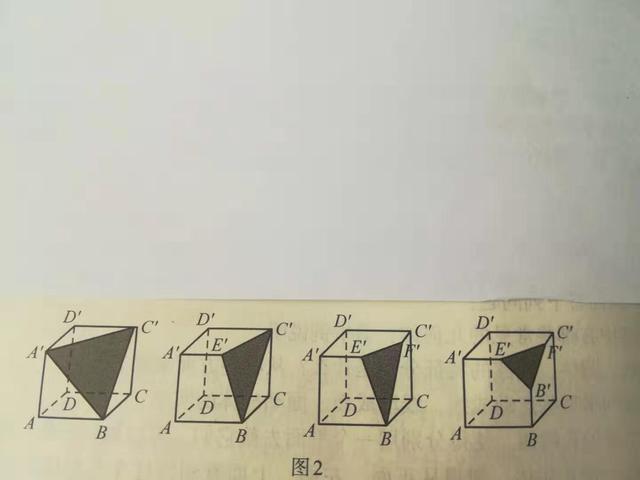
例2 解答图

本题具有一定的开放性，对于七年级学生来说具有很强的挑战性，解题的关键在于抓住“截面为三角形“这一特点，由此可联想到上述图中各种不同情况。

例3、将一个直角三角形ABC绕它的一边旋转，试画出旋转后所得到的几何体。

分析：由于题目中没有说明绕哪条边旋转，所以必须分三种情况考虑，得到三个不同的几何体。

解：如图，分别绕三条边旋转一周，得到三个几何体。

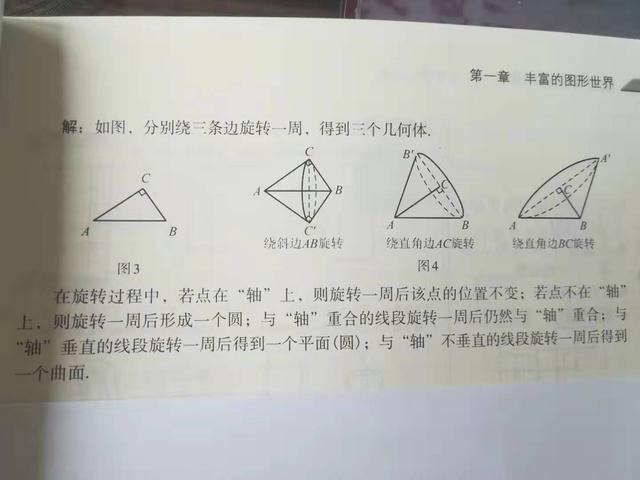
例3题解

四、复习题

第1题

答：1、由4个面围成；面与面相交成6条线，其中4条是直的，2条是曲的。

第2题平面图

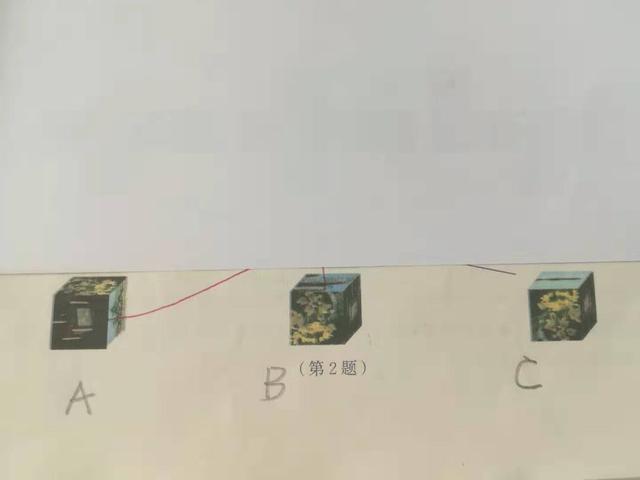
第2题围成的几何体

答：2、平面图中的(1)、(2)、(3)，分别对应着折成后的C、B、A。

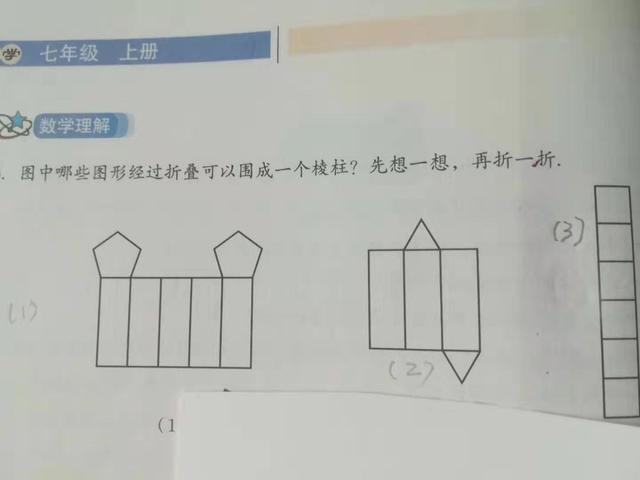
第3题

答：(1)不可以；(2)可以；(3)不可以

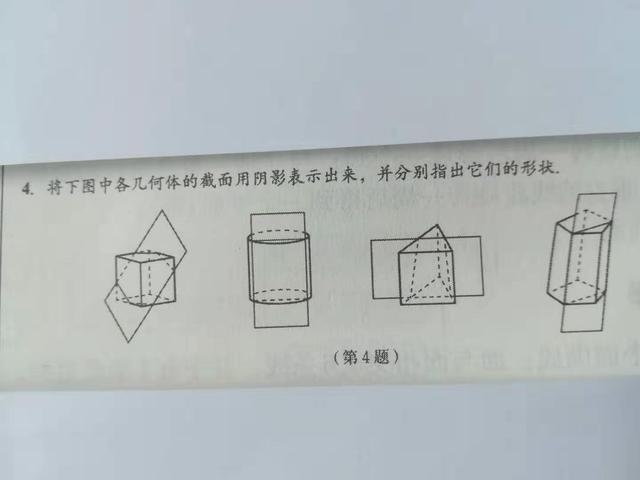
第4题

答：形状顺次为六边形，长方形，梯形、平行四边形。

5、6、7、8题和图

解：5，可以，可以

解：6，7题，如图所示

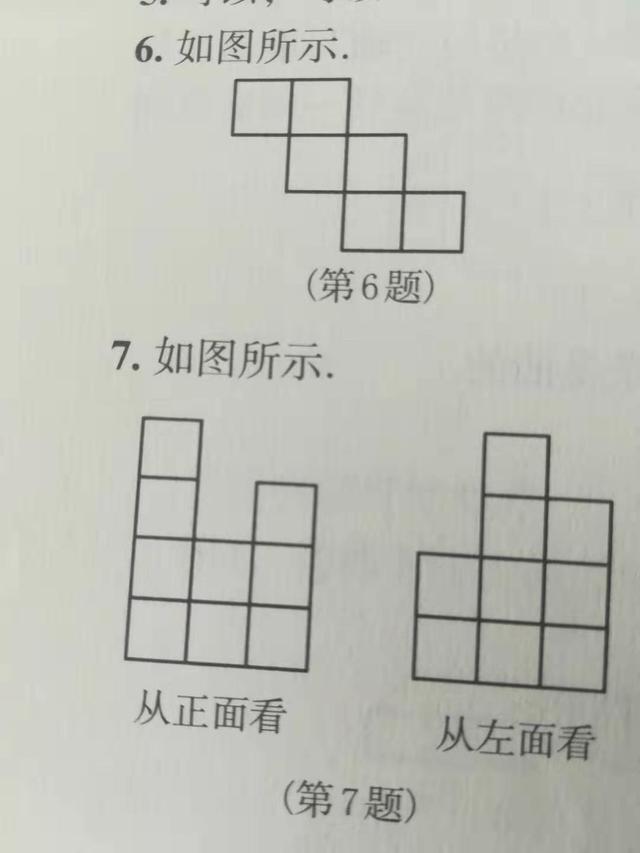
6题 7题答案

解：8、对于由大小相同的小立方块搭成的几何体来说，从正面、上面、左面看到两个不同的几何体时，看到的形状图有可能是相同的。

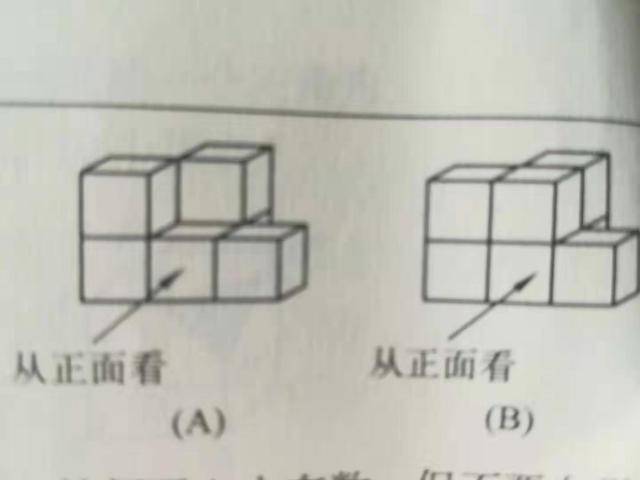
第8题举例

例如从正面、上面、左面上面两个几何体时，看到的形状图都相同，但显然这两个几何体的形状并不相同。几何体(A)由6个小立方块组成，而几何体(B)由7个小立方块组成.

出现这种情况与形状图的画法有关，如画形状图时用实线画出了每个小正方形的轮廓线，这一点与正规三视图是有区别的。(对此教师要心中有数，但不要向学生讲解)。

本题的答案有多种，从左面看到的形状图，可能有以下几种：

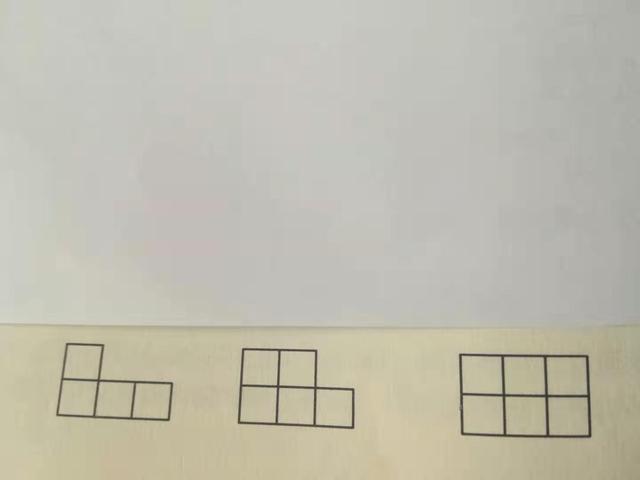
第8题答案

第9、10、11题

第9题答案：45乘以圆周率，单位：立方米。

解10：共8种。学生列出几种即可。

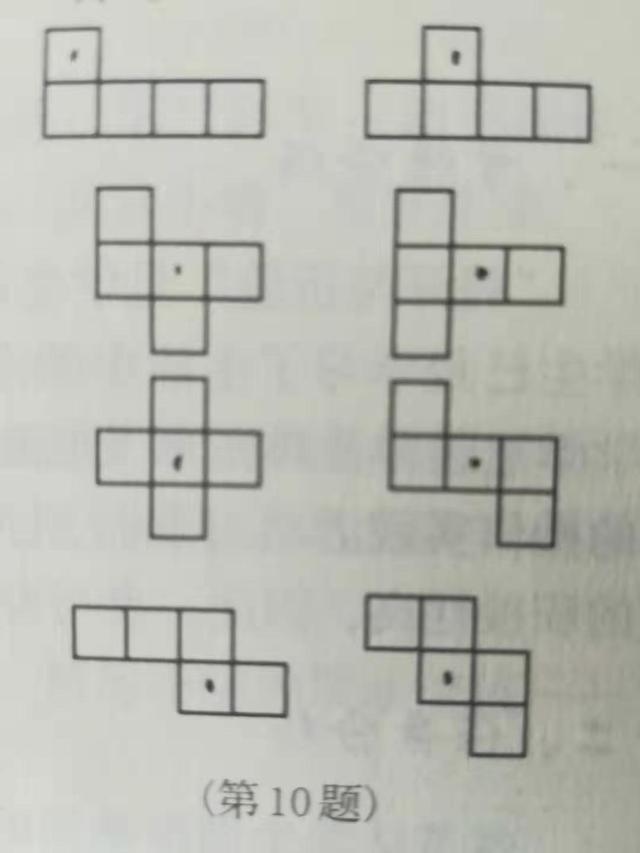
第10题答案

联系拓广第11题，解答：参考例3，是例3中的“绕斜边AB旋转“而成的几何体。

五、课堂小结：第一章内容讲完，同学们可以在课本学好的基础上，再做一下对应的《新课堂同步学习与探究》。这一章内容就基本没问题了，祝同学们顺利进入下一章的学习。

(我抽空打算录一个视频课，还没录过。但也要学，活到老学到老。)