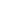[cf 947E] Perpetual Subtraction

题意

现在有个正整数\(x\)，你要进行\(m\)轮操作，每次将\(x\)随机变为\([0, x]\)中的一个整数。
问\(m\)轮之后，这个数为\(i(0 \leq i \leq x)\)的概率。

题解

考虑一个normaldp：设\(f_{i, j}\)表示第\(i\)轮后，这个数为\(j\)的概率，则：
\[ f_{i, j} = \sum_{k \geq j} f_{i - 1, k} * \frac{1}{k + 1} \]
则可以写出转移矩阵：
\[ T = \begin{bmatrix} 1 & \frac{1}{2} & \frac{1}{3} & \ldots & \frac{1}{n + 1} \\ 0 & \frac{1}{2} & \frac{1}{3} & \ldots & \frac{1}{n + 1} \\ 0 & 0 & \frac{1}{3} & \ldots & \frac{1}{n + 1} \\ \ldots & \ldots & \ldots & \ddots & \ldots \\ 0 & 0 & 0 & \ldots & \frac{1}{n + 1} \\ \end{bmatrix} \]
设初始向量为\(\vec b\)，则最后要求的是\(T ^ m \vec b\)。
这样是\(\mathcal O(n ^ 3 \log n)\)的。
考虑优化。像这样的线性递推，一般能做到\(\mathcal O(n ^ 2)\)，做到\(\mathcal O(n \log n \log k)\)的做法很难……

另辟蹊径。有一种高妙的相似对角化做法。
有定理，一个矩阵如果是线性无关的，则必定可以相似对角化。
设\(S = P T P ^ {-1}\)，其中\(P\)是可逆矩阵，\(S\)是对角矩阵。
求这个\(S\)的过程一般分为几步：求矩阵\(T\)特征值和特征向量->将特征向量当列向量排列于矩阵\(P\)中->计算\(S\)。

考虑\(T\)的特征值，特征值即满足\(\exists \vec v \neq \vec 0, T \vec v = \lambda \vec v\)的\(\lambda\)，其充要条件是\(|T - \lambda I| = 0\)。
由于
\[ |T - \lambda I| = \left | \begin{array} 1 - \lambda & \frac{1}{2} & \frac{1}{3} & \ldots & \frac{1}{n + 1} \\ 0 & \frac{1}{2} - \lambda & \frac{1}{3} & \ldots & \frac{1}{n + 1} \\ 0 & 0 & \frac{1}{3} - \lambda & \ldots & \frac{1}{n + 1} \\ \ldots & \ldots & \ldots & \ddots & \ldots \\ 0 & 0 & 0 & \ldots & \frac{1}{n + 1} - \lambda \\ \end{array} \right | = \left | \begin{array} 1 - \lambda & \lambda & 0 & \ldots & 0 \\ 0 & \frac{1}{2} - \lambda & \lambda & \ldots & 0 \\ 0 & 0 & \frac{1}{3} - \lambda & \ldots & 0 \\ \ldots & \ldots & \ldots & \ddots & \ldots \\ 0 & 0 & 0 & \ldots & \frac{1}{n + 1} - \lambda \\ \end{array} \right | = 0 \]
这个行列式直接用定义式求，得出
\[ (1 - \lambda)(\frac{1}{2} - \lambda)\ldots(\frac{1}{n + 1} - \lambda) = 0 \]
则所有特征值为\(1, \frac{1}{2}, \ldots, \frac{1}{n + 1}\)。

接着考虑特征向量，特征值即满足\(\exists \vec v \neq \vec 0, T \vec v = \lambda \vec v\)的\(\vec v\)。
尝试进行小范围的模拟计算，可以得出结果：
满足\(T \vec v_i = \frac{1}{i} \vec v_i\)的\(\vec v_i\)为
\[ \begin{bmatrix} (-1) ^ {i - 1} \binom{i - 1}{0} \\ (-1) ^ {i} \binom{i - 1}{1} \\ \ldots \\ (-1) ^ {i + i - 2} \binom{i - 1}{i - 1} \\ 0 \\ \ldots \\ 0 \\ \end{bmatrix} \]

---

proof1
则
\[ P = \begin{bmatrix} 1 & -1 & 1 & \ldots & (-1) ^ n \binom{n}{0} \\ 0 & 1 & -2 & \ldots & (-1) ^ {n + 1} \binom{n}{1} \\ 0 & 0 & 1 & \ldots & (-1) ^ {n + 2} \binom{n}{2} \\ \ldots & \ldots & \ldots & \ddots & \ldots \\ 0 & 0 & 0 & \ldots & (-1) ^ {n + n} \binom{n}{n} \\ \end{bmatrix} \]
而
\[ P ^ {-1} = \begin{bmatrix} 1 & 1 & 1 & \ldots & \binom{n}{0} \\ 0 & 1 & 2 & \ldots & \binom{n}{1} \\ 0 & 0 & 1 & \ldots & \binom{n}{2} \\ \ldots & \ldots & \ldots & \ddots & \ldots \\ 0 & 0 & 0 & \ldots & \binom{n}{n} \\ \end{bmatrix} \]
proof2
又因为\(S = P T P ^ {-1}\)即\(T = P ^ {-1} S P\)。有了\(P\)，\(S\)能用几次多项式卷积快速计算出。
但是如果\(S\)没有好的性质，也是无济于事的。但是事实证明，\(S\)是一个对角矩阵。
proof3
则
\[ \begin{aligned} ans & = T ^ m \vec b \\ & = (P ^ {-1} S P) ^ m \vec b \\ & = P ^ {-1} S (P P ^ {-1} S) ^ {m - 1} P \vec b \\ & = P ^ {-1} S ^ m P \vec b \\ \end{aligned} \]
考虑对角矩阵的幂次很好求，相当于把\(\vec b\)和前面几个矩阵依次用卷积卷一卷就出来了。
复杂度是\(\mathcal O(n \log m + n \log n)\)的。

proof1:
即证明\(T \vec v_i = \lambda_i \vec v_i\)，亦即\(\sum_{j} T_{k, j} \vec v_{i, j} = \lambda_i \vec v_{i, k}\)。
如下：
\[ \begin{aligned} \sum_{j} T_{k, j} \vec v_{i, j} & = \sum_{j = k} ^ n \frac{1}{j + 1} (-1) ^ {i + j} \binom{i}{j} \\ & = \sum_{j = k} ^ n \frac{1}{j + 1} (-1) ^ {i + j} \frac{i!}{j!(i - j)!} \\ & = \frac{1}{i + 1} \sum_{j = k} ^ n (-1) ^ {i + j} \frac{(i + 1)!}{(j + 1)!(i - j)!} \\ & = \frac{1}{i + 1} \sum_{j = k} ^ n (-1) ^ {i + j} \binom{i + 1}{j + 1} \\ & = \frac{1}{i + 1} \sum_{j = k} ^ n (-1) ^ {i + 1} \binom{j - i - 1}{j + 1} \\ & = \frac{(-1) ^ {i + 1}}{i + 1} \sum_{j = k} ^ n \binom{j - i - 1}{j + 1} \\ & = \frac{(-1) ^ {i + 1}}{i + 1} [\binom{i - i - 1 + 1}{i + 1} - \binom{k - i - 1}{k}] \\ & = \frac{(-1) ^ i}{i + 1} \binom{k - i - 1}{k} \\ & = (-1) ^ {i + k} \binom{i}{k} \\ & = \lambda_i v_{i, k} \\ \end{aligned} \]
其中用到了杨辉三角一斜列求和和牛顿二项式定理的导出式。
杨辉三角一斜列求和：
\[ \sum_{i = l} ^ r \binom {n + i}{m + i} = \binom{n + r + 1}{m + r} - \binom{n + l}{m + l - 1} \]
牛顿二项式定理的导出式：
\[ \binom{-n}{m} = (-1) ^ m \binom{n + m - 1}{m} \]

proof2:
即证明：
\[ \sum_{k = 1} ^ n {P ^ {-1}}_{i, k} P_{k, j} = [i = j] \]
又因为
\[ {P ^ {-1}}_{i, j} = \binom {j}{i} = \sum_{k = 0} ^ n [k = i] \binom{j}{k} \]
通过二项式反演，得
\[ [j = i] = \sum_{k = 0} ^ n (-1) ^ {j - k} {P ^ {-1}}_{i, k} \binom{j}{k} \]
则
\[ \begin{aligned} \sum_{k = 1} ^ n {P ^ {-1}}_{i, k} P_{k, j} & = \sum_{k = 1} ^ n (-1) ^ {j + k} \binom{j}{k} {P ^ {-1}}_{i, k} \\ & = \sum_{k = 0} ^ n (-1) ^ {j - k} \binom{j}{k} {P ^ {-1}}_{i, k} \\ & = [i = j] \end{aligned} \]

proof3:
由于
\[ \begin{aligned} T P & = T {[\vec v_1, \vec v_2, \vec v_3, \ldots, \vec v_{n + 1}]} ^ T \\ & = {[T \vec v_1, T \vec v_2, T \vec v_3, \ldots, T \vec v_{n + 1}]} ^ T \\ & = {[\lambda_1 \vec v_1, \lambda_2 \vec v_2, \lambda_3 \vec v_3, \ldots, \lambda_{n + 1} \vec v_{n + 1}]} ^ T \\ & = P \text{diag}(\lambda_1, \lambda_2, \lambda_3, \ldots, \lambda_{n + 1}) \\ \end{aligned} \]
则
\[ P ^ {-1} T P = \text{diag}(\lambda_1, \lambda_2, \lambda_3, \ldots, \lambda_{n + 1}) \\ \]
即\(S = P ^ {-1} T P\)是对角阵\(\text{diag}(\lambda_1, \lambda_2, \lambda_3, \ldots, \lambda_{n + 1})\)。

---

另附生成函数做法（图片出自_rqy's Blog）。

转载于:https://www.cnblogs.com/psimonw/p/11552565.html