机器学习基石(林轩田)学习笔记:Lecture 14 & Lecture 15

Lecture 14:Regularization

Regularized Hypothesis Set

当训练样本数不够多，而假设函数次数比较高时，很容易发生过拟合，正则化的目的就是希望让高维的假设函数退化成低维的假设函数

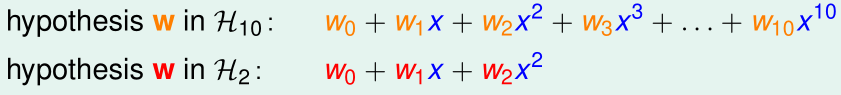
如上图，高维假设函数的参数里，高阶项对应的参数(w3,...,w10)就都被限制为0了

如果我们希望把\(\mathcal H_{10}\)退化为\(\mathcal H_{2}\)，加正则化的优化目标变成了：

\[\arg \min_{w\in \mathbb R^{10+1}} E_{in}(w)\]

\[\mathrm{s.t.}\ \ w_3=\cdots=w_{10}=0\]

这样做看起来是多此一举，直接用\(\mathcal H_2\)不就好了？实际上这是为后面的工作作铺垫。

现在我们要对这个优化目标的约束条件放宽一点：

\[\arg \min_{w\in \mathbb R^{10+1}} E_{in}(w)\]

\[\mathrm{s.t.}\ \ \sum_{i=0}^{10}1\{w_i\neq 0\}\leq 3\]

(约束条件放宽为，11个参数项里最多有3个不为0)

这个优化目标比之前的约束条件更宽松，但比没加约束的优化目标，发生过拟合的概率更低。

然而，求解这个优化目标是NP-Hard的，我们需要进一步将它的约束条件变成"软"约束：

\[\arg \min_{w\in \mathbb R^{10+1}} E_{in}(w)\ \ \mathrm{s.t.}\ \ \sum_{i=0}^{10} w_i^2\leq C\]

(注意，这个优化目标与上一个优化目标不是完全等价的)

约束条件可以看作是\(w^Tw\leq C\)，C就是向量W的最大长度，约束边界可以看作是一个超球面，C越大，表明对参数的限制越宽松。

Weight Decay Regularization

我们用矩阵形式重写上面的优化目标：

\[\arg \min_{w\in \mathbb R^{Q+1}} E_{in}(w)=\frac 1 n (Zw-y)^T(Zw-y)\]

\[\mathrm{s.t.}\ \ w^Tw\leq C\]

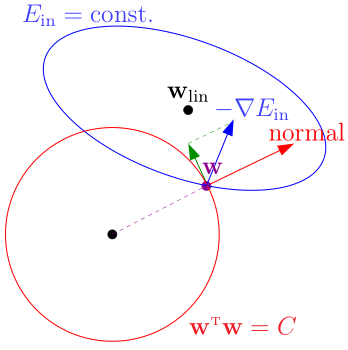
优化过程中，\(w\)沿\(-\nabla_w E_{in}\)的方向不断走，直到到达约束边界\(w^Tw=C\)

此时仍有优化的余地，为了不违反约束条件，我们把\(-\nabla_w E_{in}\)分解为两个分量：

• 红色向量(边界的法线方向)
• 绿色向量(边界的切线方向)

此时，我们保留绿色的分量，让w沿着绿色分量的方向走，直到绿色分量为0(即\(-\nabla_w E_{in}\)与红色向量平行)，表明到达了在约束条件下的最优点

有了几何上的直观理解后，我们就知道了，在这个约束条件下，最优点\(w_{REG}\)的条件是\(-\nabla_w E_{in}(w_{REG})\)与红色向量(方向为\(w_{REG}\))平行：

\[\nabla_w E_{in}(w_{REG})=kw_{REG}\]

改写为：

\[\nabla_w E_{in}(w_{REG})+\frac{2\lambda} n w_{REG}=0\]

\(\lambda\)被称为拉格朗日乘子

现在，我们的任务是求出\(w_{REG}\)

\[E_{in}(w)=\frac 1 n (Zw-y)^T(Zw-y)\]

\[\nabla_w E_{in}=\frac 2 n (Z^TZw-Z^Ty)\]

\[\frac 2 n (Z^TZw_{REG}-Z^Ty)+\frac {2\lambda} n w_{REG}=0\]

\[w_{REG}=(Z^TZ+\lambda I)^{-1}Z^Ty\]

其中，\(Z^TZ\)是半正定的，如果\(\lambda >0\)，则\(\lambda I\)是正定的，\(Z^TZ+\lambda I\)也就是正定的，进一步可以推出\(Z^TZ+\lambda I\)一定可逆

上述的线性回归被称为Ridge Regression(岭回归)

下面，我们把正则化推广到更一般的情况：在逻辑回归等问题中，\(w_{in}\)不能得到解析解，但可以求出数值解，在这种情况下，下面介绍求出\(w_{REG}\)的数值解的方法

\(\nabla_w E_{in}(w_{REG})\)是\(E_{in}(w)\)对w的导数，\(\frac{2\lambda} n w_{REG}\)是\(\frac{\lambda} n w^Tw\)对w的导数

所以满足\(\nabla_w E_{in}(w_{REG})+\frac{2\lambda} n w_{REG}=0\)的点\(w_{REG}\)可以使\(E_{in}(w)+\frac \lambda n w^Tw\)取得极小值

于是问题可以看作是最小化\(E_{aug}(w)=E_{in}(w)+\frac \lambda n w^Tw\)，其中第二项就是正则化项(regularizer)，我们称\(E_{aug}(w)\)为增广误差(augmented error)

我们可以用梯度下降、牛顿法等方法最优化这个\(E_{aug}(w)\)来得到\(w_{REG}\)的数值解

假如目前输入特征只有\(x\in[-1,1]\)，通过特征变换映射到Q阶，Q很大时，高阶的\(x^q\)会变得很小，为了产生和低阶的\(w_ix^i\)一样的影响力，此时\(x^q\)前的参数就要用更大的\(w_q\)

为了解决这个问题，我们可以改变特征变换函数，采用勒让德多项式

Regularization and VC Theory

下面我们把正则化与VC理论联系起来，首先回顾增广误差与VC Bound:

在增广误差中，正则化项的\(w^Tw\)是与假设函数的复杂度正相关的

而VC Bound里的\(\Omega (\mathcal H)\)也是与假设函数的复杂度正相关的。

在没有正则化时，我们用\(E_{in}\)来近似估计\(E_{out}\)，在加了正则化后，如果\(\frac \lambda n w^Tw\)与\(\Omega (\mathcal H)\)很相似的话，\(E_{aug}\)对\(E_{out}\)的近似程度将明显比\(E_{in}\)对\(E_{out}\)的近似程度高。

在加入正则化后，假设函数集\(\mathcal H\)被缩小到一个更小的子集\(\mathcal H(C)\subset \mathcal H\)中(其中每个假设函数都满足约束条件)，而类似Lecture 12的证明，我们也可以证明出\(d_{VC}(\mathcal H(C))\leq d_{VC}(\mathcal H)\)，所以正则化起到了减小VC维的作用。

General Regularizers

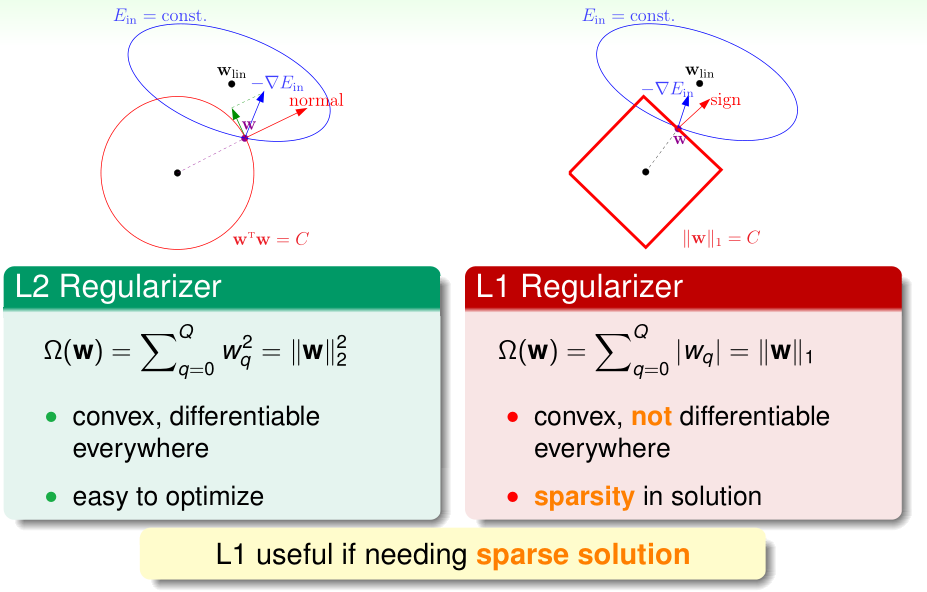
之前我们介绍的正则化项被称为L2正则化(因为其约束条件对应于\(\|w\|_2^2\leq C\))，L2正则化非常常用

这里介绍的L1正则化，约束条件对应于\(\|w\|_1\leq C\)，一般使用L1正则化是为了得到更稀疏的参数w(w中很多项都是0，这样实际的参数数量少很多，从而可以加速预测过程)

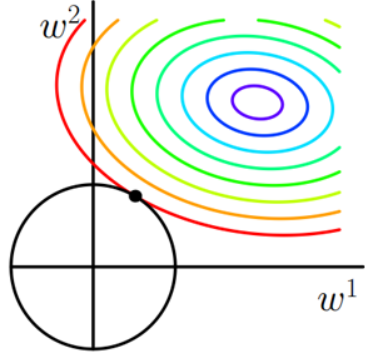
为什么L1正则化可以得到更加稀疏的参数向量w呢？首先我们回顾一下，在有约束条件时最优的\(w_{REG}\)，\(\nabla_wE_{in}(w_{REG})\)方向应该与约束边界法向量平行，换言之，就是\(E_{in}\)的等高线与约束边界相切于\(w_{REG}\)，如上图所示

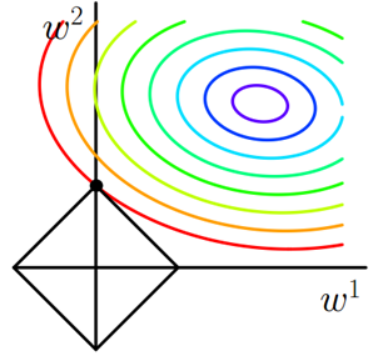
L1正则化相当于是要求\(\|w\|_1\leq C\)，当参数数量为2时，在坐标系里看就是一个正菱形，我们再把\(E_{in}\)的等高线图画在坐标系里，可见等高线相切于菱形的顶点的概率更高，对应的w中的0也就更多了，这就解释了为何L1正则化可以得到更加稀疏的参数向量w

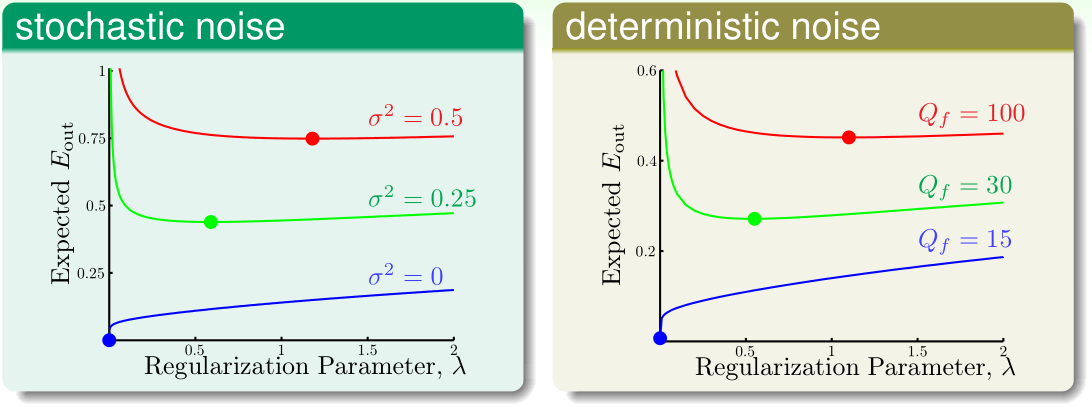
在有随机噪声\(\sigma^2\)和确定噪声\(Q_f\)的两种情况下，随着噪声强度不断变大，\(E_{out}\)最小的\(\lambda\)也随之变大

Lecture 15:Validation

Model Selection Problem

在机器学习中，我们经常遇到模型选择问题。例如在二分类问题中：

• 1、选择最佳的学习算法：PLA/口袋算法/线性回归实现二分类/逻辑回归
• 2、梯度下降算法中的学习率的选择
• 3、特征变换函数\(\Phi\)的选择
• 4、正则化项的选取
• 5、正则化参数\(\lambda\)的选取

我们可以把模型选择问题抽象为：

现在给定训练集\(\mathcal D\)，有M个假设函数集\(\mathcal H_1,\cdots,\mathcal H_M\),它们对应M个学习算法\(\mathcal A_1,\cdots,\mathcal A_M\)

这些学习算法分别选出了每个集合\(E_{in}(E_{aug})\)最小的假设函数\(g_i=\mathcal A_i(\mathcal D)\)

我们要从M个\(g_i\)里选一个最优的\(g_{m^*}\)，使得\(E_{out}(g_{m^*})\)尽可能小

显然，我们不能再拿训练集\(\mathcal D\)去计算每个\(E_{in}(g_i)\)来近似估计\(E_{out}(g_i)\)，因为往往过拟合的\(g_i\)的\(E_{in}\)更小

Validation

交叉验证就是把大小为n的原始训练集\(\mathcal D\)拆成：大小为n-k的训练集\(\mathcal D_{train}\)，和，大小为k的验证集\(\mathcal D_{val}\)

我们用假设函数h在验证集上的误差\(E_{val}(h)\)来近似估计\(E_{out}(h)\)

令\(\mathcal H=\{g_1^-,\cdots,g_M^-\}\)

其中\(g_1^-=\mathcal A_1(\mathcal D_{train}),\cdots,g_M^-=\mathcal A_M(\mathcal D_{train})\)

然后，我们选其中\(E_{val}(g_i^-)\)最小的i作为\(m^*\)

\[m^*=\arg \min_{i} E_{val}(g_i^-)\]

\[g_m^-=\mathcal A_{m^*}(\mathcal D_{train})\]

根据Lecture 4 \(\mathcal H\)为有限集时的不等式，有：

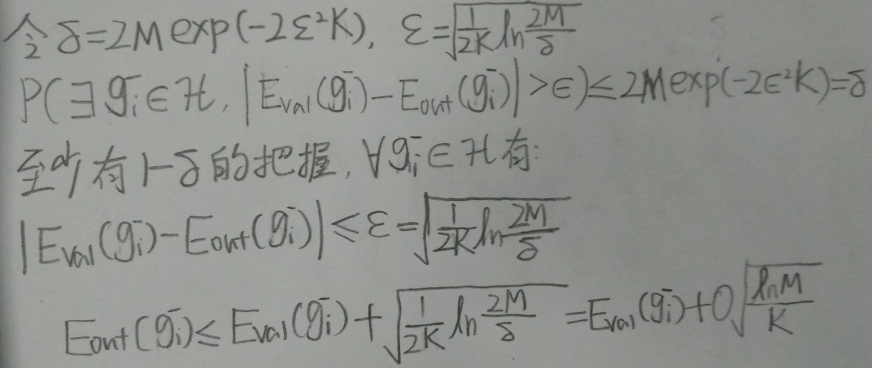
该不等式对\(g_m^-\in \mathcal H\)同样成立：

由于\(M=|\mathcal H|\)很小，所以\(E_{out}(g_m^-),E_{val}(g_m^-)\)非常接近，而且验证集样本数K越大，二者接近的程度也就越大。

最后，我们用整个原始训练集\(\mathcal D\)对\(\mathcal A_{m^*}\)重新训练一次，得到最终的\(g_{m^*}=\mathcal A_{m^*}(\mathcal D)\)

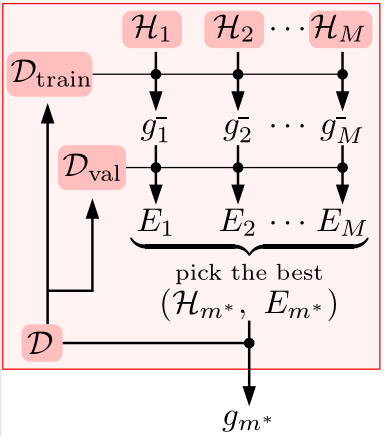
整个模型选择的流程如上图所示

在K很小时，训练样本损失不多，我们有\(E_{out}(g)\approx E_{out}(g^-)\)

在K很大时，根据刚刚推出的结论，我们有\(E_{out}(g^-)\approx E_{val}(g^-)\)

一般而言，验证集大小K选取为N/5比较合适

Leave-One-Out Cross Validation

Leave-One-Out Cross Validation在CS229中已经提及，这里不赘述它的具体实现

令\(e_i=\)用第i个训练样本当验证数据，其他n-1个样本训练出的\(g_i^-=\mathcal A(\mathcal D-(x^{(i)},y^{(i)}))\)，在验证数据\((x^{(i)},y^{(i)})\)上得到的误差\(err(g_i^-(x^{(i)}),y^{(i)})\)

则通过Leave-One-Out Cross Validation得到的验证误差

表明Leave-One-Out Cross Validation得到的验证误差是可以近似估计\(E_{out}(\mathcal A(\mathcal D))\)的

V-Fold Class Validation

V-Fold Class Validation是Leave-One-Out Cross Validation和原始的交叉验证方法的折中，它将训练集拆成互不相交的、大小相同的V份，每次只用其中V-1份训练，用剩下那一份交叉验证，获得\(E_{val}^{(i)}(g_i^-)\)，最终得到的验证误差为

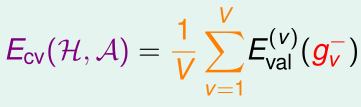
V-Fold Class Validation在CS229中也提过，这里不再赘述

转载于:https://www.cnblogs.com/qpswwww/p/9366442.html