k均值聚类算法考试例题_K-means 聚类算法

1. K-means 聚类算法的基本原理

Kmeans是无监督学习的代表，没有所谓的Y。主要目的是分类，分类的依据就是样本之间的距离。比如要分为K类。步骤是：

1. 随机选取K个点。
2. 计算每个点到K个质心的距离，分成K个簇。
3. 计算K个簇样本的平均值作新的质心
4. 循环2、3
5. 位置不变，距离完成

2. 关于聚类的距离

Kmeans的基本原理是计算距离。一般有三种距离可选：

曼哈度距离：

曼哈度距离

欧式距离：

欧式距离

余弦距离：

余弦距离

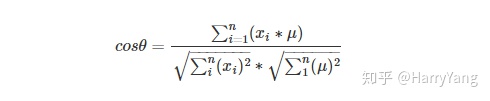
3. Inertia的概念

每个簇内到其质心的距离相加，叫inertia。各个簇的inertia相加的和越小，即簇内越相似。（但是k越大inertia越小，追求k越大对应用无益处）

4. 在sklearn中用实现代码

导入模拟数据，并绘图查看其分布

#导入数据
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
X, y = make_blobs(n_samples=500, # 500个样本
                 n_features=2, # 每个样本2个特征
                 centers=4, # 4个中心
                 random_state=1 #控制随机性
                 )
#画出对应的图像位置
color = ['red', 'pink','orange','gray']
fig, axi1=plt.subplots(1)
for i in range(4):
    axi1.scatter(X[y==i, 0], X[y==i,1],
               marker='o',
               s=8,
               c=color[i]
               )
plt.show()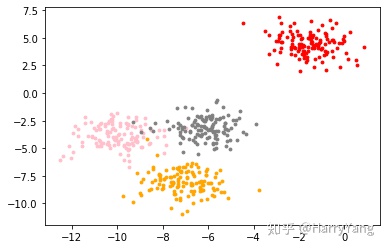

使用Sklearn中的K-means进行建模：

from sklearn.cluster import KMeans
n_clusters=4  #划分类别的数量
cluster = KMeans(n_clusters=n_clusters,random_state=0).fit(X)

利用训练的模型进行预测：

y_pred=cluster.predict(X)
y_pred.shape#数字比较多，只查看其形状
(500,)

查看质心及Inertia

centroid=cluster.cluster_centers_
centroid # 查看质心
array([[ -6.08459039,  -3.17305983],
       [ -1.54234022,   4.43517599],
       [ -7.09306648,  -8.10994454],
       [-10.00969056,  -3.84944007]])
inertia=cluster.inertia_
inertia
908.3855684760613

5. 通过绘图查看分类后的分布

color=['red','pink','orange','gray']
fig, axi1=plt.subplots(1)
for i in range(n_clusters):
    axi1.scatter(X[y_pred==i, 0], X[y_pred==i, 1],
               marker='o',
               s=8,
               c=color[i])
axi1.scatter(centroid[:,0],centroid[:,1],marker='x',s=100,c='black')
<matplotlib.collections.PathCollection at 0x8a50510>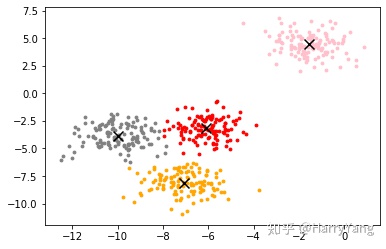

6. 总结

以上是本周对KMeans聚类算法的原来的初步讲解，并对通过代码来实现。