DTW算法Python实现

DTW算法可以用来衡量两个时间序列的相似性，而且两个时间序列的长度可以不必相等。

DTW算法原理

如图1所示，图中矩阵$dij$表示时间序列$A$时刻$i$和时间序列$B$时刻$j$的距离，DTW算法就是要从$(1,1)$到$(m,n)$找到一条路径使得累计$dij$最小。

图1：DTW算法示意图，r表示warping window，红色圆点表示累计距离最小的路径。

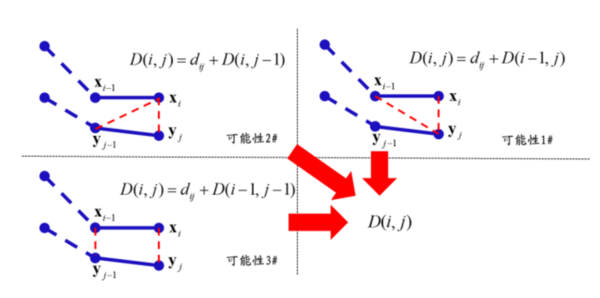
如何找到这条路径呢，我们这里采用动态规划算法。假设我们要求到位置$(i,j)$的最小累计距离$D(i,j)$，那么它只能由$D(i-1,j)$，$D(i,j-1)$和$D(i,j)$这三个位置的最小累计距离中寻找，也就是$D(i,j)=dij+min[D(i-1,j),D(i,j-1),D(i,j)]$。如图2所示，最优路径只能从三个临近位置寻找。最终，$D(m,n)$越小，表示两个时间序列间的相似性越高。