学习小记-----行列式&&矩阵树定理Kirchhoff's theorem

为什么我的标题要加上Kirchhoff's theorem呢,是因为之前我查这个定理是用这个英文在谷歌上查的,然后,,,,我看了20多分钟的英文维基百科,然后爬墙去做别的题目了QAQ

---

 

行列式

 

前置知识

基础的线性代数的知识

基本的数学知识

定义

 

名词规定(其实就是一些可以一句话带过的前置知识)(雾)

• 排列－＞就是把数字集合有序放置，如果是N阶排列就是这个数字集合内数字为１～ｎ
• 逆序(对)－＞设一个数A位置为LL,另一个数B位置为GG,如果LL>GG但是A<B则称其为逆序
• 奇OR偶排列－＞如果一个排列中逆序数目为奇数,就是奇排列,反之即为偶排列
  • 对换－＞把一个序列中任意两个数对换位置，其余数不变，则称其为一个对换
    • 一个定理，一次对换会改变序列的奇偶性
    • 证明：如果你调换的是一个逆序，则代表你消灭了一个逆序，所以逆序数目减一，由奇偶计算可知，逆序数目会变为相反的奇偶，同理，如果你调换的不是一个逆序，那么你增加了逆序数目＊１，所以逆序奇偶性发生变换．所以此定理成立

行列式定义为什么明明也是名词定义的内容我要单独拿出来呢,,,,因为我乐意略略路

• 对于一个矩阵，它的行列式是——
  

  

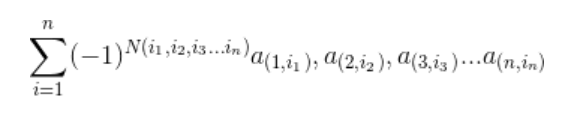
• N(i1,i2,i2..in)表示这个序列的逆序数目

• (i1,i2,...in)是一个1到n的排列

• 而一个n*n的矩阵行列式可以被记为det(A)，或者是|A|

• 用高斯消元实现

性质

• 行列互换，行列式不变

  • 就是把所有的ａ_i,j换为a_j,i  但是在N(XXX)中,每一个依旧都会再出现一次,最后的结果还是一样的
    
• 两行交换,行列式取反
  • 由对换的定理,我们可知,对换会改变排列的奇偶性,所以(-1)的指数奇偶性会变,所以行列式取反
• 行列式中,因子可以提出,行列式不发生改变
  • 首先是逆序，逆序只在意相对大小，所以不变化．其次是排列，就是把求和公式里提取一个公因数而已
    • 由对排列不变的证明（？）可知，如果某一行 *=k OR /=k，他也是不变的
• 某两行相同，则行列式为０
  • 如果交换两行，行列式变号，可矩阵没有任何变化，所以行列式又应该不变。所以行列式为 0
  • 同理可知,若两列成倍数关系,则行列式也是0
    
    • 其实就是提出一个公因子后,就变为了两行相同了
• 某行加上了另一行的K倍,行列式也不会发生改变
  • 若ｉ行每一个数都增加了ｋ＊A_ｊ，则由∑的性质，我们可以把第ｉ行的求和公式拆为ｉ的求和加上ｋ＊Ａ_ｊ的求和公式，此时，后者和第ｊ行成倍数关系，所以求出的行列式为０，对最后答案没影响，所以成立
• 一个矩阵行列式等于上三角矩阵的主对角线的乘积
  • 不清楚，不了解，不会证，背过它，我叫不知道

求解

利用高斯消元求解，由于精度问题，行列式不可出现小数（提问，小数是奇数还是偶数）所以要用辗转相除法的高斯消元来求，时间复杂度是O(N^3logN)

 

 1 inline int gauss(int n){
 2         //利用辗转相除术进行高斯消元
 3         //之所以用辗转相除，只为了保持精度
 4         int ans=1;
 5         for(register int i=1;i<=n;i++){
 6             for(register int k=i+1;k<=n;k++){
 7                 while(a[k][i]){
 8                     int d=a[i][i]/a[k][i];
 9                     for(register int j=i;j<=n;j++) 
10                         a[i][j]=(a[i][j]-1LL*d*a[k][j]%mod+mod)%mod;
11                     swap(a[i],a[k]),ans=-ans;
12                     //交换行，行列式改变
13                 }
14             }
15             ans=1ll*ans*a[i][i]%mod,ans=(ans+mod)%mod;
16             //求解行列式
17         }
18         return ans;
19     }

 

---

矩阵树定理----Kirchhoff's theorem

定义

(翻译自维基百科并加上我的一些理解QAQ好怕出锅)

在数学的图论领域中,基尔霍夫定理或基尔霍夫矩阵树定理，是由古斯塔夫·基尔霍夫所命名的一个算法.其算法是关于求解一个图中的生成树的数目.这个算法可以在计算器中,以拉普拉斯矩阵为基准,在以多项式时间内求解．同时，他作为Ｃayley公式的推广，它可以在完全图中求解出生成树的数目．

基尔霍夫定理以拉普拉斯矩阵的定义为基础．拉普拉斯矩阵等于原图的度数矩阵(以矩阵的形式记录每个点的出入度之和)减去邻接矩阵(以矩阵的方式记录点于点之间是否连边,连边为1,否则为0)之差．

对于给定的有N的点的连通图G，我们用λ₁, λ₂, ..., λ_n−1来标记在拉普拉斯矩阵中特质值不为０(就是数值不为０）的点，生成树的数目就是

举个例子

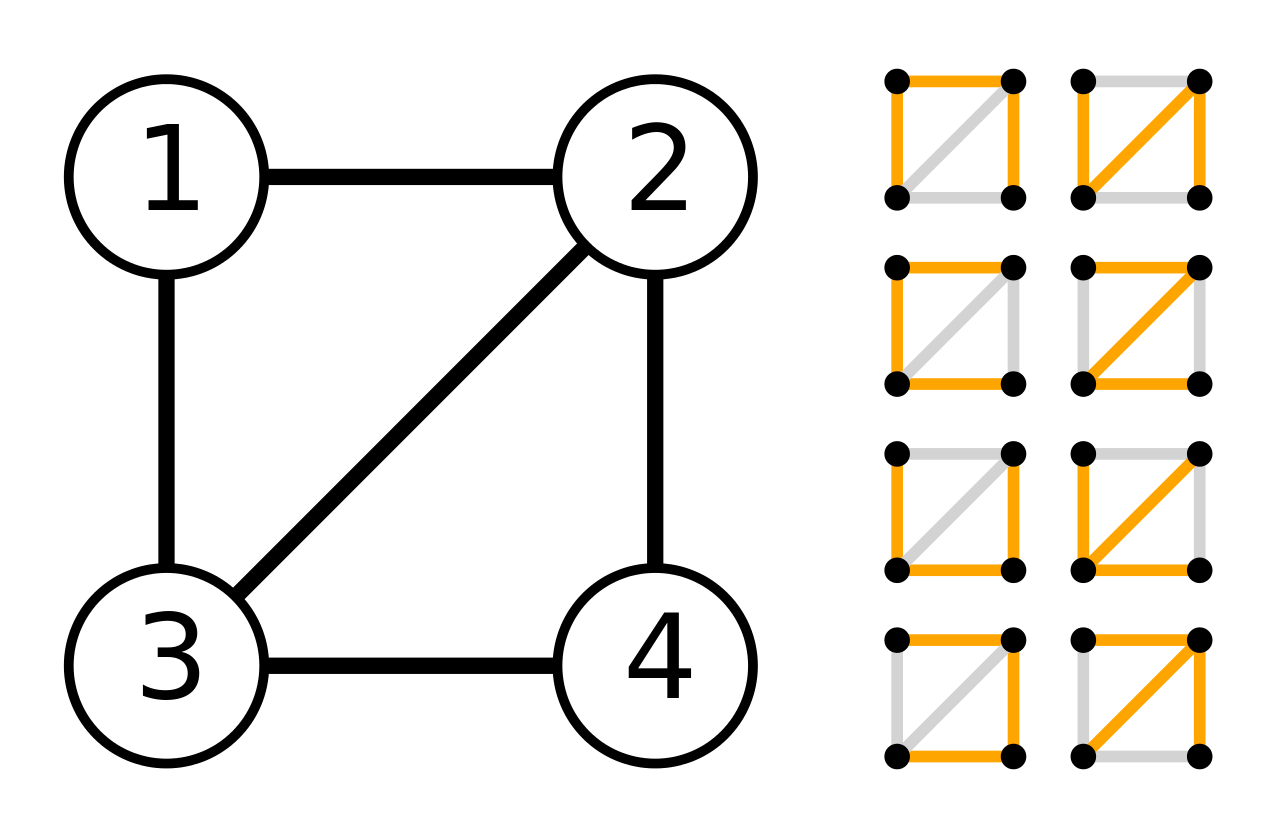
在上图中,菱形图G的拉普拉斯矩阵Q为

 

接下来，构造一个矩阵Q^＊，构造方式就是在原矩阵Q中删去任意第ｒ行和第ｒ列，以删去第一行第一列为例

 

 

最后Q^＊的行列式可求得为８，故，原图的生成树数目也为８

NOTICE(译者加)：此算法适用于无向图中，允许重边和自环在维基百科下面还有证明，但是由于译者（懒）水平有限，故而无法翻译或者自己给出证明方式，感兴趣的同学可以去看看这篇博客给出的证明．

NOTICE(译者加)：关于邻接矩阵与度数矩阵

• 邻接矩阵就是若原图中两点（x,y）有边，则 G(x,y)++,G(y,x)++;
• 度数矩阵就是若原图中点x与y有边,则D(x,x)++,D(y,y)++;
• 所以可以简化为a[x][y]--,a[y][x]--,a[x][x]++,a[y][y]++;

求解

 1 inline void add(int x,int y){
 2         --a[x][y],--a[y][x],++a[x][x],++a[y][y];
 3         //构造基尔霍夫矩阵
 4     }
 5 
 6 inline int gauss(int n){
 7         //利用辗转相除术进行高斯消元
 8         //之所以用辗转相除，只为了保持精度
 9         int ans=1;
10         for(register int i=1;i<=n;i++){
11             for(register int k=i+1;k<=n;k++){
12                 while(a[k][i]){
13                     int d=a[i][i]/a[k][i];
14                     for(register int j=i;j<=n;j++) 
15                         a[i][j]=(a[i][j]-1LL*d*a[k][j]%mod+mod)%mod;
16                     swap(a[i],a[k]),ans=-ans;
17                     //交换行，行列式改变
18                 }
19             }
20             ans=1ll*ans*a[i][i]%mod,ans=(ans+mod)%mod;
21             //行列式求解
22         }
23         return ans;
24     }
25 
26 int ans=1;
27 ans=1ll*ans*gauss(n-1)%mod;
28 //求解N*N大小的矩阵的生成树数目

---

后记

注册博客园账号更多的是心血来潮，但是还是感谢可能存在的因为我的博客而受益的人愿意看，以及某P姓大佬的,,,,,菲克．可能是因为这篇博客耗费我时间最长了（不算查资料和准备时间，我从早上九点写到十二点），所以可能才会有这篇后记吧．也算是一个难忘的回忆了．希望我AFO几年后，等到我心态更成熟一些时,看着我写过的东西，笑着说，这就是我曾经的青春啊，玫金色的爱恋伴以蔚蓝色的忧伤，白银色的笔尖辅以浅紫色的键盘，机房中回荡的笑声加上哭泣的眼泪，如同初春的青梅，苦涩与甜蜜交织，画出我记忆中最美好的时光

NOTICE：本博客代码参考自Siyuan,如有侵权,立马修改

转载于:https://www.cnblogs.com/fallen-down/p/11206442.html