欧几里得旅行商问题 java与c++实现

最新推荐文章于 2021-02-16 20:26:58 发布

weixin_30756499

最新推荐文章于 2021-02-16 20:26:58 发布

阅读量108

点赞数

文章标签： java c/c++ 数据结构与算法

原文链接：http://www.cnblogs.com/wennian/p/5036925.html

版权

双调欧几里得旅行商问题是一个经典动态规划问题。《算法导论（第二版）》思考题15-1

旅行商问题描述：平面上n个点，确定一条连接各点的最短闭合旅程。这个解的一般形式为NP的（在多项式时间内可以求出）

J.L. Bentley 建议通过只考虑双调旅程(bitonictour)来简化问题,这种旅程即为从最左点开始，严格地从左到右直至最右点，然后严格地从右到左直至出发点。下图(b)显示了同样的7个点的最短双调路线。在这种情况下，多项式的算法是可能的。事实上，存在确定的最优双调路线的O(n*n)时间的算法。

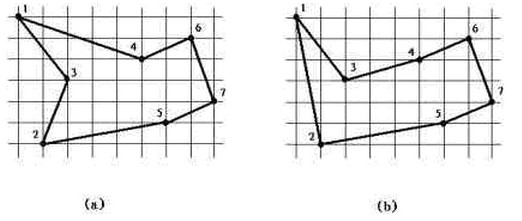
上图中，a是最短闭合路线，这个路线不是双调的。b是最短双调闭合路线

以上截取来自：http://blog.csdn.net/xiajun07061225/article/details/8092247

/**
 * 欧几里得旅行商(travelling salesman problem)问题
 *   分解模型：
 *        一个人从Pi严格递减的走到P1，然后再严格递增的回到Pj，求总路径的最小值,其中P1,P2,...,Pj的
 *        所有节点都要走一次，求最短的路径；
 *        对于1 <= i <= j <= n, 我们定义P(i, j)是一条包含了P1, P2, P3 ...Pj的途径
 *        这条路径可以分成2部分：递减序列与递增序列：起点是Pi(1 <= i <= j)，拐点是P1，
 *        终点是Pj, P[i, j]为其最小值；路径为（Pi-_>Pm-->P1-->Pn-->Pj，其中1<m<i<n<j） 
 *   动态规划方程：
 *   	  p[i,j]为最小值，dist(m,n)为m与n的直接距离
 *        p[1,2]=dist(1,2)
 *        i<j-1时，从P(i+1)到Pj之间的点必然出现在递增序列中
 *              p[i,j]=p[i,j-1]+dist(j-1,j)
 *        i=j-1时，假设P1到Pi之间的一个中间节点Pk，使得p[k,i]+dist(k,j)最小，也就是说，找到了
 *              将P1到Pj的所有节点走一遍的最短路径
 *              p[i,j]=min{p[k,i]+dist(k,j)}(其中1<=k<=i)
 *        p[k,i]又可以按照以上方式继续找出最小路径
 *        
 *        对于欧几里得旅行商问题，要求的最短路径是p[n,n]
 *        p[n,n]=p[n-1,n]+dist(n-1,n);
 *       
 *   
 */

</pre><pre name="code" class="html">

以下是C++实现，来自：http://blog.csdn.net/xiajun07061225/article/details/8092247

#include <iostream>
#include <cmath>
#include <iomanip>

using namespace std;

const int n = 7;//点的数目
const int MaxVal = 999999;
const int MaxLen = 201;

struct tagPoint{
	double x,y;
};

//计算点i和点j之间的直线距离
double distance(tagPoint *points,int i,int j)
{
	return sqrt((points[i].x - points[j].x) * (points[i].x - points[j].x) +
		(points[i].y - points[j].y) * (points[i].y - points[j].y));
}

double DP(tagPoint *points,int n)
{
	double b[MaxLen][MaxLen];//记录最短路径的长度
	//计算所有情况下的b[i][j]，1 <= i <= j
	//初始化
	b[1][2] = distance(points,1,2);
	for (int j = 3;j <= n;++j)
	{
		//i < j-1
		for (int i = 1;i <= j - 2;++i)
		{
			b[i][j] = b[i][j - 1] + distance(points,j - 1,j);
		}
		//i = j - 1,b[i][j] = min(b[k][j - 1] + distance(k,j));
		b[j - 1][j] = MaxVal;
		for (int k = 1;k <= j - 2;++k)
		{
			double temp = b[k][j - 1] + distance(points,k,j);
			if (temp < b[j - 1][j])
			{
				b[j - 1][j] = temp;
			}
		}
	}

	b[n][n] = b[n - 1][n] + distance(points,n - 1,n);

	return b[n][n];
}

int main()
{
	int NUM;
	while(cin >> NUM)
	{
		tagPoint *points = new tagPoint[NUM + 1];
		for (int i = 1;i <= NUM;++i)
		{
			cin >> points[i].x;
			cin >> points[i].y;
		}
		double minDis = DP(points,NUM);
		//设置输出格式：精确到小数点后2位
		cout.setf(ios::fixed);
		cout << setprecision(2) << minDis << endl;
	}
}

以下是java实现，基本思想是一样的。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Scanner;

import org.omg.CORBA.PRIVATE_MEMBER;

/**
 * @date 2014-09-20
 * @author acer
 * 欧几里得旅行商(travelling salesman problem)问题
 *   分解模型：
 *        一个人从Pi严格递减的走到P1，然后再严格递增的回到Pj，求总路径的最小值,其中P1,P2,...,Pj的
 *        所有节点都要走一次，求最短的路径；
 *        对于1 <= i <= j <= n, 我们定义P(i, j)是一条包含了P1, P2, P3 ...Pj的途径
 *        这条路径可以分成2部分：递减序列与递增序列：起点是Pi(1 <= i <= j)，拐点是P1，
 *        终点是Pj, P[i, j]为其最小值；路径为（Pi-_>Pm-->P1-->Pn-->Pj，其中1<m<i<n<j） 
 *   动态规划方程：
 *   	  p[i,j]为最小值，dist(m,n)为m与n的直接距离
 *        p[1,2]=dist(1,2)
 *        i<j-1时，从P(i+1)到Pj之间的点必然出现在递增序列中
 *              p[i,j]=p[i,j-1]+dist(j-1,j)
 *        i=j-1时，假设P1到Pi之间的一个中间节点Pk，使得p[k,i]+dist(k,j)最小，也就是说，找到了
 *              将P1到Pj的所有节点走一遍的最短路径
 *              p[i,j]=min{p[k,i]+dist(k,j)}(其中1<=k<=i)
 *        p[k,i]又可以按照以上方式继续找出最小路径
 *        
 *        对于欧几里得旅行商问题，要求的最短路径是p[n,n]
 *        p[n,n]=p[n-1,n]+dist(n-1,n);
 *        解释：Pn-->Pn,如果第一个点是Pn-1，那么上面的式子显然成立；
 *        	      如果第一个点是Pk,（1<=k<=n-2），那么Pn-1一定在Pk-->Pn的递增序列中，所以
 *            p[n,n]=p[k,n]+dist(k,n)=p[k,n-1]+dist(n-1,n)+dist(k,n);
 *            其中p[n-1,n]=p[k,n-1]+dist(k,n)
 *            所以 p[n,n]=p[n-1,n]+dist(n-1,n)必然成立;
 *       
 *   
 */
public class TSProblem {

	
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		String  line=null;//读取每一行的输入数据
		int[][] pointXY;//记录横纵坐标
		
		System.out.print("请输入点的个数N：");
		InputStreamReader isr=new InputStreamReader(System.in);
		BufferedReader bReader=new BufferedReader(isr);
		try {
			line=bReader.readLine().toString();
		} catch (IOException e) {
			// TODO Auto-generated catch block
			e.printStackTrace();
		}
		int n=Integer.parseInt(line);//记录点的个数
		pointXY=new int[n][2];
		
		System.out.println("请输入每个点的坐标，坐标格式为:x,y  (以EOF结束输入)");
		Scanner scn=new Scanner(System.in);
		int i=0;
		while(!"EOF".equals(line=scn.nextLine())){
			String[] p=line.split(",");
			int j=0;
			for(String str:p){
				pointXY[i][j++]=Integer.parseInt(str);			
			}
			i++;
			if(i>=n){
				System.out.println("输入的点数已经足够，自动结束输入");
				break;//退出输入
			}
			
		}
		
		//System.out.println("ok");
		int length=pointXY.length;
		TSProblem tsp=new TSProblem(pointXY,length);
		
		
		

	}
	
	public TSProblem(int[][] points,int length){
		//points中存储所有的节点，乱序排列
		//1、首先将所有的节点按照x坐标顺序排列，可选用多种排序方式，这里采用快排，时间复杂度为o(nlogn)	
		points=this.QuickSort(points, 0, length-1);
//		//打印排序后的点
//		for(int i=0;i<length;i++){
//			System.out.println(points[i][0]+","+points[i][1]);
//		}
		
		//2、找到最短路径
		double leastDis=DP(points, length);
		
		System.out.println("最短路径为："+leastDis);
		
		
		
	}
	
	
	//计算最短旅行路径
	double DP(int[][] points,int length){
		
		//p用于记录最短路径的长度
		double[][] p=new double[length][length];
		p[0][1]=dist(points, 0, 1);
		for(int j=2;j<length;j++){
			//case1:i<j-1
			// p[i,j]=p[i,j-1]+dist(j-1,j)
			for(int i=0;i<j-1;i++){
				p[i][j]=p[i][j-1]+dist(points, i, j);
			}
			
			//case2:i=j-1
			// p[i,j]=min{p[k,i]+dist(k,j)}(其中1<=k<=i)
			p[j-1][j]=Float.MAX_VALUE;
			double temp=0;
			for(int k=0;k<j-1;k++){
				temp=p[k][j-1]+dist(points, k, j);
				if(temp<p[j-1][j]){
					p[j-1][j]=temp;
				}
			}
			
			
		}
		p[length-1][length-1]=p[length-2][length-1]+dist(points, length-2, length-1);
		
		//返回Pn-->Pn，即最短路径
		return p[length-1][length-1];
		
	}
	
	//计算两点之间的直接距离dist(i,j)
	double dist(int[][] point ,int i,int j){
		double distance=0;
		distance=Math.sqrt(Math.pow((point[j][0] -point[i][0]),2)
				           +Math.pow((point[j][1]-point[i][1]),2));
		
		return distance;		
	}
	
	//快排
	int[][] QuickSort(int[][] num,int left,int right){
		/**
		 * 1、先从数列中取出一个数作为基数
		 * 2、大数置于该数的右边，小数置于该数的左边
		 * 3、重复步骤1,2
		 */
		if(left<right){
			int tempX=num[left][0];//设置基数，不唯一
			int tempY=num[left][1];
			int i=left,j=right;
			while(i<j){
				while(i<j&&num[j][0]>=tempX)
					j--;	//右边的数小于基数时退出
				if(i<j){
					//如果在右边找到一个数小于基数，num[i]此时为空，将该数填到num[i]
					num[i][0]=num[j][0];
					num[i][1]=num[j][1];
					i++;
				}
				while(i<j&&num[i][0]<tempX)
					i++;	//左边的数大于基数时退出
				if(i<j){
					//如果在左边找到一个数大于基数，num[j]此时为空，将该数填到num[j]
					num[j][0]=num[i][0];
					num[j][1]=num[j][1];
					j--;
				}
							
			}//当i=j时退出
			//num[i]为空值，将基数填入
			num[i][0]=tempX;
			num[i][1]=tempY;
			
			QuickSort(num, left, i-1);//左边快排
			QuickSort(num, i+1, right);//右边快排		
			
		}
		//返回已经排好序的数组
		return num;	
	}
	
}

转载于:https://www.cnblogs.com/wennian/p/5036925.html

weixin_30756499

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
欧几里得旅行商问题 java与c++实现

双调欧几里得旅行商问题是一个经典动态规划问题。《算法导论（第二版）》思考题15-1旅行商问题描述：平面上n个点，确定一条连接各点的最短闭合旅程。这个解的一般形式为NP的（在多项式时间内可以求出）J.L. Bentley 建议通过只考虑双调旅程(bitonictour)来简化问题,这种旅程即为从最左点开始，严格地从左到右直至最右点，然后严格地从右到左直至出发点。下图(b)...
复制链接

扫一扫