C++ MD5哈希算法实现详解

本文还有配套的精品资源，点击获取

简介：MD5是一种广泛使用的哈希函数，用于将任意长度的数据转换为固定长度的128位摘要。本文提供了在C++中实现MD5算法的详细步骤，包括数据预处理、初始化状态、执行迭代过程和组合结果。同时，介绍了如何使用openssl库简化实现过程，以及在DEV环境下编译和运行MD5代码时应注意的内存管理、错误处理、编码兼容性和代码组织问题。MD5的实现是理解哈希算法和提高编程技能的重要实践。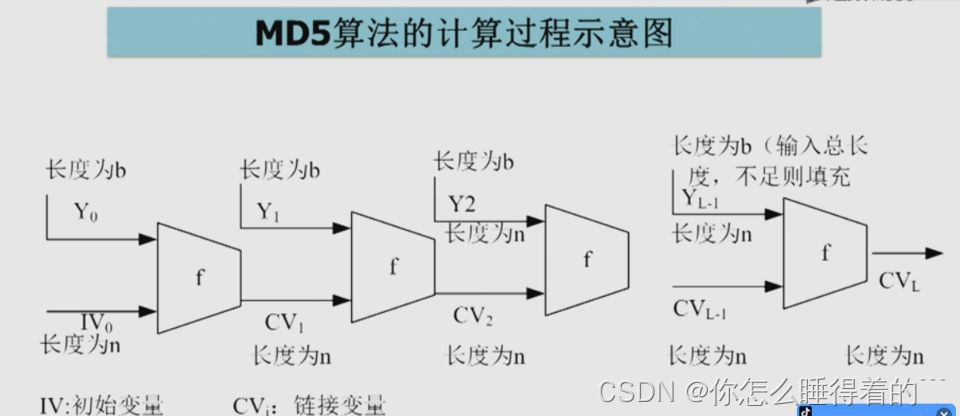

1. MD5哈希函数概述

MD5哈希函数是一种广泛使用的加密散列函数，能够产生出一个128位（16字节）的散列值（hash value），通常用一个32位的十六进制字符串表示。MD5主要被用于确保信息传输完整一致，它是密码学领域中的一种校验和散列函数，通常用于验证数据的完整性。

由于MD5的输出长度固定，使得该函数具有一定的抗碰撞性，即很难找到两个不同的输入，它们产生的散列值是相同的。尽管MD5在安全性上并不完美，例如它容易受到碰撞攻击，但其在文件完整性校验、数字签名和安全散列等领域依然有其应用。

在本章节中，我们将对MD5哈希函数进行基础性的介绍，为理解后续章节中的C++实现步骤打下坚实的理论基础。

2. C++中MD5实现的步骤

2.1 MD5实现的前期准备

2.1.1 MD5算法的基本原理

MD5（Message-Digest Algorithm 5）是一种广泛使用的密码散列函数，能产生出一个128位（16字节）的散列值（hash value），用于确保信息传输完整一致。MD5由罗纳德·李维斯特（Ronald Rivest）于1991年设计，经常用于完整性校验和验证密码等。尽管MD5比它的前辈MD4要安全一些，但现在已经发现它存在多种安全漏洞，不再被认为是安全的散列函数。MD5算法的基本原理包括：

1. 填充数据 ：确保数据块长度模512为448，如果原始数据不足以填充至512的倍数，则需要在数据后面添加一个1和相应数量的0。
2. 添加原始数据长度 ：将数据原始长度以64位填充至填充后的数据末尾。
3. 初始化MD缓冲区 ：使用四个特定的常数初始化MD缓冲区，这些常数为MD5算法的初态。
4. 处理数据 ：将填充后的数据分为512位的数据块进行处理。每个数据块都通过四个主要的函数（F, G, H, I）进行运算，产生新的MD缓冲区值。
5. 最终输出 ：将最终的MD缓冲区值输出为128位的散列值。

2.1.2 MD5实现的必要条件和工具

为了在C++中实现MD5算法，以下条件和工具是必须的：

• C++编译环境 ：一个支持标准C++的编译器，如GCC、Clang、MSVC等。
• 时间与空间复杂度 ：了解基本的时间与空间复杂度，因为MD5算法的运算效率对性能有一定影响。
• 开发库 ：一个标准库，比如标准模板库（STL）对实现MD5算法很有帮助。
• 调试与测试工具 ：调试工具和测试环境可以帮助开发者验证算法的正确性。

2.2 MD5实现的详细步骤

2.2.1 MD5核心算法的概述

MD5算法主要可以分为以下几个部分：

• 初始化MD缓冲区 ：设置初始MD缓冲区的四个分量：A、B、C、D。
• 处理消息 ：将消息分为512位的数据块，每个数据块又分为16个32位的字。
• 四个主要运算函数 ：F, G, H, I，每个函数对应不同的运算逻辑。
• 四轮操作 ：每轮分别对应不同的操作，进行16次运算。
• 输出结果 ：处理完所有数据块后，输出最终的MD缓冲区值，即为消息的MD5散列值。

2.2.2 MD5具体实现的代码分析

下面是使用C++实现MD5算法的简化代码示例，为完整实现，请查阅专门的密码学库或者相关实现代码。

#include <iostream>
#include <iomanip>
#include <sstream>

// 声明四个基本的MD5运算函数
uint32_t F(uint32_t x, uint32_t y, uint32_t z) {
    return (x & y) | (~x & z);
}

uint32_t G(uint32_t x, uint32_t y, uint32_t z) {
    return (x & z) | (y & ~z);
}

uint32_t H(uint32_t x, uint32_t y, uint32_t z) {
    return x ^ y ^ z;
}

uint32_t I(uint32_t x, uint32_t y, uint32_t z) {
    return y ^ (x | ~z);
}

// MD5散列函数实现
std::string MD5(const std::string &str) {
    // ...（此处省略了MD5算法的完整实现细节）
    return "md5结果"; // 返回计算得到的md5散列值
}

int main() {
    std::string message = "The quick brown fox jumps over the lazy dog";
    std::string hash = MD5(message);
    std::cout << "MD5(\"" << message << "\") = " << hash << std::endl;
    return 0;
}

上面的代码只是对MD5实现的简单概述，实际中需要实现所有的细节，包括数据的填充、四轮运算以及最终的散列值输出等。在实际的生产环境中，建议使用成熟的库来完成MD5算法的实现，比如OpenSSL或者Crypto++等，这样可以保证算法的正确性和安全性。

在C++中实现MD5算法需要注意各种边界情况的处理和性能优化，通常会涉及到位操作、数据结构的使用以及对特定硬件优化的代码实现。此外，实现过程中可能需要使用到一些特定的技巧和规则，比如避免编译器优化导致的运算顺序问题等。

3. 数据预处理方法

数据预处理是MD5算法中一个关键步骤，它确保输入数据符合算法处理要求。预处理不仅能够提高算法的效率，还可以确保MD5函数的安全性和可靠性。

3.1 数据预处理的目的和意义

3.1.1 数据预处理的作用

数据预处理的目的是将任意长度的原始数据转换为固定长度的比特串，以便进行MD5的后续处理。预处理包括两个主要步骤：数据填充和数据格式化。

数据填充的目的是将原始数据的长度变为512位的整数倍。这是通过在数据末尾添加一个'1'比特，后面跟随多个'0'比特，并最后添加原始数据长度的64位二进制表示完成的。填充的比特总数从64位中的第一个'0'开始计数。

3.1.2 MD5数据预处理的特殊要求

数据预处理要求算法开发者必须仔细处理每个细节，以确保数据格式的准确性。例如，数据填充操作必须精确完成，因为任何错误的填充都可能导致最终的MD5哈希值发生不可预测的变化。

3.2 数据预处理的具体实现

3.2.1 数据填充方法

数据填充的基本步骤如下：

1. 计算原始数据的长度，并将长度转换为64位的二进制数。
2. 从原始数据的末尾开始添加'1'比特，直到添加的比特数使得数据长度达到512的倍数。
3. 添加足够的'0'比特，使得填充后的数据长度比原数据长度多64位。
4. 将原始数据长度的64位二进制表示附加到填充后的数据末尾。

下面是一个数据填充的C++代码示例：

void MD5Preprocess::pad(std::vector<UInt4>& buffer, UInt8 inputLen) {
    // 计算填充后的总长度
    UInt8 paddingLen = 448 - (inputLen % 512);
    if (paddingLen < 0) paddingLen += 512; // 处理长度正好是512的倍数的情况

    // 添加填充比特'1'后跟'0'
    buffer.push_back(0x80);
    buffer.insert(buffer.end(), paddingLen / 32, 0);

    // 将输入数据长度转换为64位并添加到缓冲区
    buffer.push_back(inputLen * 8);
    buffer.push_back((inputLen * 8) >> 8);
    buffer.push_back((inputLen * 8) >> 16);
    buffer.push_back((inputLen * 8) >> 24);
    buffer.push_back((inputLen * 8) >> 32);
    buffer.push_back((inputLen * 8) >> 40);
}

3.2.2 数据格式化方法

完成数据填充之后，需要将处理好的数据分成16个小组（每组32位），这一步被称为数据格式化。数据格式化便于后续的MD5哈希计算。

这里是一个简单的示例代码，展示了如何将填充好的数据进行格式化：

std::vector<UInt4> MD5Preprocess::format(std::vector<UInt4>& buffer) {
    // 确保数据长度为512的倍数
    if (buffer.size() % 16 != 0) {
        throw std::invalid_argument("Buffer size is not a multiple of 16 after padding.");
    }

    // 按每32位一组进行分割
    std::vector<UInt4> formattedData;
    for (size_t i = 0; i < buffer.size(); i += 16) {
        std::vector<UInt4> word(16);
        for (int j = 0; j < 16; ++j) {
            word[j] = buffer[i + j];
        }
        formattedData.insert(formattedData.end(), word.begin(), word.end());
    }

    return formattedData;
}

数据预处理的步骤是确保MD5算法正确执行的基础，任何偏差都可能导致最终哈希值的不准确。通过上述步骤，我们可以确保输入数据符合MD5算法的要求，从而得到一个可靠的哈希值。

4. MD5状态初始化

4.1 MD5状态初始化的理论基础

4.1.1 MD5的四轮运算机制

MD5算法通过四轮不同的运算处理输入信息，每轮都包含16次循环，每次循环处理一个消息字。这些运算包括：非线性函数F、G、H和I，分别应用于不同的轮次。每一轮的运算基于当前状态、消息字和常数，生成一个新的状态。

每轮的运算函数如下： - 第一轮：F，对三个参数进行逻辑运算后加上第四个参数。 - 第二轮：G，对三个参数进行循环左移和按位与后加上第四个参数。 - 第三轮：H，对三个参数进行按位异或后加上第四个参数。 - 第四轮：I，对三个参数进行循环左移和按位或后加上第四个参数。

这四轮运算在算法内部通过一系列的位运算和常数加法来实现，以保证信息的混淆和扩散。

4.1.2 MD5状态初始化的必要性

在MD5算法中，状态初始化是开始哈希处理前的预备步骤，它负责设置初始的哈希值。这四个初始值是MD5算法的基础，并在后续的每一轮中被更新，它们分别是：

• A: 0x***
• B: 0xefcdab89
• C: 0x98badcfe
• D: 0x***

这些初始值是MD5算法定义的特定常数，它们在算法的每一轮中参与运算，与消息块进行复杂的操作，产生最终的哈希值。如果这些初始状态值不正确，那么最终的输出哈希值也将是错误的。

4.2 MD5状态初始化的实现方法

4.2.1 MD5初始向量的设定

MD5的初始向量设定是算法设计的一部分，这些向量是固定值，它们被直接用于算法的起始状态。在C++代码中，可以直接将这些向量定义为常量，并在状态初始化时将它们赋值给相应的状态变量。以下为设定初始向量的代码片段：

// MD5 initial hash values
uint32_t md5_initial_hash[4] = {0x***, 0xefcdab89, 0x98badcfe, 0x***};

4.2.2 MD5状态变量的初始化

在MD5算法的执行过程中，四个状态变量（A, B, C, D）将会在每一轮的运算后进行更新，初始时，将它们设置为上述定义的初始向量。初始化代码通常在MD5算法的开始处执行，以确保后续操作的正确进行。下面为状态变量初始化的代码示例：

uint32_t A = md5_initial_hash[0];
uint32_t B = md5_initial_hash[1];
uint32_t C = md5_initial_hash[2];
uint32_t D = md5_initial_hash[3];

通过以上步骤，MD5算法的状态初始化部分就完成了。在这之后，消息将被分块处理，每处理一个消息块，都会对这四个状态变量进行更新，直至所有消息块处理完毕，最终输出的就是经过MD5算法处理的摘要信息。

在接下来的章节中，我们将详细探讨MD5的迭代过程，包括四个主要运算函数的详细解析和具体实现方法。

5. MD5迭代过程的执行

5.1 MD5迭代过程的详细解析

5.1.1 MD5的四个主要运算函数

MD5算法的每个步骤都是基于四个基本的运算函数来完成的，这些函数包括：F、G、H 和 I，它们针对不同的输入数据执行位操作。这些函数作用如下：

• F(X, Y, Z) = (X AND Y) OR (NOT X AND Z)
• G(X, Y, Z) = (X AND Z) OR (Y AND NOT Z)
• H(X, Y, Z) = X XOR Y XOR Z
• I(X, Y, Z) = Y XOR (X OR NOT Z)

这些运算都是对32位整数的运算，每个函数都在不同的步骤中根据不同的输入数据（X, Y, Z）和不同的常数来执行。

5.1.2 MD5的每一步运算细节

MD5算法的迭代过程包括以下步骤：

1. 分割消息为512位的分组。
2. 对每个分组进行处理，包括填充和附加长度信息。
3. 初始化MD缓冲区，将其设置为特定的初始值。
4. 对每个512位分组执行四个轮次的处理，每个轮次都使用不同的运算函数。
5. 累加缓冲区中的值到最终的哈希值。

每一个轮次包括16个操作，这些操作涉及上述的四个基本函数F、G、H和I，以及一系列预定义的常数和对输入消息的位操作。

5.2 MD5迭代过程的代码实现

5.2.1 C++代码中如何实现MD5的迭代

为了深入理解MD5的迭代过程，下面将给出一个简化的C++代码示例，演示如何实现MD5的一个迭代过程。

#include <iostream>
#include <cstdint>
#include <iomanip>
#include <sstream>
#include <vector>

// 四个基本函数的实现
uint32_t F(uint32_t x, uint32_t y, uint32_t z) { return (x & y) | (~x & z); }
uint32_t G(uint32_t x, uint32_t y, uint32_t z) { return (x & z) | (y & ~z); }
uint32_t H(uint32_t x, uint32_t y, uint32_t z) { return x ^ y ^ z; }
uint32_t I(uint32_t x, uint32_t y, uint32_t z) { return y ^ (x | ~z); }

// 用于实现MD5的一个轮次
void md5_transform(uint32_t state[4], const uint8_t block[64]) {
    // 定义四个辅助函数
    uint32_t a = state[0], b = state[1], c = state[2], d = state[3], i;
    uint32_t x[16];

    // 填充消息块
    for (i = 0; i < 16; ++i) {
        x[i] = (block[4 * i] & 0xff) + ((block[4 * i + 1] & 0xff) << 8) + ((block[4 * i + 2] & 0xff) << 16) + ((block[4 * i + 3] & 0xff) << 24);
    }

    // MD5的四个轮次
    for (i = 0; i < 64; ++i) {
        uint32_t f, g;
        if (i < 16) {
            f = F(b, c, d);
            g = i;
        } else if (i < 32) {
            f = G(b, c, d);
            g = (5 * i + 1) % 16;
        } else if (i < 48) {
            f = H(b, c, d);
            g = (3 * i + 5) % 16;
        } else {
            f = I(b, c, d);
            g = (7 * i) % 16;
        }

        uint32_t temp = d;
        d = c;
        c = b;
        b = b + ((a + f) ^ (g + 0x5a827999));
        a = temp;
    }

    // 累加结果到当前状态
    state[0] += a;
    state[1] += b;
    state[2] += c;
    state[3] += d;
}

int main() {
    // 示例：MD5的某个消息分组和初始状态
    uint32_t state[4] = {0x***, 0x98badcfe, 0xefcdab89, 0x***};
    uint8_t block[64] = { /* 一个MD5分组的数据 */ };

    // 执行MD5的一个迭代
    md5_transform(state, block);

    // 输出结果
    for (int i = 0; i < 4; i++) {
        std::cout << std::hex << std::setw(8) << std::setfill('0') << state[i] << std::endl;
    }

    return 0;
}

5.2.2 MD5迭代过程中的常见问题及解决方法

当实现MD5时，开发者可能会遇到几个常见的问题。首先，MD5依赖于小端字节序，确保您的系统支持正确的字节序是关键。其次，循环中的位操作需要精确，任何错误都会导致不同的哈希值。还需要确保数据对齐正确，以及正确实现循环中的非线性函数和循环左移操作。

为了解决这些问题，在编程时应使用位操作原语而非组合操作，确保消息填充正确，并在测试中使用已知的测试向量来验证MD5实现的正确性。此外，针对性能优化，可以考虑使用并行处理或汇编语言优化循环。

通过以上的步骤，我们可以深入理解MD5算法中迭代过程的每一个细节，这些细节是构建完整MD5哈希函数的关键。

6. MD5摘要结果的组合

6.1 MD5摘要结果的意义

6.1.1 MD5摘要结果的特点

MD5摘要结果是由128位的哈希值组成，具有以下特点：

1. 唯一性 ：理论上不同的输入数据将产生不同的哈希值，然而由于哈希冲突的存在，这一点无法保证。
2. 固定长度 ：无论输入数据的大小，MD5摘要结果始终是128位（即16字节）。
3. 不可逆性 ：从MD5摘要结果很难反推出原始数据，这为信息加密和安全验证提供了基础。

6.1.2 MD5摘要结果的应用场景

MD5摘要结果广泛应用于数据完整性校验、密码存储、数字签名等领域。例如：

• 在软件下载中，开发者会提供文件的MD5哈希值，用户下载后可以通过计算哈希值来验证文件的完整性。
• 在系统认证中，用户的密码在存储时并不直接存储明文，而是存储其MD5摘要结果，这样即使数据库被泄露，攻击者也无法直接获取用户密码。
• 在数字签名中，MD5摘要结果用于确保数据在传输过程中未被篡改。

6.2 MD5摘要结果的生成与输出

6.2.1 MD5摘要结果的组合步骤

MD5摘要结果的生成涉及到将四个32位变量（A、B、C、D）进行组合，最终生成128位的哈希值。组合步骤通常如下：

1. 最终连接（Finalization） ：将MD5算法的四个状态变量A、B、C、D的值按照一定的顺序拼接起来。
2. 输出格式化 ：由于MD5设计时希望输出的哈希值是32个十六进制字符，因此需要将最终的128位数据转换为32个十六进制字符。

6.2.2 MD5摘要结果的最终输出形式

MD5摘要结果的输出形式通常是32个十六进制字符，例如：

4a6e89b5a1c9f4f1d5e53b6a1f17f5e9

在实际应用中，这32个字符通常会被分组显示，每组四个字符，方便阅读和校验。例如：

4a6e 89b5 a1c9 f4f1 d5e5 3b6a 1f17 f5e9

MD5摘要结果提供了数据验证和完整性校验的强大工具，虽然它已经不再被认为是安全的加密哈希算法，但在许多非安全性的应用场景中，MD5摘要结果仍然有其用武之地。

注意：在安全性要求高的场景中，MD5已经被更安全的算法，如SHA-256等取代。MD5算法由于其设计中的弱点，容易受到碰撞攻击，不再推荐用于安全加密。

7. C++ MD5代码的实用技巧与注意事项

在上一章中，我们详细地探讨了MD5摘要结果的生成与输出。现在让我们把焦点放在实践中会遇到的一些技巧和注意事项上，尤其是在C++中使用MD5算法时。

7.1 使用openssl库简化MD5实现

在C++中实现MD5算法，开发者可以利用现有的库来简化这一过程，其中openssl库就是一个强大的选择。openssl不仅提供了多种加密算法的实现，而且因其稳定性和广泛支持而被许多项目采纳。

7.1.1 openssl库的基本介绍

openssl是一个开源的加密库，包含了一系列广泛用于加密通信的工具和库函数。它支持SSL/TLS和安全通信协议，并提供了包括MD5在内的多种哈希函数的实现。openssl库广泛应用于Linux、Windows、macOS等操作系统。

7.1.2 如何在C++中集成openssl库实现MD5

要使用openssl库实现MD5，首先需要安装openssl开发库，并在项目中正确地引入头文件和链接库。

下面是一个简单的示例代码：

#include <iostream>
#include <openssl/md5.h>

int main() {
    const char *text = "Hello, World!";
    unsigned char digest[MD5_DIGEST_LENGTH];
    MD5_CTX c;
    MD5_Init(&c);
    MD5_Update(&c, text, strlen(text));
    MD5_Final(digest, &c);

    for(int i = 0; i < MD5_DIGEST_LENGTH; i++)
        printf("%02x", digest[i]);
    printf("\n");
    return 0;
}

在此代码中， MD5_CTX 是存储MD5上下文信息的结构体。 MD5_Init 、 MD5_Update 和 MD5_Final 是用于初始化、更新和获取最终哈希值的函数。 MD5_DIGEST_LENGTH 是MD5哈希值的长度（16字节）。

7.2 MD5代码编译和运行的注意事项

在编译使用了openssl库的MD5代码时，需要确保正确链接openssl库。

7.2.1 MD5代码的编译技巧

如果使用g++进行编译，可以通过添加 -lssl -lcrypto 选项来链接所需的库：

g++ -o md5_example md5_example.cpp -lssl -lcrypto

7.2.2 MD5代码运行时的常见错误及预防

当运行上述编译好的程序时，可能会出现库找不到的错误，如 error while loading shared libraries: libssl.so.1.1 。这时需要设置环境变量 LD_LIBRARY_PATH ，或者将库文件放置到系统库目录中。

7.3 内存管理与错误处理

管理好内存使用和适当的错误处理对于编写健壮的C++代码非常重要。

7.3.1 代码中的内存管理方法

在使用openssl的MD5函数时，通常不需要手动管理内存，因为这些函数使用栈上的局部变量。但是，在处理更复杂的数据结构时，应遵循RAII（资源获取即初始化）原则。

7.3.2 MD5实现中的错误处理机制

openssl的MD5函数在失败时返回错误代码。合理地检查这些错误代码并给出适当的错误处理是非常重要的。

7.4 编码兼容性与代码组织

在不同的开发环境中保持代码兼容性以及组织良好的代码，可以提高代码的可维护性和可读性。

7.4.1 MD5代码在不同平台的兼容性问题

openssl提供了跨平台的头文件，通常情况下，直接使用它不会出现兼容性问题。然而，有时可能需要确保使用的是与系统匹配的库版本。

7.4.2 优化MD5代码的结构与可读性

清晰地组织代码，使用恰当的变量和函数命名，为MD5相关的操作编写清晰的注释，可以大大提升代码的可读性。此外，可以将MD5的实现封装在类或命名空间中，以隔离实现细节。

通过以上章节的讨论，我们了解了在C++中实现MD5时可能会遇到的问题以及对应的解决方案，这将有助于我们在实际项目中更高效地使用MD5算法。

本文还有配套的精品资源，点击获取

简介：MD5是一种广泛使用的哈希函数，用于将任意长度的数据转换为固定长度的128位摘要。本文提供了在C++中实现MD5算法的详细步骤，包括数据预处理、初始化状态、执行迭代过程和组合结果。同时，介绍了如何使用openssl库简化实现过程，以及在DEV环境下编译和运行MD5代码时应注意的内存管理、错误处理、编码兼容性和代码组织问题。MD5的实现是理解哈希算法和提高编程技能的重要实践。

本文还有配套的精品资源，点击获取