动态规划之最长公共子序列

最新推荐文章于 2023-06-01 19:25:01 发布
最新推荐文章于 2023-06-01 19:25:01 发布
阅读量102 收藏
点赞数
文章标签： 数据结构与算法 java
原文链接：http://www.cnblogs.com/mrzhang123/p/5365805.html
版权

这个世界上根本就不存在“不会做”这回事，当你失去了所有的依靠的时候，自然就什么都会了。

0. 前言

　　最长公共子序列的问题常用于解决字符串的相似度，是一个非常实用的算法，作为码农，此算法是我们的必备基本功。最长公共子串（Longest Common Substirng）和最长公共子序列（Longest Common Subsequence，LCS）的区别为：子串是串的一个连续的部分，子序列则是从不改变序列的顺序，而从序列中去掉任意的元素而获得新的序列；也就是说，子串中字符的位置必须是连续的，子序列则可以不必连续。

1.最长公共子序列概述

　　问题描述: 字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列X=“x0，x1，…，xm-1”，序列Y=“y0，y1，…，yk-1”是X的子序列，存在X的一个严格递增下标序列

2. 动态规划求解最长公共子序列　　

2.1 刻画最长公共子序列的最优子结构的特征

　　如果使用暴力搜索求解LCS问题，需要穷举X的所有子序列，对每一个子序列检查它是否是Y的子序列，记录找到的最长的子序列。X的每个子序列对应的X的下标集合是(1,2,3,.....m)的一个子集，所以有2m个子序列。但是最长公共子序列有最优子结构的性质。子问题的自然分类对应两个输入序列的“前缀”对。
　　定理： 考虑最长公共子序列问题如何分解成子问题，设A=“a1，…，am”，B=“b1，…，bn”，并Z=“z1，…，zk”为它们的最长公共子序列。不难证明有以下性质：
（1） 如果am=bn，则zk=am=bn，且“z1，…，zk-1”是“a1，…，am-1”和“b1，…，bn-1”的一个最长公共子序列；
（2） 如果am!=bn，则若zk!=am，蕴涵“z1，…，zk”是“a1，…，am-1”和“b1，…，bn”的一个最长公共子序列；
（3） 如果am!=bn，则若zk!=bn，蕴涵“z1，…，zk”是“a1，…，am”和“b1，…，bn-1”的一个最长公共子序列。
　　上面的定理告诉我们：两个序列的LCS包含两个序列前缀的LCS，因此LCS问题具有最优子结构的性质。

2.2 构建递归解

　　通过上面的定理我们可以发现在求A=“a1，…，am”，B=“b1，…，bn”的一个公共的LCS的时候我们需要求解一个到两个子问题。、
　　【1】如果am=bn，我们应该求Am−1和Bn−1的LCS；
　　【2】如果am!=bn，若zk!=am，我们应该求Am−1和Bn的LCS。如果am!=bn，则若zk!=bn，我们应该求Am和Bn−1的LCS。两者LCS比较长的称为A和B的LCS。
　　我们可以很容易的发现子问题重叠的性质。在求A和B的LCS的过程中，我们的2种情况，都存在Am−1和Bn−1的LCS的重叠子问题。设计LCS的递归算法首先需要建立最优解的递归式，C[i,j]表示Ai和Bj的LCS长度，如果i=j=0,那么c[i,j]=0.根据LCS问题最优子结构的性质得出以下公式：
　　

c[i,j]=⎧⎩⎨　　0　　c[i−1,j−1]+1　　max(c[i,j−1],c[i−1,j])若i=0或者j=0若i,j>0 且 Ai = Bj若i,j>0 且Ai!=Bj　　

　　 在上面的问题中我们通过限制条件限定了需要求解哪些子问题。在前面的算法中我们没有限定排除任何子问题，在这里我们需要根据限制条件排除相应的子问题。
2.3 计算LCS的长度（求最优解）

根据2.2的递归公式，我们可以很痛以的写出一个指数时间的递归算法。但是，由于LCS问题只有Θ(mn)个不同的子问题，我们可以使用DP来自底向上的计算。
算法伪代码：

LCS-Length(X[],Y[]){
    int m=x.length;
    int n=Y.length;
    int[][] c = new int[m + 1][n + 1];
    char[][] b = new char[m + 1][n + 1];

    for(i=1 to m){
        c[i,0]=0;//
    }
    for(j=0 to n){
        c[0,j]=0;
    }
    /**
    i是行 j是列
    */
    for(i=1 to m){
        for(j=1 to n){
            if(xi==yj){
                c[i,j]=c[i-1,j-1]+1;
                b[i,j]='\';
            }
            elseif(c[i-1,j]>=c[i,j-1]){
                c[i,j]=c[i-1,j];
                b[i,j]='|';
            }else{
                c[i,j]=c[i,j-1];
                b[i,j]='--';
            }
        }
    }

    return c and b;


}
2.4 构造LCS（构造最优解）

我们可以使用辅助表b来快速构造x和y的LCS，只需要从b[m,n]开始按照箭头的方向追踪即可.递归算法如下：

PRINT_LCS(X,b[][],i,j){
    if(i==0 || j==0){
        return;
    }
    if(b[i,j]=="\"){
        PRINT_LCS(X,b[][],i-1,j-1);
        print xi;
    }else if(b[i,j]=="|"){
        PRINT_LCS(X,b[][],i-1,j)
    }else{
        PRINT_LCS(X,b[][],i,j-1)
    }

}

3. 动态规划Java实现　　

算法实现类

package lbz.ch15.dp.ins3;

/**
 * @author LbZhang
 * @version 创建时间：2016年3月9日 下午9:51:22
 * @description 最大公共子序列
 */
public class LCS {
    /***
     * * 这一部分我们使用辅助表，从左上角开始计算每一个位置上LCS的长度 判断算法：
     */
    public static int[][] lcsLength(Object[] x, Object[] y) {
        int m = x.length;
        int n = y.length;

        int[][] c = new int[m + 1][n + 1];
        char[][] b = new char[m + 1][n + 1];
        int i, j;
        for (i = 1; i <= m; i++) {
            c[i][0] = 0;
        }
        for (j = 0; j <= n; j++) {
            c[0][j] = 0;
        }
        for (i = 1; i <= m; i++) {
            for (j = 1; j <= n; j++) {
                if (x[i - 1].equals(y[j - 1])) {
                    c[i][j] = c[i - 1][j - 1] + 1;
                    b[i][j]='\\';
                } else if (c[i - 1][j] >= c[i][j - 1]) {
                    c[i][j] = c[i - 1][j];
                    b[i][j]='|';
                } else {
                    c[i][j] = c[i][j - 1];
                    b[i][j]='-';
                }
            }
        }
        return c;
    }
    /**
     * 为了输出最长公共子序列，改进的输出
     * @param x
     * @param y
     * @return
     */

    public static char[][] lcsPrint(Object[] x, Object[] y) {
        int m = x.length;
        int n = y.length;

        int[][] c = new int[m + 1][n + 1];
        char[][] b = new char[m + 1][n + 1];
        int i, j;
        for (i = 1; i <= m; i++) {
            c[i][0] = 0;
        }
        for (j = 0; j <= n; j++) {
            c[0][j] = 0;
        }
        for (i = 1; i <= m; i++) {
            for (j = 1; j <= n; j++) {
                if (x[i - 1].equals(y[j - 1])) {
                    c[i][j] = c[i - 1][j - 1] + 1;
                    b[i][j]='\\';
                } else if (c[i - 1][j] >= c[i][j - 1]) {
                    c[i][j] = c[i - 1][j];
                    b[i][j]='|';
                } else {
                    c[i][j] = c[i][j - 1];
                    b[i][j]='-';
                }
            }
        }
        return b;
    }

    // ///print the lcs
    // //采用递归的方式将结果打印出来
    public static void printLcs(int[][] c, Object[] x, Object[] y, int i, int j) {
        if (i == 0 || j == 0) {
            return;
        }
        if (x[i - 1].equals(y[j - 1])) {
            printLcs(c, x, y, i - 1, j - 1);
            System.out.print(x[i - 1] + " ");
        } else if (c[i - 1][j] >= c[i][j - 1]) {
            printLcs(c, x, y, i - 1, j);
        } else {
            printLcs(c, x, y, i, j - 1);
        }
    }

    public static void printBySignalLcs(char[][] b, Object[] x, int i, int j) {
        if (i == 0 || j == 0) {
            return;
        }
        if (b[i][j]=='\\') {
            printBySignalLcs(b,x,i-1,j-1);
            System.out.print(x[i - 1] + " ");
        } else if (b[i][j]=='|') {
            printBySignalLcs(b,x,i-1,j);
        } else {
            printBySignalLcs(b,x,i,j-1);
        }
    }
}

测试类

package lbz.ch15.dp.ins3;
/** 
 * @author LbZhang
 * @version 创建时间：2016年3月10日 下午3:19:57 
 * @description 最长公共子序列测试类
 */
public class Test {
    public static void main(String[] args) {
        Character[] x = { 'A', 'C', 'C', 'G', 'G', 'T', 'C', 'G', 'A', 'G',
                'T', 'G', 'C', 'G', 'C', 'G', 'G', 'A', 'A', 'G', 'C', 'C',
                'G', 'G', 'C', 'C', 'G', 'A', 'A' }, 
                y = { 'G', 'T', 'C', 'G',
                'T', 'T', 'C', 'G', 'G', 'A', 'A', 'T', 'G', 'C', 'C', 'G',
                'T', 'T', 'G', 'C', 'T', 'C', 'T', 'G', 'T', 'A', 'A', 'A' };
        Integer[] a = { 389, 207, 155, 300, 299, 170, 158, 65 }, b = { 389,
                300, 299, 207, 170, 158, 155, 65 };

        int[][] c;
        char[][] p;
        c = LCS.lcsLength(x, y);
        //p=LCS.lcsPrint(x, y);
        LCS.printLcs(c, x, y, 29, 28);
        System.out.println();
        c = LCS.lcsLength(a, b);//二维表
        LCS.printLcs(c, a, b, 8, 8);
        System.out.println();

        System.out.println("--------******改进******---------");
        p=LCS.lcsPrint(x, y);
        LCS.printBySignalLcs(p, x, 29, 28);
        System.out.println();
        p=LCS.lcsPrint(a, b);
        LCS.printBySignalLcs(p, a, 8, 8);
    }

}

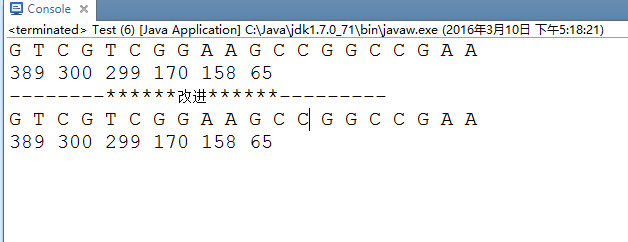
实验结果
最大公共子序列

转载于:https://www.cnblogs.com/mrzhang123/p/5365805.html

最长公共子序列问题
zijiaobingbu的专栏
11-14 2168
最长公共子序列问题（LCS）（生物信息学中常用算法） 子序列的概念：   设X = 1,x2,┅, xm>，若有1≤i12k≤m，使得Z=1, z2,┅, zk> =i1, xi2,┅, xik>，则称Z是X的子序列，记为Z, Z=,  则有Z 公共子序列的概念： 设X，Y是两个序列，且有Z 最长公共子序列的概念：若Z 最长公共子序列往往不止一个。e.g. X=, Y=, 则Z=,
【动态规划专题】最长公共子序列问题
ghscarecrow的博客
04-07 493
最长子序列问题（longest -common-subsequence problem）是一个经典的体现动态规划思想的算法问题，问题描述如下：给定两个子序列X={x1,x2,x3...xm}和Y={y1,y2,y3,...yn}。求X和Y长度最长的公共子序列。对于该问题，倘若我们使用暴力搜索法进行求解，无疑就需要穷举X的所有子序列。然后对每一个子序列检查它是否也是Y的子序列，记录找到最长的子序列。...
最长公共子序列
WILL的专栏
03-01 733
最长公共子序列问题LCS 问题描述 参考解答 动态规划算法可有效地解此问题。下面我们按照动态规划算法设计的各个步骤来设计一个解此问题的有效算法。 1.最长公共子序列的结构 解最长公共子序列问题时最容易想到的算法是穷举搜索法，即对X的每一个子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列，并且在检查过程中选出最长的公共子序列。X的所有子序列都检查过后即可求出X和
动态规划解最长公共子序列(LCS)(附详细填表过程)
z-k的博客
11-20 15万+
目录 相关概念 子序列形式化定义： 公共子序列定义： 最长公共子序列（以下简称LCS）： 方法 蛮力法求解最长公共子序列： 动态规划求解最长公共子序列： 分析规律： 做法： 伪代码： 下面演示下c数组的填表过程：（以求ABCB和BDCA的LCS长度为例）： 时间复杂度： 代码： 结果示例： 相关概念 子序列形式化定义： 给定一个序列X=<x1,x2,x3,x...
动态规划 最长公共子序列 过程图解
热门推荐
hrn1216的博客
05-29 28万+
1.基本概念       首先需要科普一下，最长公共子序列（longest common sequence）和最长公共子串（longest common substring）不是一回事儿。什么是子序列呢？即一个给定的序列的子序列，就是将给定序列中零个或多个元素去掉之后得到的结果。什么是子串呢？给定串中任意个连续的字符组成的子序列称为该串的子串。给一个图再解释一下：        如
算法设计与分析实验报告-动态规划寻找最长公共子序列.doc
12-11
总的来说，动态规划在解决最长公共子序列问题时展现了其强大之处，通过优化算法设计，避免了指数级的时间复杂度，实现了线性时间复杂度的高效解决方案。实验报告不仅提升了对动态规划的理解，还锻炼了编程实现和问题...
动态规划之最长公共子序列代码（java）
m0_58943061的博客
10-17 1056
动态规划之最长公共子序列代码（java）
动态规划之最长公共子序列LCS
Tom_JO的博客
06-05 307
动态规划之最长公共子序列LCS
最长公共子序列问题LCS
05-18
最长公共子序列问题LCS,有原码，以及说明部分
最长公共子序列——LCS
wzzzj的博客
04-27 276
首先要知道什么是子序列?它和子串的区别： 子串是指字符串中连续的n个字符。 子序列是指字符串中不一定连续但先后顺序不变的n个字符。 公共子序列是指在两个字符串中都含有的子序列，例如：asgpdf aosfdp 这两个字符串都包含子序列asf(asd,asp)等，并且这三个是最长的公共子序列，所以LCS并不是唯一的，但LCS的长度肯定是一定的（废话…）。 这是一个动态规划的题目。对于可用动态规划求解...
3.3 最长公共子序列
最新发布
tang7mj的博客
06-01 2449
我的理解：在字符串或序列中，子序列是指从原始序列中删除零个或多个元素后得到的序列，而且相对顺序保持不变。换句话说，子序列是从原始序列中选择出的元素，它们保持相对顺序，但可以跳过一些元素或者不选择任何元素。举个例子，考虑序列 "abcd"，它的一些子序列包括："a"，"b"，"c"，"d"，"ab"，"ac"，"ad"，"bc"，"bd"，"cd"，"abc"，"abd"，"acd"，"bcd"，"abcd"。注意，这些子序列可能不一定是连续的，可以跳过某些元素。
最长公共子序列-动态规划
迷雾总会解
07-02 2236
定义描述  若给定序列X={x1x_1x1​,x2x_2x2​,…,xmx_mxm​}，则另一序列Z={z1z_1z1​,z2z_2z2​,…,zkz_kzk​} 是X的子序列，是指存在一个严格递增下标序列{i1i_1i1​,i2i_2i2​,…,iki_kik​}使得对于所有j=1,2,…,k有：zjz_jzj​ = xijx_{i_j}xij​​ 。  例如，序列Z={B，C，D，B}是序列X={A，B，C，B，D，A，B}的子序列，相应的递增下标序列为{2，3，5，7}  给定2个序列X和Y，当另
数据结构 : 动态规划学习三 | 最长公共子序列
【黑键】
01-19 244
动态规划学习三 | 最长公共子序列 动态规划 之 最长公共子序列 过程图 求最长公共子序列的长度 倒推构造最长公共子序列 算法推导:动态规划算法解最长公共子序列LCS问题 记: Xi=﹤x1，⋯，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀） Yj=﹤y1，⋯，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀） 假设: Z=﹤z1，⋯，zk﹥∈LCS(X , Y) 若xm=yn（最...
经典算法——最长公共子序列
lsh199196的专栏
04-27 1081
最长公共子序列问题-LCS问题问题描述：给定两个序列 X={x1,x2,x3,…,xm}和Y={y1,y2,…,yn}，求X和Y长度最长的公共子序列。求解思路： 寻找特征: LCS问题具有最优子结构性质。可以将子问题对应两个输入序列的前缀对。 令Z = {z1,z2,…,zk}，为X和Y的任意LCS。有如下性质， 1.1 如果xm = yn,则zk = xm = yn 且Zk-1是Xm-1和Y
【算法设计与分析】最长公共子序列问题 动态规划算法 超详细
寒泉
04-29 3万+
最长公共子序列问题描述 运行效果 调试中的一个过程截取 单步填写之后 …其余中间过程省略 最终执行结果↓ 输出：BDFI 代码 #include<iostream> #include<cstring> using namespace std; int c[10][7];//Xi Yj的最长公共子序列的长度 int s[10][7];//c[i][j]的值是由...
通俗理解动态规划：由浅入深DP并解决LCS问题(23年修订版)
结构之法 算法之道
12-31 11万+
动态规划算法解LCS问题作者 July 二零一零年十二月三十一日本文参考：微软面试100题系列V0.1版第19、56题、算法导论、维基百科。第一部分、什么是动态规划算法 ok，咱们先来了解下什么是动态规划算法。 动态规划一般也只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足，故有时需要引入一定的近似)。简单地说，问题能
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值