内部排序算法的性能分析_时间复杂度的分析及排序算法总结

时间复杂度

当问题规模即要处理的数据增⻓时，基本操作要重复执⾏的次数必定也会增⻓，那么我们关⼼地是这个执⾏次数以什么样的数量级增⻓。

算法时间复杂度是一个函数，它定性描述该算法的运行时间(也就是所花费时间的消耗)。

我们要知道讨论的时间复杂度就是指一般情况下的时间复杂度。

表示法

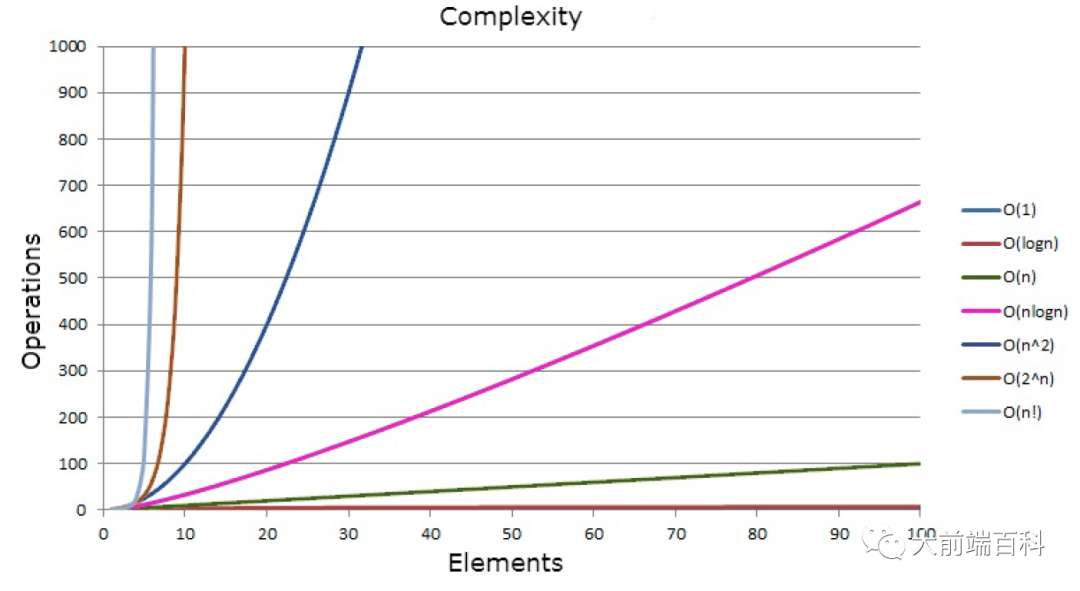
我们⽤⼤O表示法表示⼀下常⻅的时间复杂度量级：

常数阶O(1) 线性阶O(n) 对数阶O(logn) 线性对数阶O(nlogn) 平⽅阶O(n²)。

排序算法中各个算法时间复杂度为：O(n²), O(nlogn), O(n)。这些我们之前都学习过，可以先从排序算法来理解时间复杂度。这里所说的都是指的一般情况下的时间复杂度(或者平均时间复杂度)。

当然还有指数阶和阶乘阶这种⾮常极端的复杂度量级，我们就不讨论了。

O(1)

传说中的常数阶的复杂度，这种复杂度⽆论数据规模n如何增⻓，计算时间是不变的。不管n如何增⻓，都不会影响到这个函数的计算时间，因此这个代码的时间复杂度都是O(1)。

O(n)

线性复杂度，随着数据规模n的增⻓，计算时间也会随着n线性增⻓。典型的O(n)的例⼦就是线性查找。

const linearSearch = (arr, target) => {  for (let i = 0; i < arr.length; i++) {    if (arr[i] === target) {      return i;    }  }  return -1;}

线性查找的时间消化与输⼊的数组数量n成⼀个线性⽐例，随着n规模的增⼤，时间也会线性增⻓。

注意：下面代码的时间复杂度也是O(n)。

O(n + n) = O(2n) = O(n)。

const search = (arr) => {  for (let i = 0; i < arr.length; i++) {    ...  }    for (let i = 0; i < arr.length; i++) {    ...  }      return -1;}

O(logn)

对数复杂度，随着问题规模n的增⻓，计算时间也会随着n对数级增⻓。

典型的例⼦是⼆分查找法(有序序列)。

functions binarySearch(arr, target) {    let max = arr.length - 1；    let min = 0；        while (min <= max) {        let mid = Math.floor((max + min) / 2)；        if (target < arr[mid]) {                max = mid - 1；        } else if (target > arr[mid]) {                min = mid + 1；        } else {            return mid；            }    }    return -1}

在⼆分查找法的代码中，通过while循环，成 2 倍数的缩减搜索范围，也就是说需要经过 log₂n 次即可跳出循环。

事实上在实际项⽬中， O(logn) 是⼀个⾮常好的时间复杂度，⽐如当 n=100 的数据规模时，⼆分查找只需要7次，线性查找需要100次，这对于计算机⽽⾔差距不⼤，但是当有10亿的数据规模的时候，⼆分查找依然只需要30次，⽽线性查找需要惊⼈的10亿次， O(logn) 时间复杂度的算法随着数据规模的增⼤，它的优势就越明显。

O(nlogn)

线性对数复杂度，随着数据规模n的增⻓，计算时间也会随着n呈线性对数级增⻓。

这其中典型代表就是归并排序，快速排序，堆排序，希尔排序。

以堆排序为例：

堆排序中有两个步骤：

1. 创建堆：

2. 调整堆

O(n²)

平⽅级复杂度，典型情况是当存在双重循环的时候，即把 O(n) 的代码再嵌套循环⼀遍，它的时间复杂度就是 O(n²)了，代表应⽤是冒泡排序，插入排序，简单选择排序。

注意：要理解时间复杂度本质，不能单纯的记忆两个for循环的时间复杂度是O(n²)，三个for循环的时间复杂度是O(n³)，还要看for循环的数量级。例如希尔排序，是三个for循环，但是它的时间复杂度是O(nlogn)。

关于logn思考

logn指的是n的对数，在数学中，n的对数必须有底数，也就是像log₂n，log₃n...。

那时间复杂度中的logn是以几为底数呢？

有人说logn的底数为2，这种理解非常的片面，可以说是很不准确的，说明还没有理解时间复杂度所要表达的本质是什么。看了一些文档，但是并没有看到一篇好的文章去说明，或者探讨清楚这个问题。实际上无论以2，或3为底数，其实这些都是常量，并不影响我们用logn来表述算法的时间复杂度，就像两个n数量级的for循环一样，并不是O(2n)，而是O(n)。所以，我们统一说是O(logn)，也就是忽略了底数的描述。

推导：(以2，和10为例)

1. n = ₁₀ log₁₀n

2. log₂n = log₁₀n * log₂10

3. log₂n  => log₁₀n

递归算法的时间复杂度

相信很多同学对递归算法的时间复杂度都很模糊。

「同一道题目，同样使用递归算法，有的同学会写出了O(n)的代码，有的同学就写出了O(logn)的代码」。

这是为什么呢？如果对递归的时间复杂度理解的不够深入的话，就会这样！递归代码看起来很简介，优雅，但理解起来不是很透彻，包括我有些地方也不是很透彻，那在使用的过程中就更不容易用好递归了。

一个例子，来带大家逐步分析递归算法的时间复杂度，最后找出最优解，来看看同样是递归，怎么就写成了O(n)的代码。

求x的n次方

function func1(x, n) {    let result = 1;  // 注意 任何数的0次方等于1    for (let i = 0; i < n; i++) {        result = result * x;    }      return result;}

上面的代码的时间复杂度为O(n)，怎么能把上面的代码优化一下，降低时间复杂度呢？

用递归实现

function func2(x, n) {    if(n == 0){       return 1;    }      return x * func2(x, n-1);}

递归算法的时间复杂度本质上是要看: 「递归的次数 * 每次递归中的操作次数」。

所以上面代码的时间复杂度是 O(n)，并没有得到优化。

另一种递归实现

function func3(x, n){    if(n== 0) {        return 1;    }    if(n % 2 === 1) {        let n1 = Math.floor(n/2);        return func3(x, n1) * func3(x, n1) * x;    }    return func3(x, n/2) * func3(x, n/2); }

我们来分析一下，首先看递归了多少次呢，可以把递归抽象出一颗满二叉树。刚刚同学写的这个算法，可以用一颗满二叉树来表示(为了方便表示，选择n为偶数16)，如图：

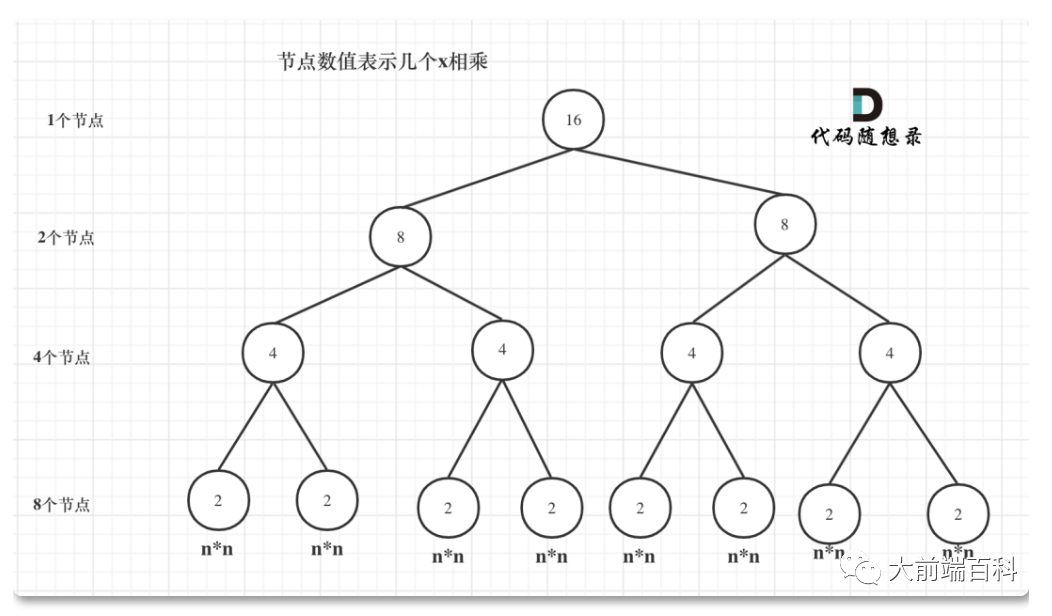
这棵树上每一个节点就代表着一次递归并进行了一次相乘操作，所以进行了多少次递归的话，就是看这棵树上有多少个节点。

熟悉二叉树话应该知道如何求满二叉树节点数量，这颗满二叉树的节点数量就是2^3 + 2^2 + 2^1 + 2^0 = 15，可以发现：「这其实是等比数列的求和公式，这个结论在二叉树里也经常出现」。

这么如果是求x的n次方，这个递归树有多少个节点呢？

「时间复杂度忽略掉常数项-1之后，这个递归算法的时间复杂度依然是O(n)」。对，你没看错，依然是O(n)的时间复杂度！

看来还是没有得到优化啊。返回看func3中存在很多重复的递归计算，可以从这个点进行优化。

第三种递归实现

function func4(x, n){    if(n== 0) {        return 1;    }    let t = func4(x, Math.floor(n/2));    if(n % 2 === 1) {        return t * t * x;    }    return t * t; }

依然还是看他递归了多少次，可以看到这里仅仅有一个递归调用，且每次都是n/2 ，所以这里我们一共调用了log以2为底n的对数次。

所以，上面的算法时间复杂度为O(logn).

同样使用递归，有的人可以写出O(logn)的代码，有的人还是可以写出O(n)的代码。

相信大家对递归算法的有一个新的认识的，同一个问题，同样是递归，效率可是不一样的！

还能不能再优化呢？就是想让递归的执行时间缩短！！

第四种递归实现

function func5(x, n, res){   if(n == 1) {     return res;   }   return func5(x, n-1, res*x);}

上面的递归实现，代码简洁了很多，可读性也好了很多，但是看不出来性能哪里好了？执行时间呢？

下面将第三种递归和第四种递归做一个执行时间的对比：

function func4(x, n){    if(n== 0) {        return 1;    }    let t = func4(x, Math.floor(n/2));    if(n % 2 === 1) {        return t * t * x;    }    return t * t; }function func5(x, n, res){   if(n == 1) {     return res;   }   return func5(x, n-1, res*x);

}

console.time();

console.log(func4(2, 100));

console.timeEnd();

console.time();

console.log(func5(2, 100, 2));

console.timeEnd();

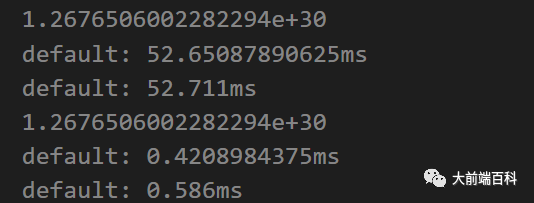
我地个天啊，差距怎么这么大啊！！最后一种递归的实现怎么竟然可以这么的优秀！！！这个会在我的另一篇文章中招到答案。

至此，希望大家对时间复杂度有一个初步的理解和认识。

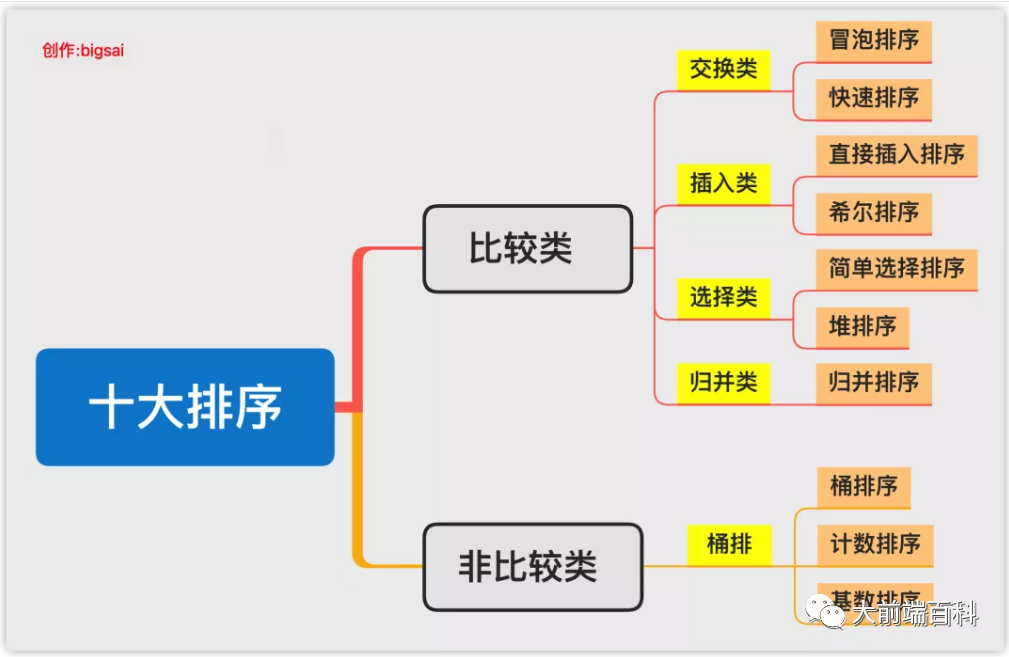
排序算法总结

排序算法比较

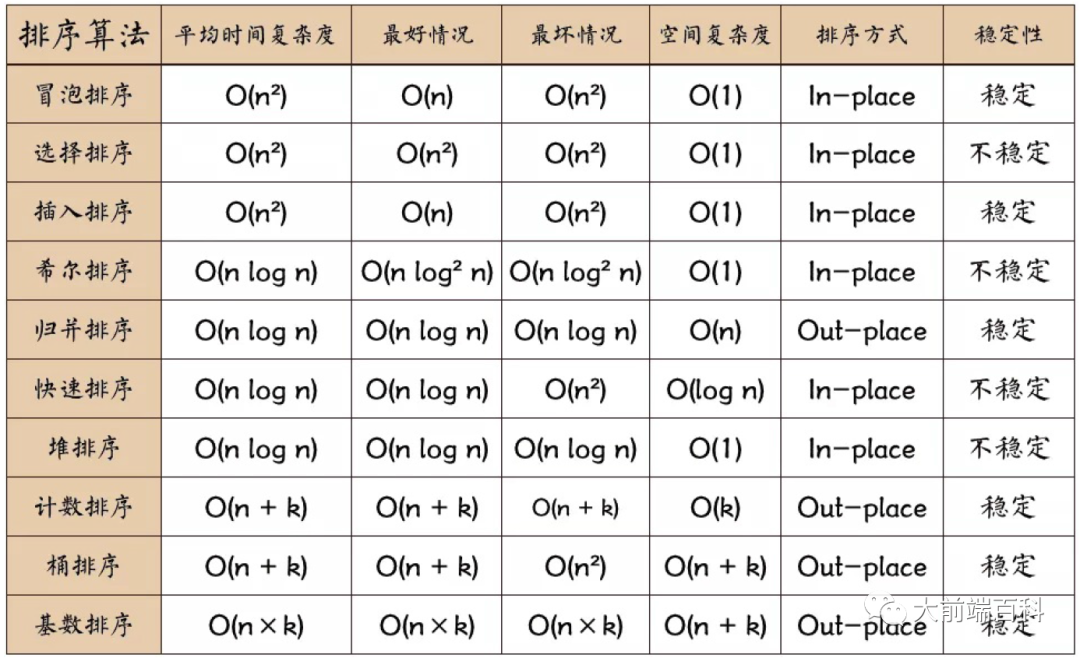
排序算法的选择

不同算法的时间复杂度 在不同数据输入规模下的差异。

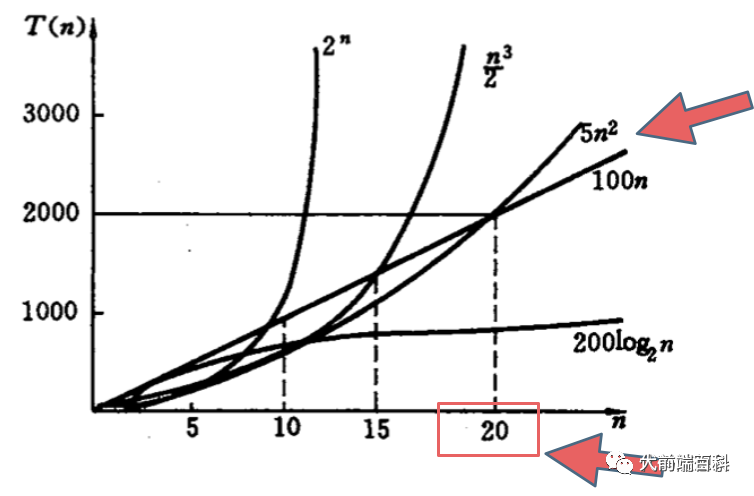
我们在决定使用那些算法的时候 ，不是时间复杂越低的越好，要考虑数据规模，如果数据规模很小可以用O(n^2)的算法。

就像上图中图中 O(5n^2) 和 O(100n) 在n为20之前 很明显 O(5n^2)是更优的，所花费的时间也是最少的。

这也就是为什么JS中自带排序方法 Array.sort在数据量小的情况下，选择插入排序的原因。