图论算法

五一时候随便翻书看到了一些关于离散数学图论的模板和算法，大概总结了一下，图论要比数论稍简单一点点。。。

一、
　　点用边连起来就叫做图，严格意义上讲，图是一种数据结构，定义为：graph=（V，E）。V是一个非空有限集合，代表顶点（结点），E代表边的集合。
二、图的一些定义和概念
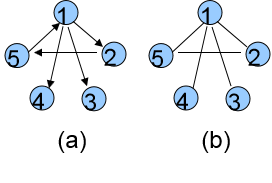
(a)有向图：图的边有方向，只能按箭头方向从一点到另一点。(a)就是一个有向图。
(b)无向图：图的边没有方向，可以双向。(b)就是一个无向图。
结点的度：无向图中与结点相连的边的数目，称为结点的度。
结点的入度：在有向图中，以这个结点为终点的有向边的数目。结点的出度：在有向图中，以这个结点为起点的有向边的数目。   

 

                              

权值：边的“费用”，可以形象地理解为边的长度。
连通：如果图中结点U，V之间存在一条从U通过若干条边、点到达V的通路，则称U、V 是连通的。
回路：起点和终点相同的路径，称为回路，或“环”。
完全图：一个n 阶的完全无向图含有n*(n-1)/2 条边；一个n 阶的完全有向图含有n*(n-1)条边；

　　　　稠密图：一个边数接近完全图的图。
　　　　稀疏图：一个边数远远少于完全图的图。
　　　　
强连通分量：有向图中任意两点都连通的最大子图。右图中，1-2-5构成一个强连通分量。特殊地，单个点也算一个强连通分量，所以右图有三个强连通分量：1-2-5，4，3。

• 图的存储结构

1.二维数组邻接矩阵存储
定义int  G[101][101];
G[i][j]的值，表示从点i到点j的边的权值，定义如下：

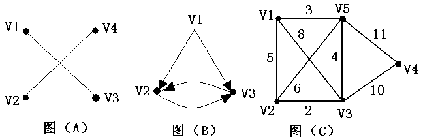
                0  1  1  1                     0  1  1                    
G（A）=   1  0  1  1    G（B）=    0  0  1                    
　　          1  1  0  0                     0  1  0  
　　          1  1  0  0        

 

 

 

• 图的遍历

void dfs(int i)
{
    visited[i] = true;
    for(int j = 1;j <= num[i] ; j++)
    if(!visited[g[i][j]])
    dfs(g[i][j]);
}
int main()
{
    memset(visited,false,sizeof(visited));
    for(int i=1 ; i<=n ;i++)
    
    if(!visited[i])
    dfs(i);
    
}

 

可以看到上面这段遍历整张图的代码中主函数部分，先把图中各点初始化false，每次遍历时先判断两点是否联通将遍历过的点修改为true。

• 欧拉回路
  
  

如果一个图存在一笔画，则一笔画的路径叫做欧拉路，如果最后又回到起点，那这个路径叫做欧拉回路。
定理1：存在欧拉路的条件：图是连通的，有且只有2个奇点。
定理2：存在欧拉回路的条件：图是连通的，有0个奇点。
根据一笔画的两个定理，如果寻找欧拉回路，对任意一个点执行深度优先遍历；找欧拉路，则对一个奇点执行DFS，时间复杂度为O(m+n)，m为边数，n是点数。

样例输入:第一行n，m，有n个点，m条边，以下m行描述每条边连接的两点。
    5 5
    1 2
    2 3
    3 4
    4 5
    5 1
样例输出:欧拉路或欧拉回路
    1 5 4 3 2 1

这种条件在纸上画出大概的一个图就能发现点和线之间的关联。
这也是欧拉回路一个模板

#include<iostream>
using namespace std;
#define maxn 100
int g[maxn][maxn];               //储存矩阵
int du[maxn];                    //记录一个点连了几条边
int circuit[maxn];               //记录欧拉回路
int n,e,circuitpos,i,j,x,y,start;
void find_circuit(int i)         //记录其中一个点的欧拉回路
{
    int j;
    for(j=1;j<=n;j++)
    if(g[i][j]==1)
    {
        g[i][j] = g[j][i] = 0;           //记录两个联通点后把他们的之间路径清空
        find_circuit(j);
    }
    circuit[++circuitpos] = i;
}
int main()
{
    memset(g,0,sizeif(g));
    cin>>n>>e;
    for (int i=1 ;i<=e ;i++)
    {
        cin>>x>>y;
        g[x][y] = g[y][x] =1;
        du[x]++;
        du[y]++;
    }
    start = 1;
    for(i =1 ; i<=n ;i++)
    if(du[i]%2==1)                      //偶数点无法判断此路径是否被记录，因此从奇数点
                                          开始找，找到奇数点后代入函数做记录。
    start = i;
    circuitpos = 0;
    find_circuit(start);
    for(i=1;i<=circuitpos;i++)
    cout<<circuit[i]<<endl;
}

 

• 哈密尔顿环

　　欧拉回路是指不重复地走过所有路径的回路，而哈密尔顿环是指不重复地走过所有的点，并且最后还能回到起点的回路。

#include<iostream>
#include<cstring>
using namespace std;
int start,length,x,n; 
bool visited[101],v1[101];
int ans[101], num[101];
int g[101][101];
void print()
{    int i;
     for (i = 1; i <= length; i++)
         cout << ' ' << ans[i];
     cout << endl;    
}
void dfs(int last,int i)                      //图用数组模拟邻接表存储，访问点i，last表示上次访问的点
{
    visited[i] = true;                        //标记为已经访问过
    v1[i] = true;                             //标记为已在一张图中出现过
    ans[++length] = i;                                     
    for (int j = 1; j <= num[i]; j++)  
　　{ 
　　  if (g[i][j]==x&&g[i][j]!=last)          //回到起点，构成哈密尔顿环
　　        {
　　        ans[++length] = g[i][j];  
　　        print();                          
　　        length--;
　　        break;
　　        } 
     if (!visited[g[i][j]]) dfs(i,g[i][j]);   //遍历与i相关联的所有未访问过的顶点
    }
    length--;
    visited[i] = false;                       
} 
int main()
{
    memset(visited,false,sizeof(visited));
    memset(v1,false,sizeof(v1));
    for (x = 1; x <= n; x++)
       //每一个点都作为起点尝试访问，因为不是从任何一点开始都能找过整个图的
       if (!v1[x])              //如果点x不在之前曾经被访问过的图里。
        {
            length = 0;         
            dfs(x);
        }
    return 0;
}

• 最短路径

 如下图所示，我们把边带有权值的图称为带权图。边的权值可以理解为两点之间的距离。一张图中任意两点间会有不同的路径相连。最短路径就是指连接两点的这些路径中最短的一条。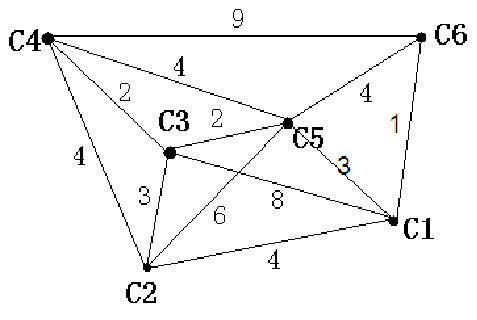

 

 1.弗洛依德l算法 O(N3)
　　简称Floyed(弗洛伊德)算法，是最简单的最短路径算法，可以计算图中任意两点间的最短路径。Floyed的时间复杂度是O (N3)，适用于出现负边权的情况。
算法描述：
       初始化：点u、v如果有边相连，则dis[u][v]=w[u][v]。
　　如果不相连则dis[u][v]=0x7fffffff
For (k = 1; k <= n; k++)
    For (i = 1; i <= n; i++)
     For (j = 1; j <= n; j++)
         If (dis[i][j] >dis[i][k] + dis[k][j])
             dis[i][j] = dis[i][k] + dis[k][j];
        算法结束：dis[i][j]得出的就是从i到j的最短路径。

主体代码是很好理解的，遍历所有点，i,j两点间的距离比i到k，k到j的距离长，就更新i j两点间的距离。

 

最短路径问题
【问题描述】
　　平面上有n个点（n<=100），每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。
　　若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点间的直线距离。现在的
　　任务是找出从一点到另一点之间的最短路径。
【输入格式】
　　输入文件为short.in，共n+m+3行，其中:
　　第一行为整数n。
　　第2行到第n+1行（共n行） ，每行两个整数x和y，描述了一个点的坐标。
　　第n+2行为一个整数m，表示图中连线的个数。
　　此后的m 行，每行描述一条连线，由两个整数i和j组成，表示第i个点和第j个点之间有连线。
　　最后一行：两个整数s和t，分别表示源点和目标点。
【输出格式】
　　输出文件为short.out，仅一行，一个实数（保留两位小数），表示从s到t的最短路径长度

 

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
int a[101][3];
double f[101][101];
int n,i,j,k,x,y,m,s,e;
int main()
{
    cin >> n;
    for (i = 1; i <= n; i++)
        cin >> a[i][1] >> a[i][2];
    cin >> m;
    memset(f,0x7f,sizeof(f));                    //初始化f数组为最大值
    for (i = 1; i <= m; i++)                           //预处理出x、y间距离
    {
      cin >> x >> y;
      f[y][x] = f[x][y] = sqrt(pow(double(a[x][1]-a[y][1]),2)+pow(double(a[x][2]-a[y][2]),2));
                      //求(x1,y1),(x2,y2)距离 
    }
    cin >> s >> e;
    for (k = 1; k <= n; k++)                     //floyed 最短路算法
       for (i = 1; i <= n; i++)
          for (j = 1; j <= n; j++)
             if ((i != j) && (i != k) && (j != k) && (f[i][k]+f[k][j] < f[i][j]))
                 f[i][j] = f[i][k] + f[k][j];
    printf("%.2lf\n",f[s][e]);
    return 0;
}

2.Dijkstra算法O (N2)
用来计算从一个点到其他所有点的最短路径的算法，是一种单源最短路径算法。也就是说，只能计算起点只有一个的情况。
Dijkstra的时间复杂度是O (N2)，它不能处理存在负边权的情况。dijkstra算法优点在于时间复杂度比弗洛伊德低一个量级，但是不能处理负权值。
算法描述：
       设起点为s，dis[v]表示从s到v的最短路径，pre[v]为v的前驱节点，用来输出路径。
       a)初始化：dis[v]=∞(v≠s); dis[s]=0; pre[s]=0;
       b)For (i = 1; i <= n ; i++)
            1.在没有被访问过的点中找一个顶点u使得dis[u]是最小的。
            2.u标记为已确定最短路径
            3.For 与u相连的每个未确定最短路径的顶点v
              if  (dis[u]+w[u][v] < dis[v])
               {
                  dis[v] = dis[u] + w[u][v];
                  pre[v] = u;
               }
        c)算法结束：dis[v]为s到v的最短距离；pre[v]为v的前驱节点，用来输出路径。

    从起点到一个点的最短路径一定会经过至少一个“中转点”（例如下图1到5的最短路径，中转点是2。特殊地，我们认为起点1也是一个“中转点”）。显而易见，如果我们想求出起点到一个点的最短路径，那我们必然要先求出中转点的最短路径（例如我们必须先求出点2 的最短路径后，才能求出从起点到5的最短路径）。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int a[101][3];
double c[101];
bool b[101];
double f[101][101];
int n,i,j,k,x,y,m,s,e;
double minl;
double maxx = 1e30;
int main()
{
    cin >> n;
    for (i = 1; i <= n; i++)
      cin >> a[i][1] >> a[i][2];
    for (i = 1; i <= n; i++)
      for(j = 1; j <= n; j++)
        f[i][j] = maxx;                         //f数组初始化最大值
    cin >> m;
    for (i = 1; i <= m; i++)                    //预处理x.y间距离f[x][y]
    {
        cin >> x >> y;
        f[x][y] = f[y][x] = sqrt(pow(double(a[x][1]-a[y][1]),2)+pow(double(a[x][2]-a[y][2]),2));
    }
   cin >> s >> e;
    for (i = 1; i <= n; i++) 
      c[i] = f[s][i];
    memset(b,false,sizeof(b));      //dijkstra 最短路
    b[s] = true;
    c[s] = 0; 
    for (i = 1; i <= n-1; i++)
    {
        minl = maxx;
        k = 0;
        for (j = 1; j <= n; j++)     //查找可以更新的点
           if ((! b[j]) && (c[j] < minl))
            {
                minl = c[j];
                k = j;
            }
        if (k == 0) break;
        b[k] = true;
        for (j = 1; j <= n; j++)
           if (c[k] + f[k][j] < c[j]) 
             c[j] = c[k] + f[k][j];
    }    
   printf("%.2lf\n",c[e]);
   return 0;
}

 

转载于:https://www.cnblogs.com/sylover/p/10820630.html