图论基础算法
图的存储与遍历
邻接表
经历了链表的学习,邻接表的存法就不会让人发难了。
我们仍然使用idx表示位置,ne数组表示当前位置的下一个位置,e数组表示当前位置的值,不同的是,我们用h数组来存储每一个点作为头结点的链表,每当有一个边时,我们便把该边终点的位置存入前一个点的链表。具体实现在遍历中体现。
该方法适用于点数较多的情况的存储(即稀疏图)
邻接矩阵
邻接矩阵更容易理解,即用一个二维数组来表示两点间边的距离,不存在的话可以用特殊值来表示,即g[a][b]表示a、b两点间边的距离。具体实现在最短路算法中体现。
邻接矩阵适用于存储边数较多的情况。(即稠密图)
图的深度优先遍历
即在图上用dfs,很好理解,那就直接上例题。
AcWing846
有同学会问,这不是树的问题吗?
树就是特殊的图,也是可以用邻接表来存的,我们就来看下这题。
由于是无向图,我们可以任选一个结点开始深搜,搜到一个节点时,就递归求出与它相连的几个连通块中点的数量,然后取最大值更新答案(说白了,就是爆搜),然而,当我们搜到一个点,怎么求它的来处的连通块的点数呢?如图:
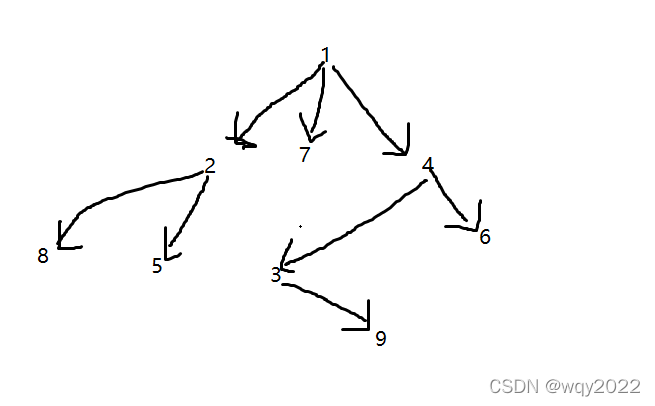
当我们从1搜到4这个点,我们可以递归求出4指向的两个连通块的点数,但是1、2、5、7、8这个连通块好像没法求,因为它已经被我们标记过,不会再搜回去了,但是它的点数其实就是总点数减去1(当前点),再减去4指向的两个连通块的点数,这样我们就可以求出最终结果了。
代码:
#include<iostream>
using namespace std;
int n;
const int N=1e5+10,M=N*2;
int h[N],ne[M],e[M],idx=1;//h的大小是N是因为点数不会超过N,而ne,e数组的大小是二倍N是因为边数不会超过2*N
bool vis[N];//记录某个点有没有搜过
int ans=N;//把ans初始化为一个较大的值
void add(int a,int b){//加一条从a指向b的边,相当于在a的链表中头插一个b的位置
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dfs(int x){
vis[x]=1;//标记当前点为已搜过
int sum=1,res=0;//sum记录以当前点为根节点的子树的点数总和
//res记录当前点指向的连通块的最大点数
for(int i=h[x];i;i=ne[i]){
int j=e[i];
int s=0;
if(!vis[j]) s=dfs(j);//s是连通块的点数
res=max(res,s);//更新res
sum+=s;//更新sum
}
res=max(res,n-sum);//用那个搜不到的连通块“尝试”更新res
ans=min(ans,res);//更新ans
return sum;//返回以当前点为根节点的子树的点数总和
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;i++){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);//无向图,加两条边
add(b,a);
}
dfs(1);
printf("%d",ans);
return 0;
}
图的广度优先遍历
在bfs中我们经常求最短路问题,在图中我们也是可以用bfs求解边权相等和边权只有0、1的最短路(双端队列广搜)问题的,这个也比较简单。
直接上例题:
AcWing847
简单bfs代码:
//这里也可以只用一个d数组而不用vis数组,把d数组全部初始化为-1
#include<iostream>
using namespace std;
int n,m;
const int N=1e5+10;
bool vis[N];//记录某点有没有搜过
int e[N],ne[N],h[N],idx=1,d[N];//d数组表示各点到1的距离
int q[N],hh=0,tt=0;//这里用数组模拟队列
void add(int a,int b){//老样子
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs(){
q[0]=1;
vis[1]=true;
while(hh<=tt){
auto t=q[hh++];
for(int i=h[t];i;i=ne[i]){
int j=e[i];
if(!vis[j]){
q[++tt]=j;
d[j]=d[t]+1;
vis[j]=1;
}
if(j==n) return d[n];
}
}
return -1;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
}
printf("%d",bfs());
return 0;
}
拓扑序列
拓扑序列定义参考这道题:AcWing848
比如一个简单的图:
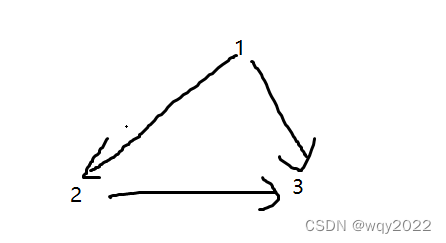
1->2->3就是一个拓扑序列,因为它满足1在2前面,2在3前面,1在3前面,而1->3->2就显然不是拓扑序列了,因为2->3有一条边,2应该在3前面
我们容易得到,只有有向图才有拓扑序列,有向无环图(又叫拓扑图)一定存在拓扑序列。
继续思考,我们发现每个点都可能有指向别的点的边和被指的边,我们成为入度和出度,比如,有三条边指向4,则4的入度就是3,4有5条边指出,4的出度就是5。我们用一个队列存储答案,遍历所有点,当一个点的入度是0时,把它加入队列中,因为没有数会在它前面了。让队列中第一个点出队,顺便把这个点指向的数的入度都减1,因为这些数必须在这个点后面的条件都满足了,再把入度为0的点入队,直到队列为空,如果所有点都已入队,则存在拓扑序列,反之不存在。
代码:
#include<iostream>
using namespace std;
int n,m;
const int N=1e5+10;
int h[N],ne[N],e[N],idx=1,in[N];
int hh=0,tt=-1,q[N];//这里用数组模拟队列,因为我们让队列里的元素出队时只是让hh++,并不会真的删除,这样我们就可以先判断是否满足有拓扑序列再输出了
void add(int a,int b){//老样子
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool hastop(){
for(int i=1;i<=n;i++){
if(!in[i]){//入度为0的点入队
q[++tt]=i;
}
}
while(hh<=tt){//队列不空
auto t=q[hh++];//队头出队
for(int i=h[t];i;i=ne[i]){//遍历所有出边
int j=e[i];
in[j]--;//指向点的入度--
if(in[j]==0) q[++tt]=j;//入度为0的入队
}
}
return tt==n-1;//tt为n-1时说明所有点都已入队(0~n-1,n个点)
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);//a指向b的边
in[b]++;//b的入度++
}
if(hastop()){
for(int i=0;i<n;i++){
printf("%d ",q[i]);//打印拓扑序
}
}
else{
printf("-1");
}
return 0;
}
关于拓扑序列,还有很重要的两条性质:
- 若遍历的层数(深度)与点数相同,则说明拓扑序是稳定的(即存在唯一拓扑序)
- 如果图中存在环,则一定无法遍历所有点
最短路算法
朴素dijkstra算法
时间复杂度:O(n^2),n为点数,m为边数
给定我们一个图,求1号点到n号点的最短距离
dijkstra算法流程:
首先将各个点之间的距离初始化为INF(一般为0x3f3f3f3f),把各个点到起点的距离设为不确定,然后将起点到起点的位置设为0,然后从所有到1号点最短距离为不确定的点中选出距离最近的那一个,用它到起点的距离来更新它的所有出边能到达的点的距离起点的距离,然后把该点改为已确定到1号点的最短距离,如此循环n次,就能求出1号点到n号点的最短距离。
适用范围:求单源最短路,且不能包括负权边
至于这样为什么是对的,感兴趣的同学可以自行百度,这里侧重应用。
我们来模拟一个样例,来加深理解:
求1到3的最短距离,红色数字表示未确定最短的到起点的距离,绿色表示已经确定的到起点的最短距离

经过这样一个样例的模拟,我们好像感觉到这个算法是对的,但是具体证明还是不太会,有兴趣的可以参考《算法导论》P383,不过算法竞赛中一般不会用到证明。
例题:AcWing849
代码:
#include<iostream>
#include<cstring>
using namespace std;
int n,m;
const int N=510;
int g[N][N];
bool st[N];
int ans[N];
int dijkstra(){
memset(ans,0x3f,sizeof ans);
ans[1]=0;//把起点距离起点距离设为0
for(int i=1;i<n;i++){//循环n-1次,因为最后只会剩一个终点,不会再更新终点了
int t=-1;//随便一个负数或0
for(int j=1;j<=n;j++){//找到未确定到起点最短距离中最短的一个,下标记为t
if(!st[j]&&(t==-1||ans[t]>ans[j])){
t=j;
}
}
st[t]=1;//标记为已经确定
for(int j=1;j<=n;j++){//用这个点更新别的点
ans[j]=min(ans[j],ans[t]+g[t][j]);
}
}
return ans[n]==0x3f3f3f3f?-1:ans[n];//ans[n]为正无穷即表示无法到达n点
}
int main(){
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof g);
for(int i=0;i<m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b]=min(g[a][b],c);//由于存在重边和自环,我们只存一条最短的边,自环存入也不会影响最终结果,因为边权均为正数
}
printf("%d",dijkstra());
return 0;
}
堆优化dijkstra算法
时间复杂度:O(m*log n),m为边数,n为点数
上面的算法很简单,但是当我们遇到点数较多的情况,上述算法就无法很好地完成任务了,此时我们需要用邻接表来存储图,而找到最小值的过程我们可以使用单调队列优化。
手写堆
堆有小根堆和大根堆之分,其实就是一个二叉树,数的根节点是整棵树的最小值(小根堆)或最大值(大根堆),其实这个玩意很简单,就整一道例题吧。
AcWing838
代码实现:
#include<iostream>
using namespace std;
int n,m;
const int N=1e5+10;
int cnt;
int heap[N];
void down(int x){
//找到此节点和它的两个儿子中的最小的那个
int t=x;
if(x*2<=cnt&&heap[x*2]<heap[t]) t=x*2;
if(x*2+1<=cnt&&heap[x*2+1]<heap[t]) t=x*2+1;
if(t!=x){//如果此节点不是最小,则把此节点和最小的那个交换
swap(heap[t],heap[x]);
down(t);//递归处理
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",heap+i);
}
cnt=n;//cnt记录堆的大小
for(int i=n/2;i;i--) down(i);//n/2就是最后一个结点的父亲,从它开始down
while(m--){
printf("%d ",heap[1]);
heap[1]=heap[cnt--];//把堆顶改为堆中最后一个数,同时cnt--
down(1);//让堆顶回到应该待的位置
}
return 0;
}
(千万不要随便花里胡哨,我刚开始把x*2写成x<<1,把2*x+1写成x<<1|1结果就segmentation fault了,这还没到线段错误树线段树呢啊)
类似地,我们可以写一个up操作,感兴趣的可以自己尝试。
代码
本人太懒了,这里就不手写堆了。。。
此题链接:AcWing850
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=150010;
int n,m;
int h[N],e[N],ne[N],w[N],idx=1,dist[N];
bool st[N];//判断当前点是否已经确定为最短距离
typedef pair<int,int> PII;
void add(int a,int b,int c){
e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
int dijkstra(){
memset(dist,0x3f,sizeof dist);
priority_queue<PII,vector<PII>,greater<PII> > heap;
heap.push({0,1});
dist[1]=0;
while(heap.size()){//遍历大部分的边
auto t=heap.top();//取出堆顶元素
heap.pop();
int x=t.second;
if(st[x]) continue;//如果这个点已经确定过了并且也用它更新过出边了,就没必要继续了,虽然继续也是对的(不会再更新),不过可能会超时
st[x]=true;
for(int i=h[x];i;i=ne[i]){//遍历所有出边
int j=e[i];
if(dist[j]>dist[x]+w[i]){//一旦此结点距离被更新,就加入优先队列中
dist[j]=dist[x]+w[i];
heap.push({dist[j],j});//堆插入的时间复杂度为O(log n);
}
}
}
return dist[n]==0x3f3f3f3f?-1:dist[n];
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);//自环和重边都不会影响结果,因为最终结果还是被最短的那个更新的
}
printf("%d",dijkstra());
return 0;
}
bellman-ford算法
时间复杂度O(n*m)
bellman-ford算法可以用来求有边数限制的最短路问题,流程很简单:假设边数限制为k,那就循环k次,每一次都枚举每条边并更新,最终就能得到每个点到起点不超过k条边的最短距离,这里也不具体讲证明了,感兴趣的参考《算法导论》P379或自行百度。
优势:即求出有边数限制的最短路,写着简单,不受负环和负权边影响
其它用途:判断负环,循环n次(n为点数),如果第n次距离仍有更新,说明存在负环,但时间复杂度较高,一般会用spfa来判断。
例题:AcWing853
代码实现:
#include<iostream>
#include<cstring>
using namespace std;
int n,m,k;
const int N=510,M=1e4+10;
int dist[N],backup[N];
struct line{
int a,b,c;
}l[M];
void bellman_ford(){
dist[1]=0;
for(int i=0;i<k;i++){
memcpy(backup,dist,sizeof dist);//这里要备份,,防止串联
for(int i=0;i<m;i++){
int a=l[i].a,b=l[i].b,c=l[i].c;
dist[b]=min(dist[b],backup[a]+c);//松弛操作
}
}
}
int main(){
memset(dist,0x3f,sizeof dist);
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
l[i]={a,b,c};
}
bellman_ford();
if(dist[n]>0x3f3f3f3f/2) puts("impossible");//有负权路,因此dist[n]可能会变小一点
else printf("%d",dist[n]);
return 0;
}
串联举例:

求1到3且边数限制为1的最短路,本来正确答案应该是3,但是1更新了2之后,2会用更新后的数据更新3,由此引发了错误。所以应该保证这一层所用的都是上一层未修改过的数据。
spfa算法
spfa算法可以看成是对bellman-ford算法的一个优化,时间复杂度一般是O(m),最坏O(n*m)。
缺点:不能处理包括负环的最短路问题。
优点:较高效地处理包括负权边的最短路问题,也能氵一氵只有正权边的最短路问题。
我们知道,bellman-ford算法中我们用d[b]=max(d[b],d[a]+w);来更新d数组,其实,如果d[a]没有改变的话d[b]也不会变,因此我们用队列来优化bellman-ford算法,首先让起点入队,然后更新它的出边,如果它的出边到的点被更新了,就把它加入队列。
代码实现:
//经过前面算法的洗礼,这个也没什么好解释的了。。。
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
int n,m;
const int N=1e5+10;
int h[N],e[N],ne[N],idx=1,w[N];
int dist[N];
bool st[N];//判断每个数是否在队列中,以此取消无意义的重复入队
queue<int> q;//懒人专用(bushi
void add(int a,int b,int c){
e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
void spfa(){
memset(dist,0x3f,sizeof dist);
dist[1]=0;
q.push(1);
st[1]=1;
while(q.size()){
auto t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
if(!st[j]){
q.push(j);
st[j]=1;
}
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
spfa();
if(dist[n]==0x3f3f3f3f) puts("impossible");
else printf("%d",dist[n]);
return 0;
}
floyd算法
时间复杂度:O(n^3)
特点:可以求多源最短路。
缺点:也不能处理负权回路
floyd基于动态规划思想,我们用邻接矩阵存储图,用状态转移方程计算每两个点之间的最短距离
例题:AcWing854
代码实现:
#include<iostream>
#include<cstring>
using namespace std;
int n,m,k;
const int N=210;
int dp[N][N];
void floyd(){
for(int k=1;k<=n;k++){//k必须在最外层
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);//从i到j最短距离、从i到k最短距离与从k到j最短距离之和两者取最小值
}
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&k);
memset(dp,0x3f,sizeof dp);
for(int i=1;i<=n;i++){
dp[i][i]=0;//自己到自己距离初始化为0
}
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
dp[a][b]=min(dp[a][b],c);//保留一个最小的
}
floyd();
while(k--){
int a,b;
scanf("%d%d",&a,&b);
int t=dp[a][b];
if(t>0x3f3f3f3f/2) puts("impossible");
else printf("%d\n",t);
}
return 0;
}
强烈推荐一道题,做完后让你对此算法有新的认识:洛谷P1119
spfa判断负环
前面我们提到过:spfa是能用来判断负环的。
基本思路:用一个cnt数组记录以某个点结尾的最短路经过的边的个数,如果有一个cnt大于等于n(点数),说明存在环,而只有距离被更新时cnt才会更新,因此一定是负环。
例题:AcWing852
代码:
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
int n,m;
const int N=1e5+10;
int h[N],e[N],ne[N],idx=1,w[N];
int dist[N],cnt[N];
bool st[N];
queue<int> q;
void add(int a,int b,int c){
e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
bool spfa(){
//memset(dist,0x3f,sizeof dist);
//dist[1]=0;
//这题也可以不初始化距离,只要有负环,最终都会有一个cnt大于等于n
for(int i=1;i<=n;i++){//因为可能有起点不能走到负环的情况,因此我们需要把所有点加入队列
q.push(i);
st[i]=1;
}
while(q.size()){
auto t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;//以j结尾的边数为以t结尾的边数+1
if(cnt[j]>=n) return true;
if(!st[j]){
q.push(j);
st[j]=1;
}
}
}
}
return false;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
if(spfa()) puts("Yes");
else puts("No");
return 0;
}
最小生成树
最小生成树:一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
prim算法
prim算法流程:(这里同样不讲解证明),首先随便选取一个结点,把除此节点外的其它结点到连通块的距离初始化维INF(正无穷),然后循环n(点数)次,每次找出不在连通块中距离连通块最近的点,将它加入连通块,并用它更新别的点到连通块的距离,过程中不断累加res,即可得到答案。
例题:AcWing860
朴素prim算法
时间复杂度O(n^2),n为点数
代码实现:
//res为最小生成树所有边的权值之和
#include<iostream>
#include<cstring>
using namespace std;
int n,m;
const int N=510;
int g[N][N];//稠密图用邻接矩阵
bool st[N];//判断结点是否在连通块中
int dist[N];//各点到连通块距离
int prim(){
int res=0;//结果
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=1;i<=n;i++){
int t=-1;
for(int j=1;j<=n;j++){//找出不在连通块中距离最小的一个
if(!st[j]&&(t==-1||dist[j]<dist[t])){
t=j;
}
}
if(dist[t]==0x3f3f3f3f) return 0x3f3f3f3f;//如果最近的距离依然是正无穷,说明没有最小生成树
st[t]=1;//加入连通块
res+=dist[t];//加上答案,一定要先加上,再更新,否则负的自环可能会让你WA
for(int i=1;i<=n;i++){//用它更新别的点到连通块的距离
dist[i]=min(dist[i],g[i][t]);
}
}
return res;//返回答案
}
int main(){
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof g);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b]=g[b][a]=min(g[a][b],c);//重边只保留最短的一条
}
int t=prim();
if(t==0x3f3f3f3f) puts("impossible");
else printf("%d\n",t);
return 0;
}
堆优化prim算法
时间复杂度:O(m*log n),m为边数,n为点数
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
int n,m;
typedef pair<int,int> PII;
const int N=510,M=2e5+10;
int e[M],ne[M],idx=1,h[N],w[M];
bool st[N];
int dist[N];
priority_queue<PII,vector<PII>,greater<PII>> q;
void add(int a,int b,int c){
e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
int prim(){
int res=0;
memset(dist,0x3f,sizeof dist);
dist[1]=0;
q.push({0,1});
while(q.size()){
auto t=q.top();
q.pop();
int x=t.second;
if(st[x]) continue;//如果已经确定过,说明该点已经更新过出边,直接跳过后面的
st[x]=1;
res+=dist[x];
for(int i=h[x];i;i=ne[i]){
int j=e[i];
if(dist[j]>w[i]){
dist[j]=w[i];
q.push({w[i],j});
}
}
}
for(int i=1;i<=n;i++){//因为在上面我们找的是被更新的点中离连通块最近的,所以不会遇到INF,我们就判断是否所有点都在连通块中
if(!st[i]){
return 0x3f3f3f3f;
}
}
return res;
}
int main(){
scanf("%d%d",&n,&m);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
int t=prim();
if(t==0x3f3f3f3f) puts("impossible");
else printf("%d\n",t);
return 0;
}
kruskal算法
时间复杂度O(m*log m),m为边数
算法流程:首先,将每个点分别赋予一个集合,将所有边按照从小到大的顺序排序,然后,枚举每条边,如果这条边连接的两个点不在同一集合中,则res加上这条边,并把这两个点联通,最后判断加入集合中的点数是否为n-1(n为总点数)即可
例题:AcWing859
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
const int M=2e5+10,N=1e5+10;
struct edge{//存储边
int a,b,w;
bool operator<(edge & s)const{//重载<号,写成cmp函数也可
return w<s.w;
}
}l[M];
int p[N];//并查集
int find(int x){//找祖宗
if(p[x]!=x) p[x]=find(p[x]);//路径压缩
return p[x];
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
l[i]={a,b,c};
}
sort(l+1,l+m+1);
for(int i=1;i<=n;i++) p[i]=i;//初始化每个集合
int res=0,cnt=0;
for(int i=1;i<=m;i++){//从小到大枚举每条边
int a=l[i].a,b=l[i].b,w=l[i].w;
a=find(a),b=find(b);//找到a,b的祖宗
if(a!=b){//祖宗不同
p[a]=b;//连接两个集合
res+=w;//边权之和加上w
cnt++;//点数++
}
}
if(cnt==n-1)printf("%d",res);//因为刚开始也有一个点,因此判断与n-1是否相等
else puts("impossible");
return 0;
}
二分图
二分图:二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
二分图,简单来说就是我们可以把图中点分为两个集合,且集合内部没有边。
简单的判断:当且仅当一个图能被二染色,说明此图是二分图,也就是图中不含奇数环。
可以自行画图理解。
染色法
时间复杂度O(m+n),m为边数,n为点数
很容易,如果一个点被染成2中不同颜色,则一定存在奇数环,该图就不是二分图。
例题:AcWing860
代码实现:
#include<iostream>
using namespace std;
int n,m;
const int N=1e5+10,M=N*2;
int e[M],h[N],ne[M],idx=1,color[N];//color存储每个点的染色情况,为0表示未染色,为1表示染上第一种颜色,为2表示染上第二种颜色
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool dfs(int x,int col){
color[x]=col;//染色
for(int i=h[x];i;i=ne[i]){
int j=e[i];
if(!color[j]){//如果没染过色
if(!dfs(j,3-col)) return false;//如果递归的过程中发生矛盾,返回false,3-color表示如果当前color为1,下一个染为2,如果当前color为2,下一个染为1
}
else if(color[j]==col) return false;//如果一条边连着的两点颜色相同,则返回false
}
return true;//无矛盾
}
int main(){
scanf("%d%d",&n,&m);
while(m--){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
add(b,a);
}
bool flag=true;//初始化为true
for(int i=1;i<=n;i++){
if(!color[i]){//如果此点未染色
if(!dfs(i,1)){//一旦发生矛盾,改为false,跳出循环
flag=false;
break;
}
}
}
if(flag) puts("Yes");
else puts("No");
return 0;
}
匈牙利算法
时间复杂度:O(mn),不过一般会快很多,m是边数,n是点数
用途:求二分图的最大匹配数
相关概念见例题:AcWing861
y总的奇妙比喻:左边的集合是男生,右边的集合是女生,男女相互匹配,最大匹配数就是在没有人脚踏两条船情况下男女配对成功中边数最多的一次的边数(注意:只有两者之间有连边的才能匹配,y总比喻为有好感)。
我们匹配的流程大致是怎样的呢?
我们枚举所有男生,看看他指向的女生是否已经有配对的人了,若没有,则配对,若有,则看一下该女生配对的男生能不能换一个女生,如果能就换,然后该女生再与此男生配对,如果遍历所有指向的女生也没能配对,就配对失败了,如果成功了,就res++。
代码实现:
#include<iostream>
#include<cstring>
using namespace std;
const int N=510,M=1e5+10;
int n1,n2,m;
int e[M],ne[M],h[N],idx=1,match[N];//match记录每个女生配对的男生
bool st[N];//记录考虑过哪些女生
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool find(int x){
for(int i=h[x];i;i=ne[i]){
int j=e[i];
if(!st[j]){
st[j]=true;
if(match[j]==0||find(match[j])){//如果该女生还未配对或者配对的男生能找到新的女生,由于该女生已经被标记为考虑过,该女生不会被配对男生再次考虑
match[j]=x;//配对
return true;//返回true
}
}
}
return false;
}
int main(){
scanf("%d%d%d",&n1,&n2,&m);
for(int i=0;i<m;i++){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);//因为我们只枚举所有男生,因此这里赋成单向边
}
int res=0;
for(int i=1;i<=n1;i++){
memset(st,0,sizeof st);//清空st数组
if(find(i)) res++;
}
printf("%d\n",res);
return 0;
}

























 2086
2086

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










