要点一、两线相交与对顶角、邻补角
1.对顶角
(1)定义:如果两个角有一个公共顶点, 而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫对顶角.
(2)性质:对顶角相等.
2.邻补角(1)定义:有一条公共边,而且另一边互为反向延长线的两个角叫做邻补角.(2)性质:邻补角互补.
3.垂线(1)定义:当两条直线相交所得的四个角中,有一个角是直角时,就说这两条直线是互相垂直的,它们的交点叫做垂足.垂直用符号“⊥”来表示.要点诠释: ①过一点有且只有一条直线与已知直线垂直.
②连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.(2)点到直线的距离定义:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
要点二、 三线相交与同位角、内错角和同旁角
1. “三线八角”模型
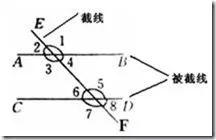
如图,直线AB、CD与直线EF相交(或者说两条直线AB、CD被第三条直线EF所截),构成八个角,简称为“三线八角”,如图1.
要点诠释:
⑴两条直线AB,CD与同一条直线EF相交.
⑵“三线八角”中的每个角是由截线与一条被截线相交而成.
2. 同位角、内错角、同旁内角的定义
在“三线八角”中,如上图1,
(1)同位角:像∠1与∠5,这两个角分别在直线AB、CD的同一方,并且都在直线EF的同侧,具有这种位置关系的一对角叫做同位角.
(2)内错角:像∠3与∠5,这两个角都在直线AB、CD之间,并且在直线EF的两侧,像这样的一对角叫做内错角.
(3)同旁内角:像∠3和∠6都在直线AB、CD之间,并且在直线EF的同一旁,像这样的一对角叫做同旁内角.
要点诠释:
(1)“三线八角”是指上面四个角中的一个角与下面四个角中的一个角之间的关系,显然是没有公共顶点的两个角.
(2)“三线八角”中共有4对同位角,2对内错角,2对同旁内角.
3、同位角、内错角、同旁内角位

置特征及形状特征
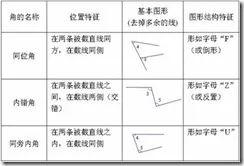
要点诠释:巧妙识别三线八角的两种方法:
(1)巧记口诀来识别: 一看三线,二找截线,三查位置来分辨.
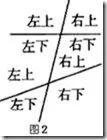
(2)借助方位来识别
根据这三种角的位置关系,我们可以在图形中标出方位,判断时依方位来识别,如图2.
要点三、平行线及平行公理
1.平行线的定义
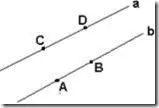
在同一平面内,不相交的两条直线叫做平行线. 两直线平行,用符号“∥”表示. 如下图,两条直线互相平行,记作AB∥CD或a∥b.
要点诠释:
(1)同一平面内,两条直线的位置关系:相交和平行.
(2)互相重合的直线通常看作一条直线,两条线段或射线平行是指它们所在的直线平行.
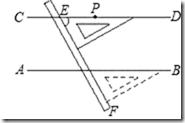
2.平行线的画法
用直尺和三角板作平行线的步骤:
①落:用三角板的一条斜边与已知直线重合.
②靠:用直尺紧靠三角板一条直角边.
③推:沿着直尺平移三角板,使与已知直线重合的斜边通过已知点.
④画:沿着这条斜边画一条直线,所画直线与已知直线平行.
3.平行线的性质
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
要点诠释:
(1)“同位角相等、内错角相等”、“同旁内角互补”都是平行线的性质的一部分内容,切不可忽视前提 “两直线平行”.
(2)从角的关系得到两直线平行,是平行线的判定;从平行线得到角相等或互补关系,是平行线的性质.
4. 两条平行线间的距离
同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度,叫做这两条平行线
间的距离.
要点诠释:
(1)求两条平行线的距离的方法是在一条直线上任找一点,向另一条直线作垂线,垂线段的长度就是两条平行线的距离.
(2) 两条平行线的位置确定后,它们的距离就是个定值,不随垂线段的位置的改变而改变,即两条平行线之间的距离处处相等.
转载请注明:轩爸辅导 » 数学七下,第一章,平行线的概念和性质,知识要点
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








