新小学六年级下册数学试题及答案(1)
一.填空题(共11 小题,满分18 分)
1.( 2 分) 时= 15 分0.68 吨= 千克.
2.( 4 分)观察如图,将阴影部分与整个图形面积的关系分别用最简分数、最简整数比、
百分数和除法算式表示:
= := %= ÷24
3.( 1 分)小明做了20 道口算题,错了1 道,他这次口算的准确率是.
4.( 2 分)一辆汽车行千米用汽油升.行1 千米用汽油升, 1 升汽油可以行
千米.
5.( 2 分)求半圆的周长和面积
(1)周长= dm.(结果用小数表示)
(2)面积= dm2.(结果用小数表示)
6.(2 分)比25m 长m 是m,18dm3 的是cm3, kg 的是18kg.
7.( 1 分)有一个等腰三角形,它的两个角的度数比是1:2,这个三角形按角分类可能是
什么三角形?
8.( 1 分)学校新买了2 个篮球和6 个足球,正好用去了360 元.足球的单价是篮球单价
的.篮球的单价是元.足球的单价是元.
9.( 1 分)比40 米多25%是米. 40 米比米少20%.
10.( 1 分)一根绳子长10 米,用去25%,剩米.
11.( 1 分)在A 地植树1000 棵, B 地植树1250 棵,甲、乙、丙每天分别能植树28、32、
30 棵,甲在A 地,乙在B 地,丙在A 与B 两地之间来回帮忙,同时开始,同时结束,丙
在A 地植树棵.
二.判断题(共5 小题,满分5 分,每小题1 分)
12.(1 分)一件原价200 元的商品, 先提价20%,再八折出售, 仍卖200 元. .(判
断对错)
13.(1 分) 一个圆的半径扩大到原来的2 倍,它的面积也扩大到原来的2 倍. (判
断对错)
14.( 1 分) 1 米与1 厘米的比是1:1. (判断对错)
15.( 1 分)边长为2 厘米的正方形,周长和面积相等. .(判断对错)
16.( 1 分) 和的大小相等它们的分数单位也相等. (判断对错)
三.选择题(共5 小题,满分10 分,每小题2 分)
17.( 2 分)在一个钟面上,时针长2 厘米,分针长3 厘米,从8:00 到10:00,分针扫过
的面积是( )
A .28.26cm2 B.37.68cm2 C. 56.52cm2
18.( 2 分)某小学组织学生春游,学校买了182 瓶汽水送给每个学生,如果5 个空瓶可以
换得一瓶汽水,这些汽水瓶最多可以换得( )瓶汽水.
A .36 B.38 C.15 D.45
19.(2 分)养鸡场养公鸡400 只,养的母鸡比公鸡的只数多.母鸡比公鸡多( )只.
A .400×( 1﹣ ) B.400× C.400×( 1+ )
20.( 2 分)下面图形不一定是轴对称图形的是( )
A .圆B.三角形C.长方形D.正方形
21.(2 分)100 元钱买了100 只鸟, 大鸟3 元钱一只, 小鸟1 元钱3 只. 大鸟买了( )
只.
A .30 B.25 C.75 D.10
四.计算题(共3 小题,满分27 分)
22.( 6 分)直接写出下面各题的计算结果.
(1) = (2) = (3) 15× = (4)9÷ = ( 5) ÷15×
=
(6) + = (7) × 0.6= (8) ÷8= (9) ÷ = ( 10 ) ×
30+ ×30=
23.( 9 分)解方程.
3x﹣8=16 x+0.7= 3.6 2.4× 5﹣2x=6
x+2.8x= 4.56 (100﹣ x)÷ 5=4 5( x﹣ 1.8)= 18
24.( 12 分)能简算的要简算.
2.4× 7.6+76× 0.66+7.6
﹣[ ﹣( + ) ]
999×99
﹣ +
﹣ + ﹣ + ﹣ + ﹣
五.解答题(共2 小题,满分8 分,每小题4 分)
25.( 4 分)
直接得数.
1﹣55%=
1+63%= 2.5× 40%=
8×1.25%= 4.2÷60= ×320%=
50%+ = ﹣ 25%=
26.( 4 分)如图,三角形ABC 的面积为15 平方米, AF=FD,CD= BC,求阴影部分的
面积.
六.应用题(共8 小题,满分32 分,每小题4 分)
27.( 4 分)某电器商场去年销售了1800 台电脑,今年的销售量比去年增加了,今年销
售了多少台?
28.( 4 分)如图是两个互相啮合的齿轮,它们在同时间内转动时,大齿轮和小齿轮转过的
总齿数是相同的,大齿轮有36 个齿,小齿轮有20 个齿,如果小齿轮每分钟转90 圈,大
齿轮每分钟转多少圈?
29.( 4 分)一个圆形花坛,内直径是4 米,如果在外面铺一层1 米宽的石子路,石子路的
面积是多少平方米?
30.( 4 分)一种玉米种子经发芽实验,发芽率达96%,为了保证发芽480 粒,至少应准备
多少粒玉米种子?
31.(4 分)一杯盐水的含盐率是25%,如果加入20 克水, 那么盐水的含盐率变为15%.这
杯盐水原来含盐多少克?
32.( 4 分)修一段公路,甲队单独修20 天可以完成,乙队单独修30 天可以完成,现在两
队合修,中途甲队休息2.5 天,乙队休息若干天,这样一共14 天完成.问:乙队休息了
几天?
33.( 4 分)在甲、乙两地间的公路上,规定从甲地向乙地方向行驶的车辆的速度为每小时
50 千米,从乙地向甲地方向行驶的车辆的速度为每小时60 千米.今有A、B 两辆车,同
时从甲、乙两地相向出发,在两地间往返行驶.在A 车到达乙地向甲地返回途中因故停
车,停车地点距乙地30 千米,在此处两车第二次相遇,这样两车相遇时间比原定第二次
相遇时间晚了1 小时12 分.那么,甲、乙两地之间的距离是多少千米?
34.( 4 分)一根竹竿,第一次截去全长的,第二次截去的比第一次多96 厘米,这时剩
下的长度占这根竹竿的.这根竹竿长多少厘米?
参考答案与试题解析
一.填空题(共11 小题,满分18 分)
1. 【解答】解:因为1 小时= 60 分, 1 吨= 1000 千克,
所以15 分= 15× = = 0.25 小时,
0.68 吨= 0.68×1000=680 千克;
故答案为:0.25、680.
2. 【解答】解:=3:8=37.5%=9÷24.
故答案为:,3,8, 37.5,9.
3. 【解答】解:( 20﹣1)÷ 20× 100%
=19÷20× 100%
=95%.
答:他这次口算的正确率是95%.
故答案为:95%.
4. 【解答】解:÷ = (升)
÷ =12 (千米)
答:行1 千米用汽油升, 1 升汽油可以行12 千米.
故答案为:,12 .
5. 【解答】解:( 1) 3.14×4+4×2
= 12.56+8
= 20.56(分米)
答:周长是20.56 分米.
(2) 3.14×42÷2
= 3.14×16÷2
= 25.12(平方分米)
答:面积是50.24 平方分米.
故答案为:20.56;25.12.
6. 【解答】解:25+ =25 (m)
18× =15(dm3)
15dm3=15000(cm3)
18÷ =24( kg)
答:比25m 长m 是25 m,18dm3 的是15000cm3,24kg 的是18kg.
故答案为:25 , 15000.24.
7. 【解答】解:1+1+2=4,
180× =90(度),
该三角形是直角三角形;
或:1+2+2=5,
180× =72(度),
最大角为72 度,是锐角,所以该三角形的三个角都是锐角,即该三角形是锐角三角形;
答:该三角形是直角三角形或锐角三角形.
8. 【解答】解:360÷( 2+6× )
=360÷( 2+2)
=360÷4
=90(元)
90× =30(元)
答:篮球的单价是90 元.足球的单价是30 元.
故答案为:90,30.
9. 【解答】解:( 1)40×( 1+25%)
=40×125%
=50(米)
答:比40 米多25%是50 米.
(2)40÷( 1﹣20%)
=40÷80%
=50(米)
答:40 米比50 米少20%.
故答案为:50,50.
10. 【解答】解:10×( 1﹣25%)
=10×0.75
= 7.5(米)
答:剩7.5 米.
故答案为:7.5.
11. 【解答】解:28+32+30=90(棵),
(1000+1250)÷ 90
=2250÷90
=25(天),
1000﹣28× 25
=100﹣700
=300(棵),
答:丙在A 地植树300 棵.
故答案为:300.
二.判断题(共5 小题,满分5 分,每小题1 分)
12. 【解答】解:200×( 1+20%)× 80%
=200×120%× 80%
=192(元)
答:打折后价格是192 元.
故答案为:×.
13. 【解答】解:一个圆的半径扩大到原来的2 倍,面积扩大到原来的2×2= 4 倍,
所以题干的说法是错误的.
故答案为:×.
14. 【解答】解:1 米:1 厘米
=100 厘米:1 厘米
=100:1
1 米与1 厘米的比是1:1,计算错误;
故答案为:×.
15. 【解答】解:周长为2×4= 8(厘米);
面积为2×2=4(平方厘米);
周长与面积的单位不同,不能比较大小.
故答案为:×.
16. 【解答】解:根据分数的性质可知, = ,
但是的分母是10,所以它的分数单位是;
而的分母是5,所以它的分数单位是;
≠
所以,原题说法错误;
故答案为:×.
三.选择题(共5 小题,满分10 分,每小题2 分)
17. 【解答】解:3.14× 32×2,
= 3.14×9×2,
= 56.52(平方厘米),
答:分针扫过的面积是56.52 平方厘米.
故选:C.
18. 【解答】解:第一次:182÷5=36(瓶)⋯ 2(瓶),即可换得36 瓶汽水;
第二次:36+2=38(瓶), 38÷ 5=7(瓶)⋯ 3( 瓶),即可换得7 瓶汽水;
第三次:7+3=10(瓶), 10÷5=2(瓶),即可换得2 瓶汽水;
36+7+2 =45(瓶);所以总共可以换得45 瓶汽水.
故选:D.
19. 【解答】解:母鸡比公鸡多的只数是:
400× =250(只)
答:母鸡比公鸡多250 只.
故选:B.
20.【解答】解:根据轴对称图形的意义可知,圆、长方形、正方形是轴对称图形;三角形
中的等腰三角形、正三角形是轴对称图形,一般的三角形不是.
故选:B.
21. 【解答】解:每只小鸟需要1÷3= (元),
假设全是大鸟,那么小鸟有:
(100×3﹣ 100)÷( 3﹣ )
=200÷
=75(只)
100﹣75=25(只)
答:大鸟买了25 只.
故选:B.
四.计算题(共3 小题,满分27 分)
22. 【解答】解:
(1) = (2) = (3) 15× =5 (4)9÷ =12 ( 5) ÷15×
=
(6) + = (7) × 0.6= (8) ÷8= (9) ÷ = ( 10 ) ×
30+ ×30=30
23. 【解答】解:( 1)3x﹣ 8=16
3x﹣8+8=16+8
3x=24
3x÷3=24÷3
x=8
(2) x+0.7= 3.6
x+0.7 ﹣0.7= 3.6﹣ 0.7
x= 2.9
(3) 2.4×5﹣2x=6
12﹣ 2x=6
12﹣2x+2x= 6+2x
2x+6=12
2x+6﹣ 6=12﹣ 6
2x=6
2x÷2=6÷2
x=3
(4) x+2.8x= 4.56
3.8x= 4.56
3.8x÷ 3.8=4.56÷ 3.8
x= 1.2
(5)( 100﹣ x)÷ 5=4
(100﹣ x)÷ 5× 5=4×5
100﹣x= 20
100﹣ x+x=20+x
x+20= 100
x+20﹣20=100﹣20
x= 80
(6)5( x﹣ 1.8)= 18
5( x﹣ 1.8)÷ 5= 18÷5
x﹣ 1.8= 3.6
x﹣ 1.8+1.8= 3.6+1.8
x= 5.4
24. 【解答】解:( 1) 2.4×7.6+76× 0.66+7.6
= 2.4×7.6+7.6 ×6.6+7.6 ×1
=( 2.4+6.6+1 )× 7.6
=10×7.6
=76
(2) ﹣ [ ﹣( + ) ]
=
= ﹣( 1﹣ )
=
=0
(3)999× 99
=( 1000﹣ 1)× 99
=1000×99﹣1×99
=99000﹣99
=98901
(4) ﹣ +
=
=
=
=
=
(5) ﹣ + ﹣ + ﹣ + ﹣
=( )﹣( )
=
=2﹣1
=1
五.解答题(共2 小题,满分8 分,每小题4 分)
25. 【解答】解:
1﹣55%= 0.45, 1+63%= 1.63, 2.5× 40%=1,
8×1.25%= 0.1, 4.2÷60= 0.07, ×320%=2,
50%+ = 1.25, ﹣ 25%= 0.55.
26. 【解答】解:过D 作DM 平行于BF 交AC 于M(如图)
根据题意,作DM 与BE 平行,交AC 于M,
因为AF=DF,所以△ ABF 的面积与△ DBF 的面积相等
所以阴影部分的面积为△ DBF 的面积+△AEF 的面积
DM 平行于BE,所以△ DMC 相似△ CBE,所以CM:CE=CD:CB= 1:3
即EM= CE 因为EF 是△ ADM 的中位线, AE=ME,
所以AE= AC
所以△ ABE 的面积15× =6(平方厘米)
即阴影部分的面积(即△ DBF 的面积加△ AEF 的面积)等于6cm2
答:阴影部分的面积是6cm2.
六.应用题(共8 小题,满分32 分,每小题4 分)
27. 【解答】解:1800×( 1+ )
=1800× 1.25
=2250(台)
答:今年销售了2250 台.
28. 【解答】解:设大齿轮每分钟转x 圈,得
20×90=36× x
36x=1800
x=50
答:大齿轮每分钟转50 圈.
29. 【解答】解:4÷2=2(米)
2+1=3(米)
3.14×( 32﹣22)
= 3.14×( 9﹣4)
= 3.14×5
= 15.7(平方米)
答:石子路的面积是15.7 平方米.
30. 【解答】解:设至少要种x 棵树苗,
480÷ x×100%=96%
x=480÷ 0.96
x=500
答:至少应准备500 粒玉米种子.
31. 【解答】解:( 1﹣25%)÷ 25%
=75%÷25%
=3
(1﹣15%)÷ 15%
=85%÷15%
=
20÷( ﹣3)
=20÷
= 7.5(克)
答:这杯盐水原来含盐7.5 克.
32. 【解答】解:14﹣ [1﹣ ×( 14﹣ 2.5) ]
=14﹣ [1﹣ ]× 30
=14﹣ ×30
=14﹣12.75
= 1.25(天)
答:乙队休息了1.25 天.
33. 【解答】解:设两地的距离为x 千米.
[x﹣( ﹣ )× 50﹣25﹣ 30]÷50﹣ [x﹣( ﹣ )× 50﹣25﹣ 30]÷( 50+60)=
1
( x﹣ ﹣55)÷50﹣( x﹣
﹣55)÷ 110=1
( x﹣55)÷50﹣
( x﹣ 55)÷ 110=1
新六年级下册数学综合练习题( 含答案)(1)
一、选择题
1.0.80 m 和0.800 m( )测量得精确。
A. 0.80 m B. 0.800 m 一 C样. 精确
2.黑桃和红桃扑克牌各5 张,要想抽出3 张同类的牌,至少要抽出( )张.
A. 3 B. 5 C. 6
3.(5,6)表示( )
A. 五行六列 B五. 列六行 C不. 确定
4.如图,酒瓶中装有一些酒,倒进一只酒杯中,酒杯口的直径是酒瓶底面直径的一半,共能
倒满( )杯。
A. 18 B. 24 C. 30 D. 36
5.甲数比乙数少40%,甲乙两个数的比是( )
A. 3∶5 B. ∶2 5 C.∶ 4 1 D.∶ 1 4
6.种植场种西红柿公顷,相当于种黄瓜面积的,种黄瓜( )
A. 公顷 B. 公顷 C. 公顷 D. 公顷
7.一个成年人的身高相当于( )个人头部的长度。
A. 4 B. 5 C. 9 D. 13
8.棱长都是2 分米的正方体中,一个是木块,另一个是铁块。它们的体积相比()大。
A. 铁块 B木. 块 C同. 样
9.同样的书,甲读了全书的80%,乙读了全书的,两人谁读的多?( )
A. 甲 B乙. C一. 样多 D无. 法确定
10.在3:2 中,如果前项加上6,要使比值不变,后项应( )
A. 加上 6 B乘. 以 6 C乘. 以 3
11.一个直角三角形,两个锐角度数的比是1∶2,这两个锐角各是( )
A. 36 度,54 度 B. 30度,60 度 C. 40度, 50 度 D. 52度, 37
度
二、判断题
12.分母是7 的真分数都不能化成有限小数. ( )
13.下列三个图形的面积是相等的( )
14.一个数增加25%后,又减少25%,仍得原数. ( )
15.被除数÷ 24=10⋯⋯余数,被除数最大是249。( )
16.等底等高的圆柱体比圆锥体的体积大16 立方分米, 这个圆锥的体积是8 立方分米。( )
三、填空题
17.有120 名同学排队,每4 个人一行,排成了许多行,每相邻两行之间相隔1 米,你知道
这支队伍至少长________米吗?
18. (1) 的倒数是________.
(2) 的倒数是________.
19.一个盒子里装有黑、白两种颜色的跳棋各10 枚,从中最少摸出________枚才能保证有2
枚颜色相同,从中至少摸出________枚,才能保证有3 枚颜色相同。
20.6 个苹果放进5 个盘子中,总有一个盘子至少放________个苹果。
21.从1﹣24 中至少取出________ 个数,才能保证其中有两个数的差是5 的倍数.
22.时钟6 点敲6 下, 10 秒敲完;10 点敲10 下, ________秒敲完。
23.直接写出得数。
÷ =________ ×3=________6 × = ________ + ×7=________
100÷ 10%=________ ÷1=________ ÷7=________ × 9× =________
24.如图,把一个圆柱体切拼成一个长方体,表面积比原来增加了24 平方厘米,已知底面的
半径是2 厘米, 相信你一定能求出圆柱体的体积是________ 立方厘
米.
四、计算题
25.完成下面的竖式计算.
(1)
(2)
(3)
26.解比例。
(1)
(2)
(3)
(4)
五、解答题
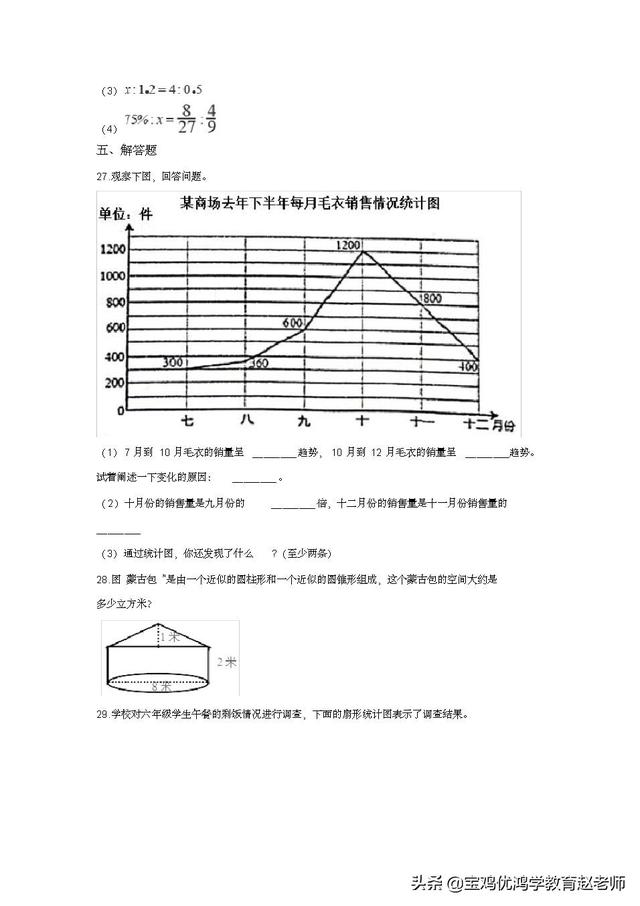
27.观察下图,回答问题。
(1)7 月到10 月毛衣的销量呈________趋势, 10 月到12 月毛衣的销量呈________趋势。
试着阐述一下变化的原因:________。
(2)十月份的销售量是九月份的________倍,十二月份的销售量是十一月份销售量的
________
(3)通过统计图,你还发现了什么?(至少两条)
28.图“蒙古包”是由一个近似的圆柱形和一个近似的圆锥形组成,这个蒙古包的空间大约是
多少立方米?
29.学校对六年级学生午餐的剩饭情况进行调查,下面的扇形统计图表示了调查结果。
(1)没有剩饭的人数占调查总人数的________%。
(2)在这次调查中, 剩饭量大约一半及超过一半的共有60 人。这次调查的总人数是________
人。
(3)小明看到上面的调查结果后说:“六年级同学在节约粮食方面做得还不错。”你同意他
的说法吗??简要说明理由。
30.学校把植树560 棵的任务按人数分配给五年级三个班, 已知一班有47 人,二班有48 人,
三班有45 人,三个班各植树多少棵?
31.港珠澳大桥是世界最长跨海大桥,东起香港,西止珠海,全长55 千米,一辆巴士从香港
出发,每小时行驶50 千米,一辆小轿车从珠海出发,每小时行60 千米, 两车同时出发后几
小时会相遇?(列方程解答)
答案解析部分
一、选择题
1.【答案】B
【考点】小数的近似数
【解析】【解答】解:0.80 精确到百分位, 0.800 精确到千分位, 0.800 m 测量得精确。
故答案为:B。
【分析】小数部分保留的位数越多,测量就更精确。根据小数部分数位的多少确定即可。
2.【答案】B
【考点】抽屉原理
【解析】【解答】解:2×2+1=5(张)
答:至少要抽出5 张.
故选:B.
【分析】从最极端情况进行分析:抽出的4 张,两种颜色各有2 张,这时再任取一张,即可
保证有抽出3 张同类的牌.
3.【答案】B
【考点】数对与位置
【解析】【解答】列在前,行在后【分析】考查了用数对表示位置的能力
4.【答案】C
【考点】圆柱的体积(容积) ,圆锥的体积(容积)
【解析】【解答】解:设酒瓶的底面直径是4,则酒杯口的直径是2,
4÷ 2=2,2÷ 2=1,2+3=5,
(π× 22)×÷5(π× 1×2)×
=20π÷ π
=20×
=30(杯)
故答案为:C。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高× , 酒瓶的高是5,酒杯的高是
2,可以设出酒瓶和酒杯口的直径,然后用酒瓶内酒的体积除以酒杯的容积即可求出倒满的
杯数。
5.【答案】A
【考点】比的应用
【解析】【解答】(1-40%):1=60%:1=60:100=3:5
故答案为:A
【分析】乙数是单位“1”,甲数就是(1-40%),由此写出两个数的比并化成最简整数比即可.
6.【答案】B
【考点】分数除法的应用
【解析】【解答】(公顷)
故答案为:B
【分析】题意可知,本题把种黄瓜面积看作单位“1”,种西红柿面积与种黄瓜面积存在以下
关系,总黄瓜面积=种西红柿面积( 公顷), 单位“1”未知,根据除法的意义,已知两
个因数的积和其中的一个因数,求另一个因数是多少,用除法即可解答。
7.【答案】C
【考点】长度的估算
【解析】【解答】解:一个成年人的上半身相当于3 个人头部的长度、下半身相当于5 个人
头部的长度,所以说一个成年人的身高相当于9 个人头部的长度。
故答案为:C。
【分析】估测长度:可以目测、可以通过生活经验、也可以用身体的某部分或身边的某物品
作为“尺”来估测。
8.【答案】C
【考点】正方体的体积
【解析】【解答】解:木块的体积是2×2×2=6立方分米,铁块的体积是2×2×2=6立方分米。
故答案为:C。
【分析】正方体的体积=棱长×棱长×棱长,所以无论是木块还是铁块,他们的体积相等。
9.【答案】C
【考点】百分数与分数的互化
【解析】【解答】=4÷5=0.8=80%,两人读的一样多。
故答案为:C。
【分析】根据题意可知,先将分数化成百分数,然后对比大小即可。
10.【答案】C
【考点】比的基本性质
【解析】【解答】解:3+6=9
9÷ 3=3
2× 3=6
6﹣2=4
即3:2 的前项加上6,要想使比值不变,后项2 也要乘3 或加上4.
故选:C.
【分析】根据比的基本性质, 3:2 的前项加上6,即3 加上6 后变为9 扩大了3 倍,要想使
比值不变,后项2 也要扩大3 倍变为6,即加上4;据此解答.
11.【答案】B
【考点】比的应用--按比分配
【解析】【解答】90°× =30(度);
90°× =60(度) .
故答案为:B.
【分析】根据题意可知, 直角三角形中两个锐角的度数和是90 度,依据两个锐角的度数比,
用锐角和×其中一个锐角占总和的分率=这个锐角的度数, 同样的方法, 可以求出另一个锐角
的度数,据此解答.
二、判断题
12.【答案】正确
【考点】小数与分数的互化,最简分数的特征
【解析】【解答】分母是7 的真分数都不能化成有限小数.正确
故答案为:正确
【分析】分母中只含有2 和5 的质因数的最简分数能化成有限小数,
13.【答案】正确
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解:第一个面积:ah,第二个面积:ah,第三个面积:2ah÷2=ah,面积相
等,原题说法正确。
故答案为:正确。
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,由此根据面积公式计算后判断即可。
14.【答案】错误
【考点】含百分数的四则混合运算
【解析】【解答】解:设这个数为x,
x×( 1+25%) ×(1﹣25%)
=0.9375x,
0.9375x< x;
所以一个数增加25%后,又减少25%,仍得原数的说法是错误的;
故答案为:错误.
【分析】本题出现了两个单位“1”,并且前后两个单位“1”不同,一个数增加25%后,是增加
一个数的25%;再减少25%,是减少增加后的数的25%,只要设出这个数为x,然后用x 表
示出结果,最后进行比较,即可得出结论.
15.【答案】错误
【考点】余数和除数的关系, 1000 以内的有余数除法
【解析】【解答】被除数最大是263。
【分析】根据整数的除法及应用,即得余数最大是23,故被除数最大是263。
16.【答案】正确
【考点】圆柱与圆锥体积的关系
【解析】【解答】解:等底等高的圆柱体比圆锥体的体积大16 立方分米, 这个圆锥的体积
是16÷2=8立方分米。
故答案为:正确。
【分析】等底等高的圆柱体是圆锥体体积的3 倍,那么等底等高的圆柱体比圆锥体的体积大
2 个圆锥体的体积,据此作答即可。
三、填空题
17.【答案】29
【考点】植树问题
【解析】【解答】120÷4=30(行)
间隔数:30-1=29
29× 1=29 (米)
18.【答案】(1)9
(2)20
【考点】倒数的认识
【解析】【解答】解:(1) 的倒数是9;
(2) 的倒数是20 。
故答案为:(1)9;(2)20。
【分析】乘积是1 的两个数互为倒数,分子是1 的分数的倒数就是这个分数的分母。
19.【答案】3;5
【考点】抽屉原理
【解析】【解答】解:2+1=3,最少摸出3 枚才能保证2 枚颜色相同;
2× 2+1=5,最少摸出5 枚,才能保证有3 枚颜色相同。
故答案为:3;5。
【分析】从最坏的情况考虑,假如前2 次摸出一个黑色和一个白色球,那么再摸出一个球
就能保证有2 枚颜色相同;假如前4 次各摸出2 个黑球, 2 个白球,那么再摸出一个就能保
证有3 每颜色相同。
20.【答案】2
【考点】抽屉原理
【解析】【解答】解:6÷5=1⋯⋯1 ,1+1=2(个)
故答案为:2【分析】假如5 个盘子每个盘子里各放1 个苹果,那么余下的1 个苹果无论放
进哪个盘子里总有一个盘子至少放2 个苹果.
21.【答案】6
【考点】公约数与公倍数问题,抽屉原理
【解析】【解答】解:1﹣24 中的各数除以5,
余数包括0,1, 2,3,4 这5 中情况,
然后再选任何1 个数都会有相同余数,
这个数的差就是5 的倍数,
所以答案是6 个,
故答案为:6.
【分析】1﹣24 中的各数除以5,取余数,余数包括0,1,2,3,4 这5 中情况.每种情况
下选1 个数, 此时还没有2 个数的差是5 的倍数. 根据抽屉原理, 然后再选任何1 个数都会
有相同余数,这个数的差就是5 的倍数,所以答案是6 个.
22.【答案】18
【解析】【解答】解:10÷(6-1) ×(10-1)
=10÷ 5×9
=18(秒)
故答案为:18
【分析】敲6 下有5 个间隔,敲10 下有9 个间隔,用10 除以5 求出每个间隔的时间,用
每个间隔的时间乘9 即可求出敲10 下需要的时间。
23.【答案】;1;;6 ;1000;;;2
【考点】分数乘法,分数除法
【解析】【解答】解:÷ = × = , ×3=1,6× = , + ×7=
+6=6 ,100÷ 10%=100÷ 0.1=1000, ÷1= , ÷7= , × 9× =2
故答案为:;1;;;1000;;;2
【分析】计算分数乘法时能约分的要先约分再乘, 计算分数除法时要把除法转化成乘法来计
算,计算混合运算时要先确定运算顺序.
24.【答案】75.36
【考点】圆柱的侧面积、表面积,立方体的切拼
【解析】【解答】解:24÷2÷2=6 (厘米);
3.14 ×2 2×6,
=3.14 ×4×,6
=3.14 ×2,4
=75.36(立方厘米) ;
答:圆柱体的体积是75.36 立方厘米.
故答案为:75.36.
【分析】把一个圆柱切开后拼成一个和它等底等高的近似长方体, 拼成的长方体表面积就比
圆柱多了两个长方形的面积, 这两个长方形的宽和圆柱的底面半径相等, 都是2 厘米, 长和
圆柱的高相等;已知表面积增加了24 平方厘米,就可求出高是多少厘米,进而再求出圆柱
的体积.此题是求圆柱的体积,必须先知道底面半径和高,才可利用“V=Sh”来解答.
四、计算题
25.【答案】(1)
(2)
(3)
【考点】多位小数的加减法
【解析】【分析】计算小数加、减法,先把各数的小数点对齐(也就是把相同数位上的数对
齐),再按照整数加、减法的法则进行计算, 最后在得数里对齐横线上的小数点点上小数点。
(得数的小数部分末尾有0,一般要把0 去掉.)
26.【答案】(1)40%x-20=140
解:0.4x=140+20
x=160 ÷ 0.4
x=400
(2)
解:1.8x=3.2
x=3.2 ÷ 1.8
x=
(3) x:1.2=4:0.5
解:0.5x=1.2 ×4
x=4.8 ÷ 0.5
x=9.6
(4) 75%:x=
解:
【考点】含百分数的四则混合运算, 综合应用等式的性质解方程, 应用比例的基本性质解比
例
【解析】【分析】解方程时根据等式的性质把方程两边同时加上同一个数或同时乘或除以同
一个非0 数;解比例时根据比例的基本性质把比例写成两个内项积等于两个外项积的形式,
然后根据等式的性质求出未知数的值。
五、解答题
27.【答案】(1)上升;下降;人们每年都会提前够买下一个季节的衣服
(2)2;
(3)我还发现:该商场十月份毛衣销售的最好,可以多进一些;该商场在十月之后可以少
进一些毛衣。
【考点】从单式折线统计图获取信息
【解析】【解答】解:(1) 7 月到10 月毛衣的销量呈上升趋势, 10 月到12 月毛衣的销量呈
下降趋势。试着阐述一下变化的原因:人们每年都会提前够买下一个季节的衣服;
(2)十月份的销售量是九月份的1200÷600=2 倍,十二月份的销售量是十一月份销售量的
800÷ 400= 。
【分析】(1)从图中可以看出7 月到10 月毛衣的销量呈上升趋势, 10 月到12 月毛衣的销
量呈下降趋势。因为毛衣是冬季穿的, 7 月到10 月还属于秋季, 而毛衣的销量呈上升趋势,
10 月到12 月属于冬季,毛衣的销量反而呈下降趋势,所以变化的原因可能是:人们每年都
会提前够买下一个季节的衣服;
(2)十月份的销售量是九月份的几倍=十月份的销售量÷九月份的销量,十二月份的销售量
是十一月份销售量的几分之几=十二月份的销售量÷十一月份销售量;
(3)可以根据每月毛衣销售的件数, 确定进的件数, 例如, 该商场十月份毛衣销售的最好,
可以多进一些;该商场在十月之后可以少进一些毛衣。
28.【答案】 解:3.14 ×(8÷2)2×2+3.14(×8÷2)2× 1×
=3.14 ×16×2+3.14×16×1×
≈ 100.48+16.75
=117.23 (立方米)
答:这个蒙古包所占的空间大约是117.23 立方米。
【考点】圆柱的体积(容积) ,圆锥的体积(容积)
【解析】【分析】这个蒙古包是由圆锥和圆柱组成,所以这个蒙古包的空间是圆锥的体积和
圆柱的体积, 圆柱的底面半径=底面直径÷2,圆柱的底面积=圆锥的底面积, 所以圆柱的体积
=πr2h,那么圆锥的体积= πr2h。
29.【答案】(1)55
(2)400
(3)解:400×55%=220(人)
400× 30%=120 (人)
400× 11%=44 (人)
400× 4%=16 (人)
同意小明的说法。六年级同学午餐有220 人没有剩饭, 120 人有少量剩饭, 44 人剩饭量大
约一半,仅有16 人剩饭量超过一半。总体来说,六年级同学在节约粮食方面做得还不错。
【考点】从扇形统计图获取信息,百分数的应用--运用乘法求部分量
【解析】【解答】( 1)1-(11%+30%+4%)
=1-45%
=55%
(2)60÷(11%+4%)
=60÷ 15%
=400(人)
【分析】(1)根据题意可知,把六年级接收调查的学生总人数看作单位 “1,”用 1-有少量剩
饭、剩饭量大约一半及剩饭量超过一半的学生占调查总人数的百分比=没有剩饭的人数占调
查总人数的百分比,据此列式解答;
(2)根据题意可知,把六年级接收调查的学生总人数看作单位 “1,”用剩饭量大约一半及
超过一半的总人数÷剩饭量大约一半及超过一半的占总人数的百分比=调查的总人数, 据此列
式解答;
(3)根据题意可知, 先用总人数×各种情况占总人数的百分比=各种情况的人数, 然后对比
即可解答.
30.【答案】解:总份数为47+48+45=140 一班植树:560× =188(棵) 二班植树:
560× =192(棵) 三班植树:560× =180(棵) 答:一、二、三班分别植树
188 棵、192 棵、180 棵。
【考点】比的应用--按比分配
【解析】【分析】将560 棵树看作单位1,三个班的总人数=一班人数+二班人数+三班人数
=47+48+45=140(人),所以将单位1 平均分为140 份,树的总棵树× (一班的人数占总
人数的份数) =一班植树的棵树;树的总棵树× (二班的人数占总人数的份数) =二班植
树的棵树;树的总棵树× (三班的人数占总人数的份数) =三班植树的棵树;代入对应
的数字即可得出答案。
31.【答案】解:设两车同时出发x 小时后会相遇。
(50+60)x=55
x=55 ÷ 110
x=0.5
答:两车同时出发0.5 小时后会相遇。
【考点】列方程解相遇问题
【解析】【分析】等量关系:速度和×相遇时间=路程,先设出未知数,再根据等量关系列方
程解答即可。
【数学】小升初数学试卷及答案( 人教版)
数学小升初衔接培优训练二:数的整除
一、填空题(共6 题;共27 分)
1.有一张长48 厘米,宽36 厘米的长方形纸,如果要裁成若干同样大小的正方形
而无剩余,裁成的小正方形的边长最大是____ ____厘米.
2.A=2 ×3×5,B=3×5×7,A 和B 的最大公因数是________,最小公倍数是________.
3.如果a÷b=10,(a、b 都是非0 自然数),则a 和b 的最大公约数是________,
最小公倍数是________
A.a B.b C.10 D.1.
4.一个五位数8□35△,如果这个数能同时被2、3、5 整除,那么□代表的数字是
________ ,△代表的数字是________ .
5.有一个四位数3AA1 能被9 整除, A 是________ .
6.有三个连续的自然数,其中最小的能被3 整除,中间的能被5 整除,最大的能
被7 整除,请写出一组符合条件的数________ .(答案不唯一)
二、单选题(共5 题;共15 分)
7.用大小相等的长方形纸,每张长12 厘米,宽8 厘米.要拼成一个正方形,最
少需要这种长方形纸( )
A. 4 张 B. 6张 C. 8张
8.甲每3 天去少年宫一次, 乙每4 天去一次,丙每6 天去一次,如果6 月1 日甲、
乙、丙同时去少年宫,则下次同去少年宫应是( )
A. 6 月12 日B. 6 月13 日C. 6 月24 日
D. 6 月25 日
9.下列各组数中,第二个数能被第一个数整除的是( )
A. 2.5 和5 B. 4 和10 C. 0.4 和
1.2 D. 5 和25
10.车库里面有8 间车房,顺序编号为1,2,3,4,5,6,7,8.这车房里所停
的8 辆汽车的车号均为三位数且恰好是8 个连续整数.已知每辆车的车房号都能
被自己的车号整除,车号尾数是3 的汽车车号为( )
A. 853 B. 843 C. 863
11.有5 张卡片上面的数字分别是0,4,5,6,7,从中抽出3 张组成所有三位数
中能被4 整除的有( )
A. 11 B. 12 C. 10
D. 15
三、综合题(共9 题;共58 分)
12.四位数A752 是24 的倍数, A 最大是几?
13.若“AB59A”能被198 整除,求( A+B )的和.
14.食品店买来85 个面包,如果每2 个装一袋,能正好装完吗?如果每5 个装一
袋,能正好装完吗?为什么?
15.小红和妈妈在中心广场锻炼, 妈妈跑一圈用6 分钟,小红跑一圈用8 分钟.她
们同时从起点出发,他们几分钟后可以在起点第一次相遇?
16.如图, 7 个小朋友围成一圈依次报数,小强报1,小兵报2,小丽报3⋯照这
样谁最先报到7 的倍数?其他小朋友有可能报出7 的倍数吗?
17.两根钢筋分别长为24 米和18 米,现把它截成同样长的小段,且无剩余,每
段最长可截成多少米?一共可截成多少段?
18.老师买回一些学习用品(数量相同) .老师付给营业员100 元,找回28 元,
请问找回的钱对不对,你是怎么判断出来的?
19.有7 袋米,它们的重量分别是12、15、17、20、22、24、26 公斤.甲先取走
一袋,剩下的由乙、丙、丁取走.已知乙和丙取走的重量恰好一样多,而且都是
丁取走重量的2 倍.那么甲先取走的那一袋的重量是多少公斤?
20.一个房间的长是3.6 米,宽是2.4 米.现在要在这个房间铺上相同的方砖.
(1)每块方砖的边长最大是多少分米?
(2)这间房间一共需要多少块这样的方砖?
答案解析部分
一、填空题
1.【答案】12
【考点】公因数和公倍数应用题
【解析】【解答】解:把48 和36 分解质因数:48=2×2×2×2×3,
36=2×2×3×3,
48 和36 的最大公因数是2×2×3=12;
答:裁成的小正方形的边长最大是12 厘米;
故答案为:12.
【分析】根据题意可知,求剪出的小正方形的边长最大是几厘米.也就是求48
和36 的最大公因数,先把这两个数分解质因数,它们公有质因数的乘积就是它
们的最大公因数.由此解答.
2.【答案】15;210
【考点】求几个数的最大公因数的方法,求几个数的最小公倍数的方法
【解析】【解答】解:A=2×3×5,B=3×5×7, A 和B 的最大公因数是:3×5=15;
A 和B 的最小公倍数是:3×5×2×7=210.
故答案为:15,210.
【分析】求两个数的最大公因数和最小公倍数, 首先把这两个数分解质因数, 公
有质因数的乘积就是这两个数的最大公因数;最小公倍数是公有质数与各自独有
质因数的连乘积;因此解答.
3.【答案】B;A
【考点】求几个数的最大公因数的方法,求几个数的最小公倍数的方法
【解析】【解答】解:a÷b=10,(a、b 都是非0 自然数),据此可知ab 是倍数关
系, a 为较大数, b 为较小数,
所以a 和b 的最大公约数是b,最小公倍数是a;
故选:B,A.
【分析】如果a÷b=10,(a、b 都是非0 自然数),据此可知a、b 是倍数关系,根
据倍数关系的两个数的最大公约数是较小数, 最小公倍数是较大数, 即可解答.解
答本题关键是由a÷b=10,(a、b 都是非0 自然数),知ab 是倍数关系,然后根据
被关系的最大公因数和最小公倍数的求法解答.
4.【答案】2 或5 或8;0
【考点】整除的性质及应用
【解析】【解答】解:8+3+5=16;
三角形代表的数字在个位数,必须是0;
□代表的数字可以是2 或5 或8,才能被3 整除;
故答案为:2 或5 或8,0.
【分析】能同时被2、3、5 整除的数,必须具备:被2、5 整除个位上的数只能
是0,各个数位上的数的和能够被3 整除;现在8+3+5=16,代表的数字可以是2
或5 或8,符合条件.此题属于考查能同时被2、3、5 整除的数的特征,记住特
征,灵活解答.
5.【答案】7
【考点】数的整除特征
【解析】【解答】解:根据题意可得:
四位数3AA1 ,它能被9 整除,那么它的数字和( 3+A+A+1 )一定是9 的倍数;
因为A 是一个数字,只能是0、1、2、3、⋯、9 中的某一个整数,最大值只能
是9;若A=9,那么3+A+A+1=3+9+9+1=22 ,22<27,所以, 3AA1 的各位数字
和只能是9 的1 倍或2 倍,即9 或18;
当3+A+A+1=9 时, A=2.5,不合题意;
当3+A+A+1=18 时,A=7,符合题意;
所以, A 代表7,这个四位数是3771.
答:A 是7,
故答案为:7.
【分析】已知四位数3AA1 能被9 整除,那么它的数字和( 3+A+A+1 )一定是9
的倍数然后再根据题意进一步解答即可.因为A 是一个数字,只能是0、1、2、
3、⋯、9 中的某一个整数,最大值只能是9.若A=9,那么3+A+A+1=22 ,22
<27,所以3AA1 的各位数字和只能是9 的1 倍或2 倍,即9 或18.
6.【答案】159,160,161
【考点】数的整除特征
【解析】【解答】解:这三个连续整数在100﹣200 之间,故其百位数字确定为1.由
于中间数能被5 整除,故其末位数为0 或5,
所以,最小数的百位数字为1,个位数字为9 或4;
若最小数的个位数字为9,由其能被3 整除,故其十位数字为2、5、8;
若最小数的个位数字围,由其能被三整除,其十位数字为1,4,7;
从而,最小数只可能是129,159,189,114,144,174 中的某几个数130,160,
190,115,145,175 已能被5 整除,故只须从131,161,191,116,146,176
中筛选出能被7 整除的数,
即:上述六数中只有161=7×23 满足要求;
所以所求连续三数为159,160,161;
故答案为:159,160,161.
【分析】三个自然数的百位数字都是1,由于中间的数能被5 整除,故中间数的
个位数字只能是0 或5,从而最小的数的末位数字只能是9 或4(即10﹣1=9,5
﹣1=4);下一步可利用被3 整除的数的特征确定其十位数字, 最后再用牧举法确
定这3 个连续整数即可.
二、单选题
7.【答案】B
【考点】求几个数的最小公倍数的方法,图形的拼组
【解析】【解答】解:(24÷12)×(24÷8)
=2×3
=6(张)
答:需要6 张.
故选:B.
【分析】12 和8 的最小公倍数是24,所以拼成后正方形边长是24 厘米,需要小
长方形的长的个数是24÷12,需要小长方形宽的个数是24÷8.需要这种纸的张数
就是( 24÷12)×(24÷8).据此解答.
8.【答案】B
【考点】公因数和公倍数应用题
【解析】【解答】解:把4、6 分解质因数:
4=2×2;
6=2×3;
~4、6 的最小公倍数是:2×2×3=12;
他们再过12 天同去少年宫;
1+12=13(日),即6 月13 日.
故选:B.
【分析】根据题意,是求3、4、6 的最小公倍数,就是求4、6 的最小公倍数,
首先把这两个数分解质因数, 它们的公有质因数和各自独有质因数的乘积就是它
们的最小公倍数,然后进行推算日期即可.此题属于求最小公倍数问题,求3
个数的最小公倍数, 利用分解质因数的方法, 它们的公有质因数和各自独有质因
数的乘积就是它们的最小公倍数.
9.【答案】D
【考点】整除的性质及应用
【解析】【解答】解:A、2.5 和5;
2.5 是小数,只能说5 能被2.5 除尽;
B、4 和10;
10÷4=2⋯2,有余数, 10 不能被4 整除;
C、0.4 和1.2;
0.4,1.2 都是小数,只能说1.2 能被0.4 除尽;
D、5 和25;
25÷5=5,25 能被5 整除;
故选:D.
【分析】整除就是指:若整数“a” 除以大于0 的整数“b”,商为整数,且余数为零,
我们就说a 能被b 整除;整除都是对于整数而言的.
10.【答案】B
【考点】整除性质
【解析】【解答】解:1,2,3,4,5,6,7,8 的最小公倍数是840,
因为840 加上1~8 中的某个数后必能被这个数整除,所以8 辆汽车的车号依次
为841~848.
故车号尾数是3 的汽车车号是843.
答:尾数是3 的汽车车号是843.
故选:B.
【分析】1,2,3,4,5,6,7,8 的最小公倍数是840,840 加上1~8 中的某
个数后必能被这个数整除,所以8 辆汽车的车号依次为841~848.据此即可解
答问题.
11.【答案】D
【考点】整除的性质及应用,公约数与公倍数问题
【解析】【解答】解:能被4 整除,那么最后两位数能被4 整除(因为100 的倍
数都能被4 整除),
这样,最后两位只能是:04,40,56,60,64、76 六种.
当最后两位数为04 时:百位在5,6,7 选一个,三种;
当最后两位数40 时:百位在5,6,7 选一个,三种;
当最后两位数56 时:百位在4,7 选一个,两种;
当最后两位数为60 时:百位在4,5,7 选一个,三种(因为百位数不为0);
当最后两位数为64 时:百位在5,7 选一个,两种(因为百位数不为0);
当最后两位数76 时:百位在5,4 选一个,两种;
所以共有3+3+2+3+2+2=15 种.
故选:D.
【分析】利用被4 整除的特征:当一个数的末两位能被4 整除,这个数就能被4
整除,由此特征分类讨论即可解决问题.
三、综合题
12.【答案】解:24=3×2×2×2,A752 应该能被3 整除.
四位数A752 是24 的倍数,
A+7+5+2=14+A 能被3 整除.
那A 只可能是:7、4、1,
因为A 在千位上,所以A 最大是7.
【考点】整除的性质及应用
【解析】【分析】24 分解成:3×2×2×2 因此:A752 应该能被3 整除. 也就是
A+7+5+2=14+A 能被3 整除. 那A 只可能是:7、4、1 所以,试算一下可得,
A 最大为7.
13.【答案】解:A+B+5+9+A=2A+B+5=9
(A+5+A )﹣( B+9)=2A﹣B﹣4=0
解得A=2 B=0
那么A+B=2+0=2
【考点】数的整除特征
【解析】【分析】198=2×9×11,
要是能被9 整除,则A+B+5+9+A 是9 的倍数,
2A+B+5 是9 的倍数;
能被11 整除,那么(A+5+A )﹣( B+9)=2A﹣B﹣4 是11 的倍数
14.【答案】解:85 个面包,如果每2 个装一袋,不能正好装完,因为85 的个位
上是5,所以85 不能被2 整除;
如果每5 个装一袋,能正好装完,因为85 的个位上是5, 所以85 能被5 整除;
答:如果每2 个装一袋,不能正好装完;如果每5 个装一袋,能正好装完.
【考点】整除的性质及应用
【解析】【分析】能被2 整除的数的特征:个位上是0、2、4、6、8 的数;能被
5 整除的数的特征:个位上是0 或5 的数;再根据能被2、5 整除的数的特征进
行判断能否正好装完.此题考查能被2、5 整除的数的特征及其运用.
15.【答案】解:6=2×3, 8=2×2×2,
所以6 和8 的最小公倍数是:2×3×2×2=24(分钟),
答:他们24 分钟后可以在起点第一次相遇
【考点】公因数和公倍数应用题
【解析】【分析】妈妈回到起点用的时间是6 分钟的整数倍,小红回到原地是8
分钟的整数倍,则第一次同时回到起点就是6 和8的最小公倍数分钟,因此得解.
16.【答案】解:小红最先报到7 的倍数.
因为只有7 个小朋友, 像这样一直进行下去, 只有小红能报到7 的倍数, 其他小
朋友报的数不可能是7 的倍数.
【考点】整除的性质及应用
【解析】【分析】一共是7 个小朋友,根据报数方法,可知小红最先报到7 的倍
数.由题意可知7 个数字一循环,依此即可作出判断.
17.【答案】解:24=2×2×2×3
18=2×3×3
24 和18 的最大公因数是2×3=6
24÷6=4
18÷6=3
4+3=7(段).
答:每段最长可截成6 米,一共可截成7 段
【考点】公因数和公倍数应用题
【解析】【分析】根据题意,可计算出18 与24 的最大公约数,即是每根小段的
最长,然后再用18 除以最大公约数加上24 除以最大公约数的商, 即是一共截成
的段数,列式解答即可得到答案. 解答此题的关键是利用求最大公约数的方法计
算出每小段的长度,然后再计算每根钢筋可以截成的段数,再相加即可.
18.【答案】解:花了:100﹣28=72(元),
因为学习用品的数量都相同,所以花的钱数应是10+5+3=18 的倍数,
72 是18 的4 倍,即买回的一些学习用品的数量都是4,
所以,找回的钱对.
答:找回的钱对.
【考点】找一个数的倍数的方法,求几个数的最小公倍数的方法
【解析】【分析】根据题意可知,花了100﹣28=72 元,因为学习用品的数量都相
同,所以花的钱数应是10+5+3=18的倍数,所以判断72 是否是18 的倍数即可.本
题主要考查求一个数的倍数是方法.找出花的钱数是否是18 的倍数是解答本题
的关键.
19.【答案】解:由于剩下的由乙、丙、丁三人买走,乙和丙买走的重量恰好相
等,都是丁的2 倍,
即乙,丙,丁三人买走的重量比为2:2:1,
所以,甲买走一袋后剩下的重量应是2+2+1=5 的倍数.
而总重量为:12+15+17+20+22+24+26=136千克,
从136 中减去一个数后和得数能被5 整除,则这个这个数的个位数字一定是1
或者6,
这7 袋大米的重量中只有26 的个位是6,
所以,甲买走的那一袋大米的重量是26 千克.
答:甲买走的那一袋大米的重量是26 千克.
【考点】数的整除特征
【解析】【分析】因为乙和丙买走的重量一样多,且都是丁的2 倍,所以乙丙丁
三人买走的重量是丁的5倍;而7袋大米的总重量是12+15+17+20+22+24+26=136
千克,从136 千克里减去5 的倍数,剩下的就是甲买走的重量.反过来说,从
136 千克里减去甲买走的那一袋大米的重量,剩下的重量一定是5 的倍数,要使
136 减去一个数后和得数能被5 整除,这个数的个位数字一定是1 或者6,而这
7 袋大米的重量中只有26 的个位是6,因此甲买走的那一袋大米的重量是26 千
克
20.【答案】(1)解:3.6 米=36 分米, 2.4 米=24 分米,
36=2×2×3×3,
24=2×2×2×3,
36 和24 的最大公约数是2×2×3=12,
答:每块方砖的边长最大是12 分米
(2)解:(36×24)÷(12×12)
=864÷144
=6(块)
答:这间房间一共需要6 块这样的方砖
【考点】公因数和公倍数应用题
【解析】【分析】(1)3.6 米=36 分米, 2.4 米=24 分米,要求每块方砖的边长最
大是多少分米, 就是求36 和24 的最大公约数;(2)要求这间房间一共需要多少
块这样的方砖, 用房间的面积除以每块方砖的面积即可. 解答此题的关键是运用
求最小公倍数的方法求出每块方砖边长,进而解决问题.






























































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








