
又来水一波文了,最近改写的没写,想法不少一个写不了唉,先祝大家中秋国庆双倍快乐。----2020.09.30
三次方程嘛,高中题有极低概率出现,因式分解的时候也喜欢出(因为三次方程的因式分解需要猜根或者得出一个解),学完一元二次方程的时候我也会对其感兴趣,那么我就用人话写一些关于一元三次方程的解法。
什么是一元三次方程?由一元二次方程的一般情况
当然,如果
- 一元三次方程有三个根,既是它们可以包含复数根,而且至少有一个实数根。
- 三次方程的韦达定理:

一.从最简单开始
如果三次方程有三个完全一样的根呢?那么类似一元二次方程我们可以知道它一定可以写成完全立方的形式,也就是
对比原方程的系数我们可以得到

消去

还有


当然,还可以列举更多.这里,我们把

那么我们可以自豪地说:这个三次方程有三个完全相同的根!为了方便,我们可以把它们记作
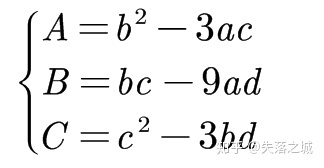
...
当然,你随手一写的三次方程几乎是碰不到三个完全相同的根的情况的,毕竟要满足的条件太苛刻了,我们就退而求其次:如果这个方程只有两个相同的根呢?
二.退而求其次
方程只有两个相等的根了!我们这个时候从韦达定理入手!因为
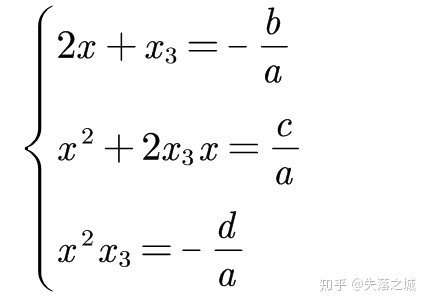
这个方程可不可以解出一些东西呢?仔细思索发现:可以!
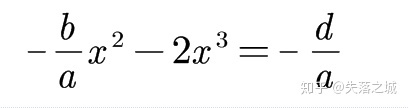
这里我们可能会想:怎么还是三次方程!
或者我们可以带入第二个式子得到

或者把第三个式子消去
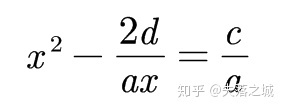
把它们整理好列出来,我们可以得到
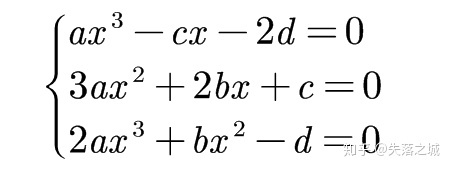
毋庸置疑,这三个方程是我们消去
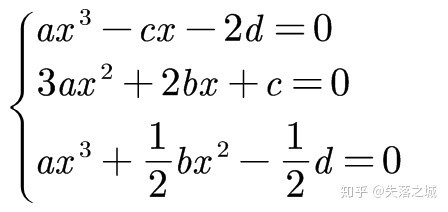
把(3)-(1)得到
当然,我们化简得到的方程是二次方程,依然存在一个增根,因此我们考虑和(2)相减消去二次项.假定
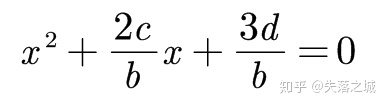
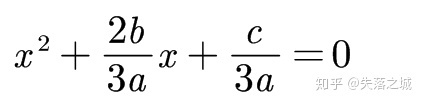
相减得到
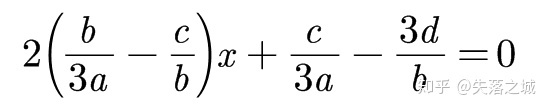
最后化简得到

看!又出现了前面我们的

相减,并且除去
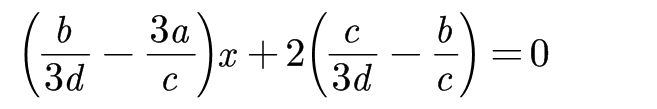
也即

看!又出现了
..
..
..
如果到这里就结束那也太没有意思了,根据前面的结果,如果一元三次方程有两个相等的根,那么它的根就是
这个式子说明了如果
三.最难的一步
三次方程的特殊情况至此讨论的差不多了,如果三次方程没有重根,那么我们把它叫做一般三次方程,而我们可以从缺项的三次方程开始讨论,如果三次方程少掉二次项或者一次项,那么也许问题会简单一点?我们考虑简化的方程
但是...有时候在无意之中也可能会遇到希望之花.
当我们在考虑
的时候,偶然发现
我们对比两个方程的系数得到

整理得到

看!这里明显是一个以
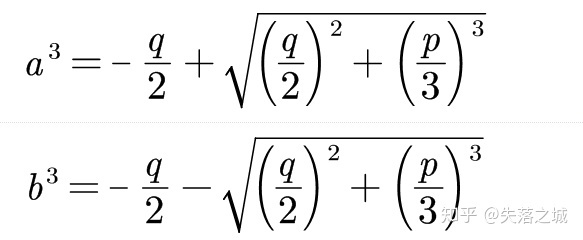
我们开立方得到

所以

非常美观
四.结束了
我们解开了形如
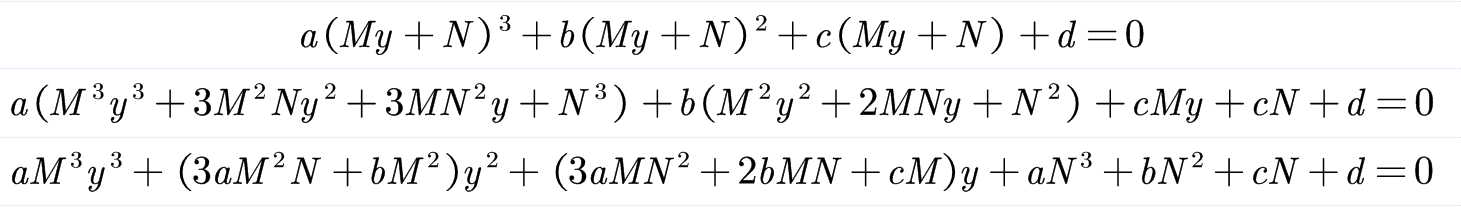
即
五.结束了?
记得最开始提出的一个最基本的性质:一元三次方程有三个根,可是按照上面的方法我们只能得到一个解,那么剩下的去哪了?(虽然我们可以根据韦达定理列出一元二次方程).这就得讲到一个重要的概念了:单位根.
讲一个简单的例子:我们尝试解决
,因此可以解得

没错,这正是三个单位根!
回到
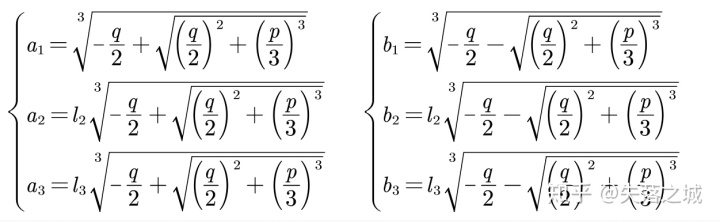
那么

因此大功告成!
六.新的时代
我们得到了新的公式!马上用来练练手吧!我随便写了一个方程
并且根据上述组合得到原方程的三个解为
呼!太壮观了.
然而在解决某些问题时候可能遇到了点麻烦,比如解方程
七.后记
时光流逝,当初的世界性难题在此看来不过是茶余饭后的思考题罢了,我们从中应该要了解到的不是三次方程本身,而是这种敢于探索另辟蹊径的精神和纪念人们在数学发展的历程中所做出的努力和贡献,也许三次方程问题本身并不会改变世界,但是它的“荒谬结果”却大大加快了复数理论的发展和壮大...感谢观看!如果有想要补充的有空我会考虑补充的.







 本文以通俗易懂的方式介绍了如何解一元三次方程,包括有重根的情况。通过韦达定理和特殊形式的方程,解析了一元三次方程的解法,探讨了单位根在解决此类问题中的应用。
本文以通俗易懂的方式介绍了如何解一元三次方程,包括有重根的情况。通过韦达定理和特殊形式的方程,解析了一元三次方程的解法,探讨了单位根在解决此类问题中的应用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








