点击上方蓝字“高中数学xyz”一起玩耍
公切线是指同时相切于两条或两条以上的曲线的直线。和两个圆相切的直线叫做这两个圆的公切线。如果两个圆在公切线的同侧,则这公切线叫外公切线;如果两个圆在公切线的异侧,则叫内公切线。
我们都熟知两个圆的位置关系无外乎五种情况:
相离、外切、相交、内切和内含.
那么如何去求两个非内含的两个圆的公切线方程呢?下面以两个相离的圆为例,浅谈公切线方程的两种求法。

解法一


解法二




解法一是常规的求两圆公切线的方法,而解法二用到的原理如下:
(1)求两圆内公切线方程的求法如下图:

(2)求两圆外公切线方程的求法如下图:

当两圆外切时,有一内公切线,且垂直两圆的连心线;
当两圆内切时,有一外公切线,且垂直两圆的连心线.
这两种公切线方程求解很容易,此处略.
再如:


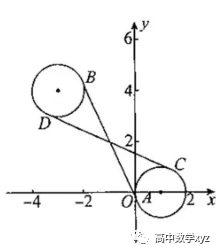


























 2684
2684

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








