各种触发器的特性方程_你也可以理解“麦克斯韦方程组”

自然和自然的规律隐藏在茫茫黑夜之中。上帝说：让牛顿降生吧。于是一片光明。——亚历山大·蒲柏

上帝又说：还要有光，于是便有了麦克斯韦方程组。

图片来源：http://mentalfloss.com

位于苏格兰爱丁堡城堡山谷的一侧有一条大街，乔治大街, 因国王乔治而得名。在乔治大街的末端有一座雕像——詹姆斯·克拉克·麦克斯韦, 苏格兰最杰出的科学家之一，今天我们要说的就是以他命名的一组方程。

一、基本知识准备

自然界中有很多的现象，如果仔细观察，会觉得特别有意思。比如每天抬头都能看到的太阳：

你、我能安心的在这刷知乎，很大程度上拜它所赐，太阳光是地球能量的主要来源，距离太阳1天文单位的位置（也就是在或接近地球），直接暴露在阳光下的每单位面积接收到的能量，其值约相当于

（瓦每平方米），也就说接收的能量是和面积是成正比的，——在这闷热的夏天，这位小姐姐你觉得热，是因为你暴露太多——

穿的太少了，当然由于地球附近星际空间中有大量的粒子的阻挡，到达你的身上的辐射已经小了很多。太阳是我们最常见的一种模型：中心对周围的 辐射作用。

当然还有其他的一些自然现象，比如经常骚扰沿海同胞的台风：

台风发源于热带海面，那里温度高，大量的海水被蒸发到了空中，形成一个低气压中心。随着气压的变化和地球自身的运动，流入的空气也旋转起来，形成一个逆时针旋转的空气漩涡，这就是热带气旋。只要气温不下降，这个热带气旋就会越来越强大，最后形成了台风。台风是我们最常见的另一种模型：中心对周围的旋转作用。

相信大家都走过环山路，小编前两天去了一趟恩施大峡谷，50公里的路要开2个多小时，不明所以的童鞋还以为司机在绕路呢？——实际司机就是在“绕路”，但是不得不饶。

在课堂上，老师问同学们：假设你要去爬座山，海拔是2000米，你要选择怎样上去最省力气？小明眼睛一转，说：我坐索道上去.......老师：小明，你...出...去！这是属于开挂，不算数。老师倒也难为同学们了：若选择最陡的那条路呢？距离是近了，但是费力气啊；要是选择多绕几圈呢，倒是不那么费力气了，但是距离远多了，这真是一个费脑子的问题。现在我们假如要去救援，时间最宝贵，要求距离最短，你该怎么办？——那就要选最陡的那条路，——那什么是陡？山路是我们最常见的第三种模型：前进的方向选择问题。

---

二、散度、旋度及梯度

万有引力定律其实胡克是有很大贡献的，但冠名权却属于牛顿，为什么？因为牛顿数学牛逼啊，光有想法不行，你得能用数学表达出来，才能让人信服。接下来我们就看看，数学家是如何描述上面几个问题的。

2.1 散度

前面我说道，我们每时每刻都在接收太阳带给我们的能量，在地球附近，直接暴露在阳光下的每单位面积接收到的能量，其值约相当于

（瓦每平方米），那太阳每秒钟会向外辐射多少能量呢？

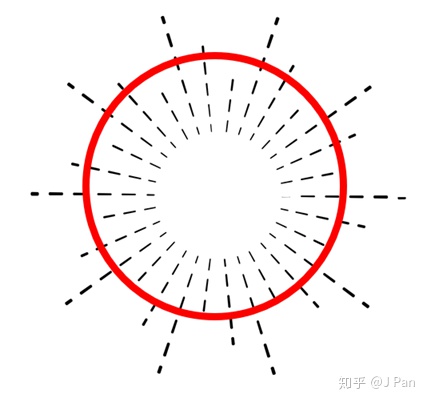
沿着太阳表面，作一条封闭曲线，把曲线上的

（不妨把光线的方向也考虑进来）给加起来，这不就是总的能量了吗？——我们也给它起个名字，就叫

通量吧，通过表面的总量，很显然，这一个 标量。数学表达式就是：

就是通过此曲线的通量，常识告诉我们，如果这个曲线是封闭的，不管这个曲线多大，长成什么样子，只要里面的太阳没变，这个通量就是个恒定值。

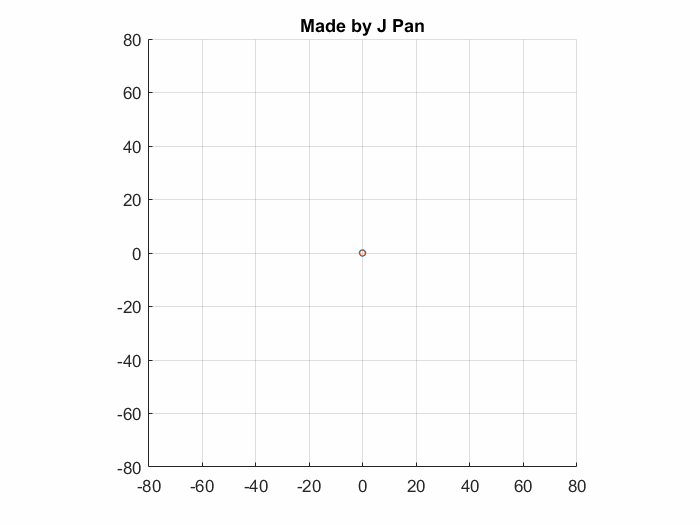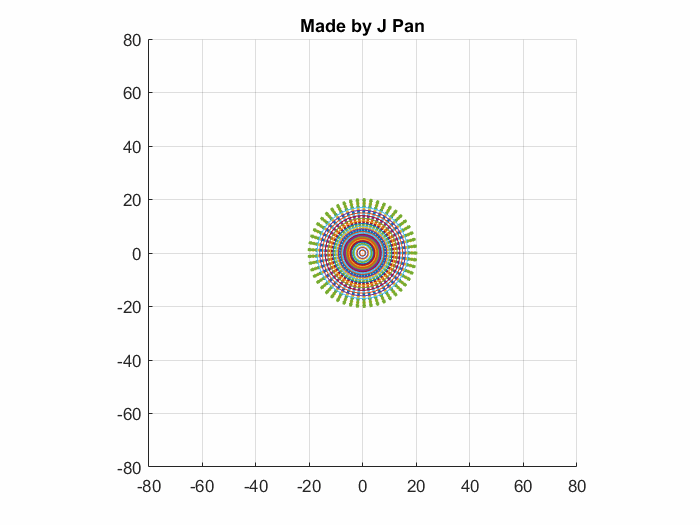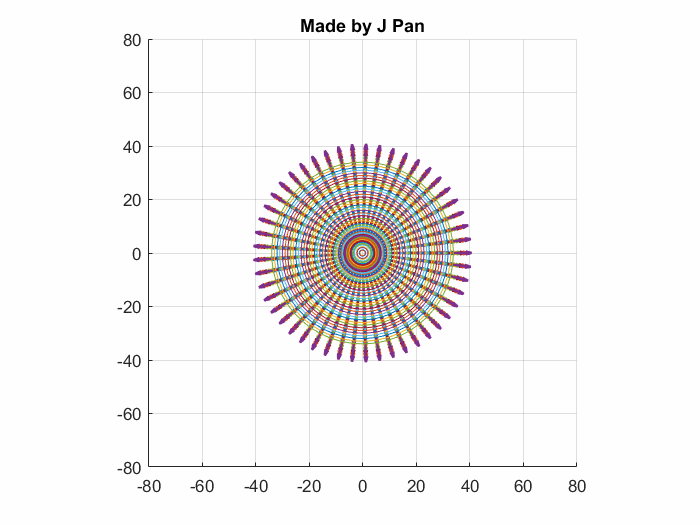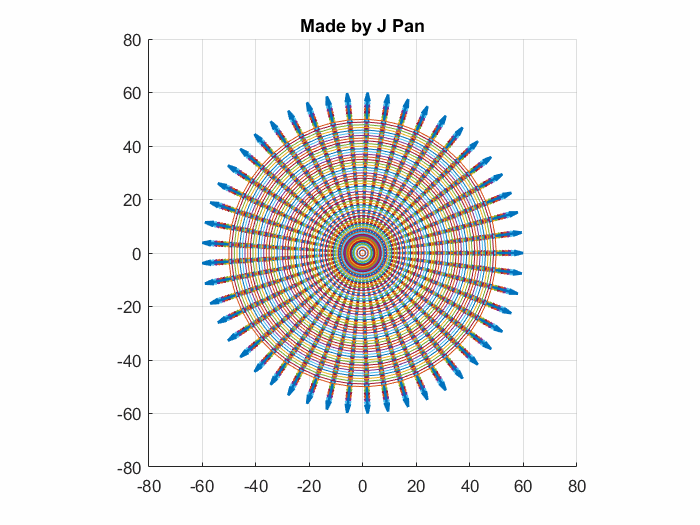
但实际太阳不是一个圆，而是一个球，所以我们要把封闭曲线扩展成封闭的曲面：

虽然太阳对于我们来说很大，放在整个在整个宇宙里面就非常渺小了——就是一小点点而已。假如不是以地球视野，而是以宇宙的视野来看太阳的的辐射，它那点通量如果还用一个封闭的曲面来算的话，那就显得太多余了——就一个“点点”啊！

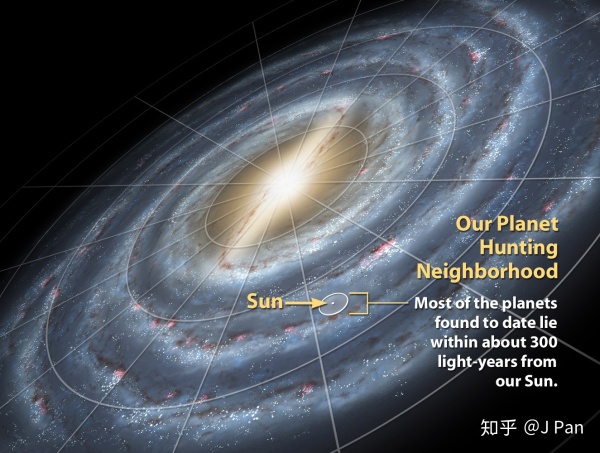
图片来源：http://sciencevibe.com

好了，封闭曲面开始瘦身了，一直缩小到极限为0，用此时的通量，除以封闭曲面所围体积，就能得到此点的辐射强度：

其中，

为封闭曲面

围成的区域，

这就是

点的散度。散度有什么意义呢？—— 它代表了某种“源”。这个“源”产生的向量场，散度如果是正的，代表向量场是往外散出的；如果是负的，代表向量场是往内集中的，散度的大小，代表这个“源”的强弱。

2.2 旋度

我们要解决的，不仅有辐射，还有漩涡。

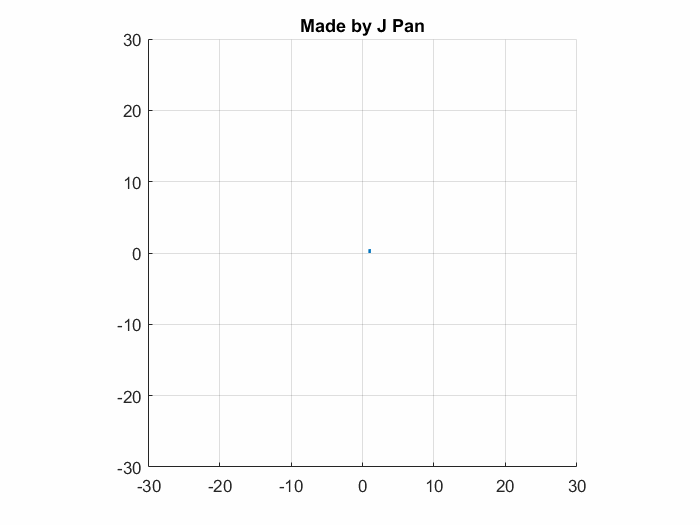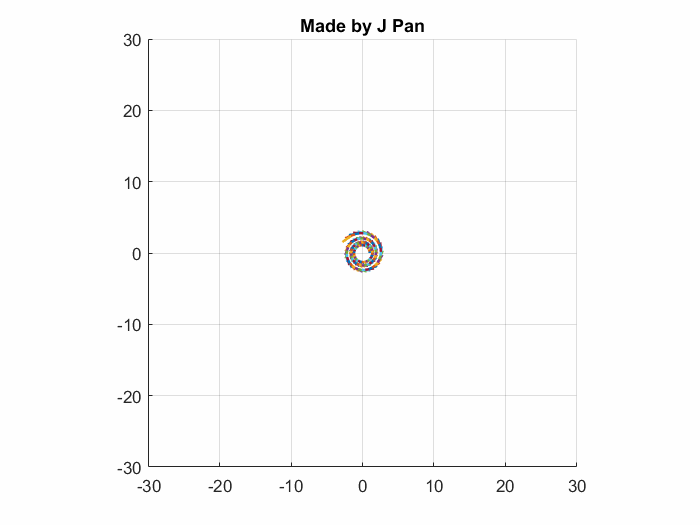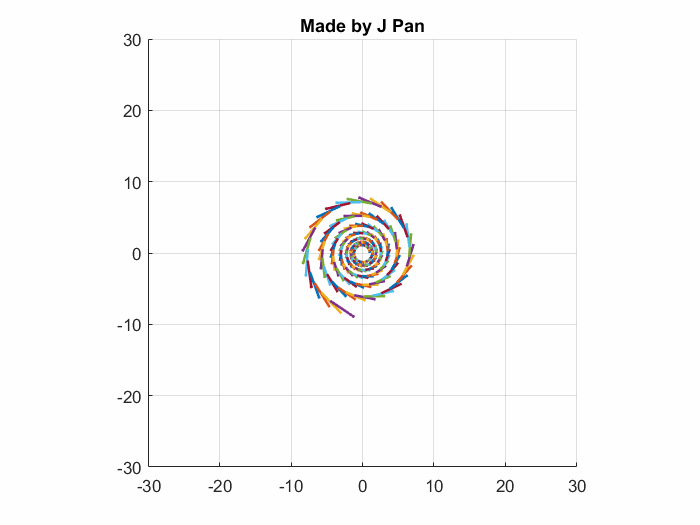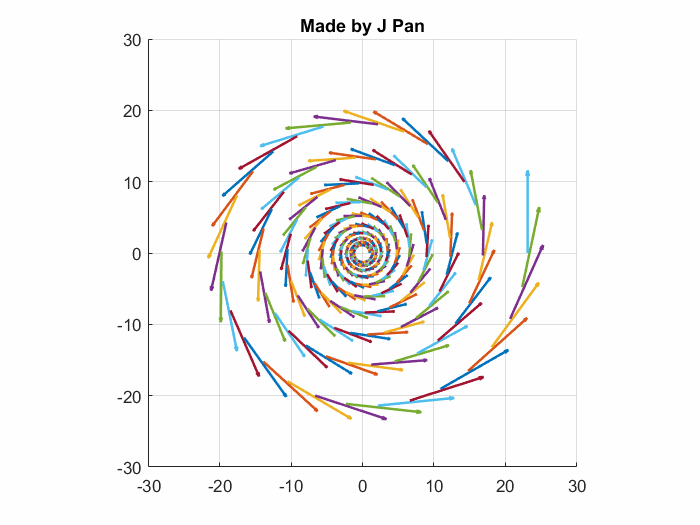
有了散度的概念做铺垫，旋度就好理解一点了，先说一下什么是环量：和通量类似，是指矢量沿着路径的闭合曲线积分，它能表示向量场围绕某一点的旋转程度。最常见的例子就是家里的洗衣机了：

环量的表达式为：

其中

为闭合曲线，

为曲线任意一点切线上单位矢量。

我们也很容易推出此点旋度，

点的旋度表达式为：

其中，

为封闭曲线

围成的区域面积，

为

的法向。要特别注意的是，既然是旋转，必然有一个旋转轴，也就说，旋度是一个

矢量。

2.3 梯度

梯度是这三个概念里面外面最熟悉的了，它表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大。简单点来说梯度能表达函数在某一点处变化最快的方向，既然是是方向，所以梯度也是一个矢量。表达式不复杂：

.

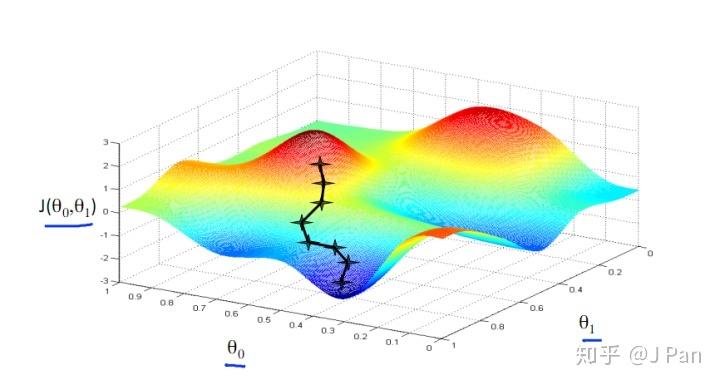
从我们朴素的直观感觉来说，梯度大能跟那些词联系起来呢？“险”？“陡”“居高临下”？——文雅一点，梯度代表着“势”。山势、地势，权势......老子说：“道生之，德畜之，物形之，势成之。”“势”是一个令人着迷的词，从古到今，人们一直都在使用它，但谁也说不清它。

2.4 什么是

算子

可能细心的童鞋已经注意到，在计算散度、旋度和梯度时，我们采用了一个符号：

。为什么要发明一个新符号呢？——前面我们说到散度是标量，旋度和梯度是矢量，而我们要描述的很多“场”，如电磁场，也是矢量场，因此在进行微积分运算的时候非常不方便，为此呢，我们采用一个矢量的运算符

（读作nabla）来计算，无它，就是图个方便而已。

nabla算符的定义式如下：

对于标量场，我们假设标量函数为：

；

对于矢量场，我们假设矢量函数为：

；

定义了

算子，很多事情就方便多了：

梯度：

与一个标量函数

乘积的结果；

散度：

与一个矢量函数

点积的结果；

旋度：

与一个矢量函数

叉积的结果；

---

三、如何理解麦克斯韦方程组

前面我们介绍了什么是散度、旋度及梯度，以及在数学上怎么表示，接下来就是见证奇迹的时刻了，先摆上大餐，微分形式的麦克斯韦方程组：

其中

表示电场，

表示磁场，

为真空电容率，

为真空磁导率，

是电荷密度，

是电流密度。眼尖的你可能已经发现，这尼玛就是

两个散度两个旋度啊。

3.1 散度说的是什么事

公式

、

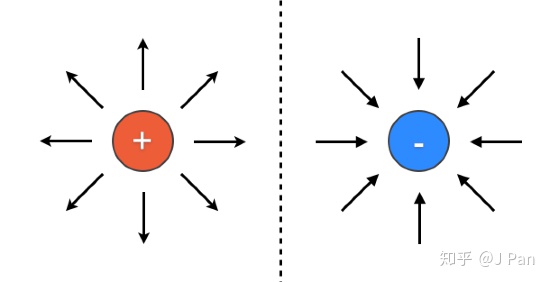
是关于散度的，公式

说，

电场的散度是电荷，而散度就是“源”，这说明什么呢？—— 电场是有源场，而且 电荷能增加电场的散度。啥叫有源场？——就是电场线可以有起点（源），或者终点，场线另一端可以延伸到无穷远处。当然，电场也可以是无源场，当

的时候。这条可以看成是对库伦定律和和高斯定律的抽象。

公式

说，

磁场的散度恒为零，这说明什么？——磁场永远是是 无源场，——就是磁力线没有起点，没有终点，永远是一个闭合状态，也就是说，在经典电磁理论里面，磁单极子是不存在的。

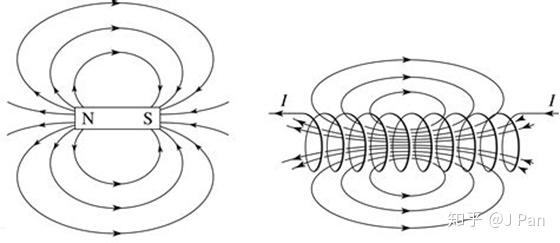
好了，既然电场有可能是无源场，磁场一直是无源场，那电场和磁场是怎么产生的呢？这就要看电磁场的另一个特性了——旋度。

3.2 旋度又说的什么事

公式

是说

磁场的变化率等于电场的旋度。可以从两个层面来看：（1）变化的磁场能产生电场，这是存在性问题；（2）变化的磁场产生什么样的电场——改变电场的旋度，粗略的说，可以产生环形电场，这条本质上说的是法拉第定律。

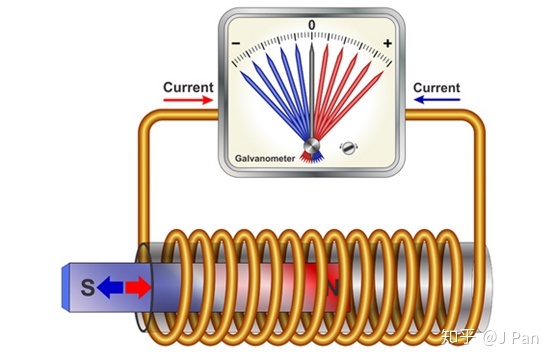
公式

内容就更丰富一些，主要说了两个事：（1）电流（运动的电荷）可以改变磁场的旋度；这就是安培定律嘛，也就是电流产生磁场。（2）变化的电场也能改变磁场的旋度，也就是安培-麦克斯韦定律。

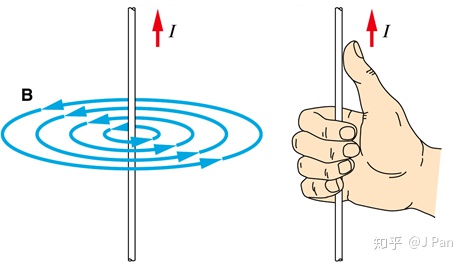
公式

、

说说明

变化的磁场能改变电场的旋度，变化的电场能改变磁场的旋度，旋度意味着什么？—— 意味着力线呈旋转或者螺旋状啊！

3.3 电磁波是个什么玩意

前面我我们们说到：电荷改变电场散度；电流改变磁场旋度；变化的电场或磁场也是改变旋度。而旋度意味着螺旋曲线，那是不是我们能观察的到呢？——能啊，电磁波不就是嘛！

想象在真空中，周围什么都没有，电荷密度和电流密度均为0，麦克斯韦方程组的微分形式就简化成了：

通过简单的推导，我们可以得出关于电场和磁场的两个方程：

这两个方程具有波动方程的形式，这说明了变化的电磁场以波的形态存在于自由空间中。其中

就是波传递的速度，

和

是关于真空的性质的两个常数，因此

也是一个常量，这个常量是和参考系无关的，数值大约是30万公里/秒。那么电磁场是如何传播的呢？下图是一个圆形极化的电场传播示意图，是不是看到了螺旋曲线的影子？（一般教材上的例子是线极化的电磁场，和这个图片不太一样，只是不同的解，感兴趣的可以去翻翻教材）。

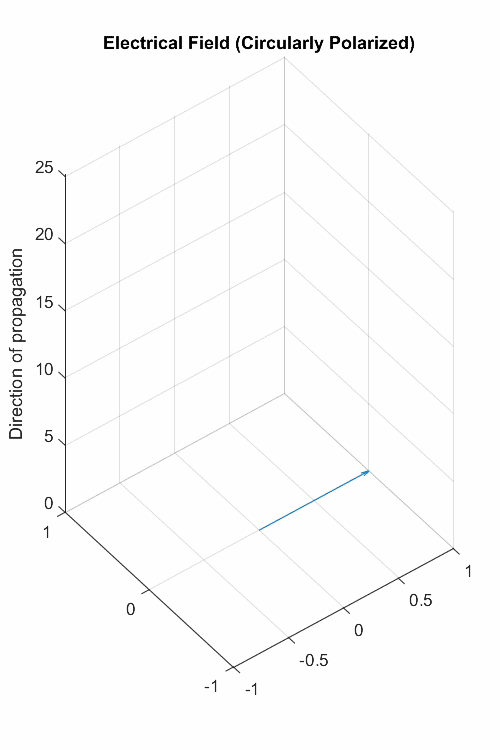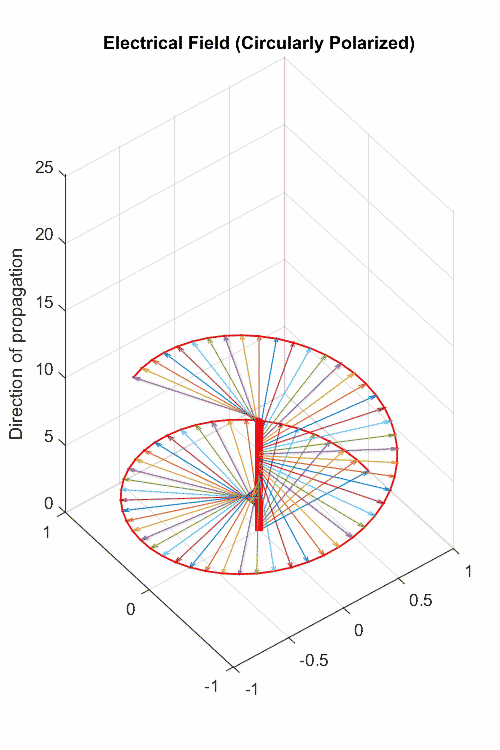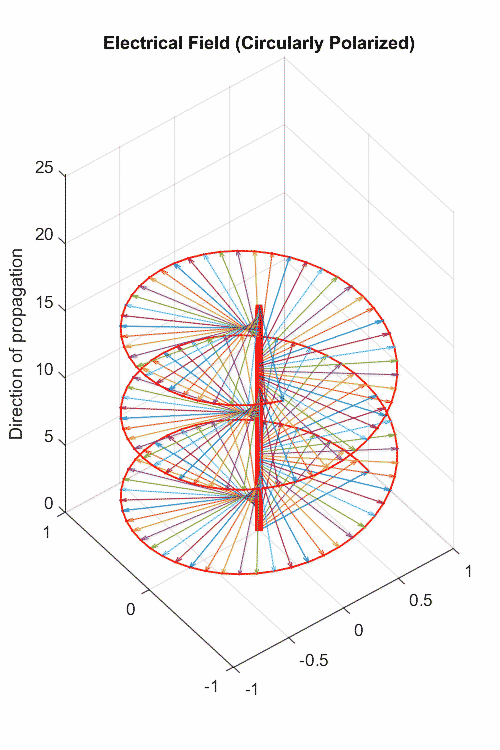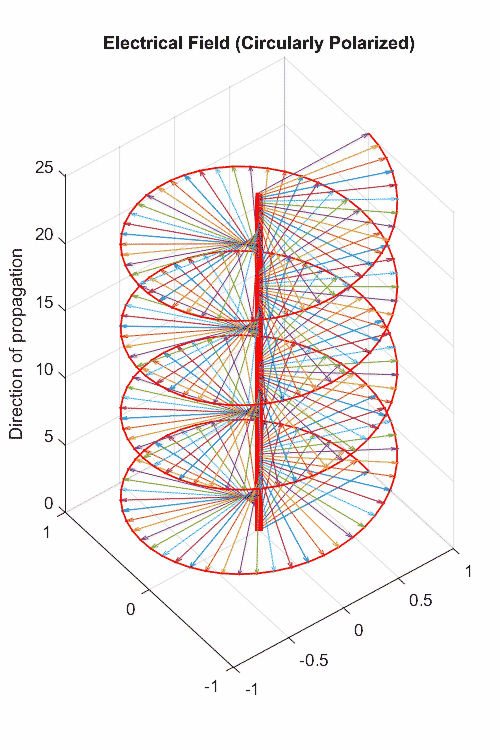
麦克斯韦方程组揭示了电场与磁场相互转化中产生的对称性优美，这种优美以现代数学形式，特别是在采用了nabla算子之后，得到了充分的表达。四个方程，两个用散度表示，两个用旋度表示，将复杂的电磁现象降低到了日常生活经验就能认知的程度：变化的磁场可以激发涡旋电场，变化的电场可以激发涡旋磁场，最终组成一个统一的电磁场。它所揭示出的电磁相互作用的完美统一，为物理学家树立了一种信念：物质的各种相互作用是不是应该在在更高层次上是统一的呢？

---

四、为什么要提梯度

前面只说散度和旋度，没说梯度的事啊，是不是电磁场里面就没梯度的事呢？别着急，这就要说呢。我们说，在真空中（无源情况下），麦克斯韦方程退化为:

该方程称之为波动方程，可以描述自然界中的各种的稳态波动现象，包括横波和纵波，例如声波、光波和水波，在声学，电磁学，和流体力学等领域应用广泛，其变种可以在量子力学和广义相对论中见到。

如果假定波在时间上是以某个频率做简谐振动的，

，则波动方程继续退化：

其中

,该方程称为简化波动方程，又叫

亥姆霍兹方程。

倘若在亥姆霍兹方程中，解的振动频率为零，也就是可以再去掉时间项，方程进一步退化为：

这就是大名鼎鼎的拉普拉斯方程，

就称之为拉普拉斯算子。拉普拉斯方程又称调和方程、位势方程，诸多自然现象都具有拉普拉斯方程的形式，如工程中常用的

传热方程。

前面说方的都是无源的情况，有源时，拉普拉斯方程变形为：

该方程称之为泊松方程，有热源时的固体热传导就符合泊松方程。

可能有些童鞋有点疑惑了，我们常见的无源传热方程长的是这个样子啊：

这俩货其实是一回事！只不过

是缩写形式，其原始的样子是

，聪明的你可能已经发现

就是标量函数

的

梯度，

就是标量函数

的

梯度的散度啊。我们前面说了，梯度代表着“势”，散度代表“来源”，那梯度的散度代表什么？—— 势的源头，该如何理解呢？还以传热为例：

即

说的是什么事？——空间中没有热源时的温度分布；

即

——在

处有一热源时空间的温度分布。

可见，如果用散度、旋度和梯度以及它们的组合来表示很多自然规律就简单的多了。这在本质上是我们发明了一个更复杂的概念来去描述一个相对复杂的现象，从而显得简单了。但前提是，你要花时间去消化这些概念，否则，如果只看公式，往往是只见迷雾，不见泰山。