简介:本压缩包深入探讨杨辉三角,一个源于南宋的数学结构,及其在多个领域中的应用。内容包括杨辉三角的推导过程、生成规则、性质、编程实现和扩展应用,旨在帮助学习者通过编程理解其组合数学原理,及其在预测数列模式等实际问题中的应用。 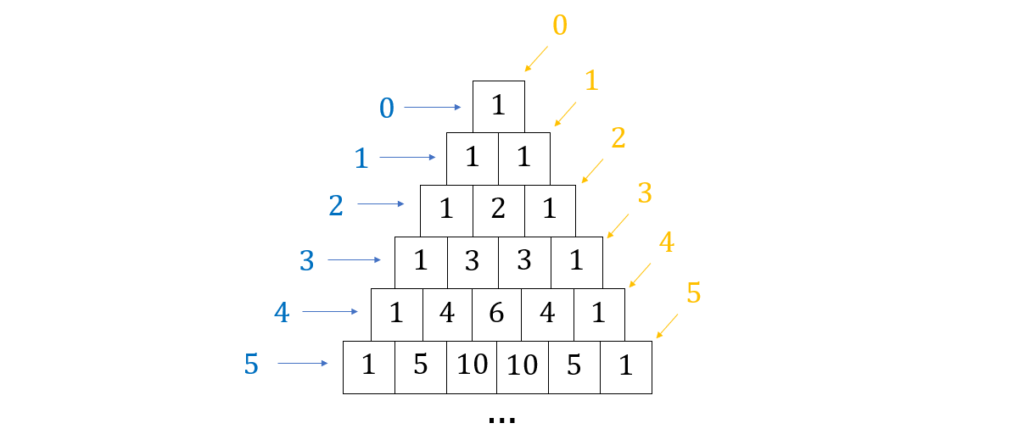
1. 杨辉三角基础概念
杨辉三角是数学中一个古老而著名的数列图形,具有丰富的历史背景和深远的应用价值。其形式上呈现为一个数字三角形,每个数是它左上方和右上方的数的和。这个三角形不仅在数学教育中占有重要位置,也是组合数学和概率论不可或缺的组成部分。杨辉三角的每一行对应于二项式展开式的系数,这些系数称为组合数,与诸多数学领域和实际应用紧密相关。
*
***
***
***
在本章,我们将探讨杨辉三角的历史渊源,挖掘其定义,并探究其与组合数学之间的内在联系。通过这一章的学习,读者将对杨辉三角有一个全面的了解,为后续章节中探讨杨辉三角的生成规则、性质、应用以及编程实现打下坚实的基础。
2. 杨辉三角生成规则
2.1 杨辉三角的数学定义和排列
2.1.1 杨辉三角的数学公式
杨辉三角,也被称为帕斯卡三角形,在数学上是一个将数字排列成一个三角形状的数组。在杨辉三角中,每个数是它左上方和右上方的数的和。在杨辉三角中,最外围的数全部是1,第二行的数也是1,而内部的数则为上方两个数的和。杨辉三角的数学公式可以表示为:
C(n, k) = C(n-1, k-1) + C(n-1, k)
这里,C(n, k)表示组合数,也就是从n个不同元素中,任取k(0 ≤ k ≤ n)个元素的组合数。这个公式直观地在杨辉三角中反映出来,每一项都可以通过上一行的左右两个数相加得到。
2.1.2 杨辉三角的组合数表示
组合数学中,杨辉三角的一行正好对应于自然数的幂次展开式中的系数。例如:
(1 + x)^n = C(n, 0) + C(n, 1)x + C(n, 2)x^2 + ... + C(n, n)x^n
其中,每个C(n, k)就是杨辉三角的第n+1行第k+1个数。因此,杨辉三角也可以看作是二项式系数的排列图,二项式定理中的系数是其直接体现。
2.2 杨辉三角的生成算法
2.2.1 递归算法
递归算法是最直观的生成杨辉三角的方法。我们可以定义递归函数来计算第n行的第k个数(C(n, k)),根据组合数学中的性质,可以得到递归关系:
C(n, k) = C(n-1, k-1) + C(n-1, k) (k > 0) C(n, 0) = C(n, n) = 1
递归实现简单,代码如下:
def comb(n, k):
if k == 0 or k == n:
return 1
return comb(n-1, k-1) + comb(n-1, k)
# 生成杨辉三角第n行
def pascal_triangle_row(n):
row = []
for k in range(n+1):
row.append(comb(n, k))
return row
# 生成整个杨辉三角
def generate_pascal_triangle(n):
triangle = []
for i in range(n):
triangle.append(pascal_triangle_row(i))
return triangle
2.2.2 迭代算法
由于递归算法存在重复计算的问题,导致效率低下,我们可以利用迭代的方式来优化。迭代算法通过存储上一行的结果,避免重复计算,提高效率。
迭代实现的代码如下:
def generate_pascal_triangle(n):
triangle = [[1]]
for i in range(1, n):
row = [1]
for j in range(1, i):
row.append(triangle[i-1][j-1] + triangle[i-1][j])
row.append(1)
triangle.append(row)
return triangle
2.2.3 空间优化方法
进一步优化空间,我们可以只保留杨辉三角的当前和上一行数据,而不是存储整个三角形。这样可以显著减少内存的占用。
空间优化的代码示例如下:
def generate_pascal_triangle(n):
prev_row = [1]
for i in range(n):
current_row = [1]
for j in range(1, i):
current_row.append(prev_row[j-1] + prev_row[j])
current_row.append(1)
print(current_row)
prev_row = current_row
2.2.4 代码逻辑的逐行解读
上述代码的逻辑是这样的:
- 初始化
prev_row为第一行的值[1]。 - 对于杨辉三角的每一行
i,初始化当前行current_row为[1]。 - 通过迭代计算
current_row中间的每个数,即current_row[j]为prev_row[j-1] + prev_row[j]。 - 每行的末尾添加一个
1,因为杨辉三角的每行最后一个数都是1。 - 打印当前行。
- 更新
prev_row为当前行current_row,为下一轮迭代做准备。
通过这种方式,我们可以有效地在有限的空间内生成任意行数的杨辉三角,并且每一步计算都是明确和高效的。
3. 杨辉三角性质与应用
3.1 杨辉三角的基本性质
3.1.1 对称性
杨辉三角最直观的性质之一就是它的对称性。当我们观察杨辉三角时,可以发现它的每一个数都关于中心线对称。换句话说,对于任意的第n行第k个数(n和k从0开始计数),都有一个对应的数在第n行的第(n-k)个位置上,这两个数相等。这一性质使得杨辉三角在视觉上呈现出独特的美感,也是其诸多性质中最为基础的一个。
对称性是杨辉三角的一个核心特征。通过对这一性质的深入理解,我们可以更加高效地计算杨辉三角中的数值。例如,在编程实现时,我们可以利用对称性质减少一半的计算量,提高算法的执行效率。
3.1.2 杨辉三角的数字特性
除了对称性之外,杨辉三角中每个数都是它上方两数之和,这是其最基本的递归性质。如果我们用P(n, k)表示杨辉三角第n行第k个数字,则有:
P(n, k) = P(n-1, k-1) + P(n-1, k)
这个递归关系在杨辉三角的生成算法中得到了广泛应用,特别是在动态规划优化时,它可以极大地减少重复计算,提高算法效率。
此外,杨辉三角中每行的首尾数字总是1,这也是一个重要的数字特性。这个性质对于程序中初始化数组非常有用,可以简化代码逻辑,减少边界检查。
3.2 杨辉三角在数学领域的应用
3.2.1 组合数学中的应用
杨辉三角在组合数学中的应用极为广泛。其中最为人所熟知的是,杨辉三角的每一行数字都可以与组合数直接对应。具体来说,杨辉三角第n行的第k个数(n和k从0开始计数)代表从n个不同元素中取出k个元素的组合数C(n, k)。这种对应关系,使得杨辉三角成为了组合数学中探讨各种组合问题的一个有力工具。
在教学和实际问题解决中,杨辉三角的这种性质常常用于直观展示组合数的递归关系,帮助学生和研究者深入理解组合数学的原理。
3.2.2 二项式系数的应用
杨辉三角与二项式系数有着紧密的联系。二项式定理表明,任何二项式的幂可以通过展开式中的二项式系数来表示。二项式系数的数值恰好就是杨辉三角中的数。这一性质使得杨辉三角在解决多项式展开和二项式定理相关问题时大放异彩。
例如,(a + b)^n 的展开式中各项的系数与第n+1行的杨辉三角数值一一对应。这一关系不仅对于代数学家来说非常重要,而且在物理学、工程学等领域中的应用也同样广泛。
由于杨辉三角与二项式系数的紧密联系,它也可以用来求解概率论中的问题。例如,二项分布的概率计算,就可以通过杨辉三角来简化。通过观察杨辉三角,我们可以快速得到一系列的二项式系数,这些系数与二项分布的概率质量函数直接相关。
3.3 杨辉三角在实际问题中的应用示例
示例:计算组合数 C(n, k)
假设我们要计算组合数C(5, 2),也就是从5个不同元素中取出2个元素的方式有多少种。根据杨辉三角的性质,我们可以直接观察第5行(即第6行,从0开始计数)来找到答案。
*
***
***
***
***
从上图可以看到,第5行的第2个数(从0开始计数)是3,因此C(5, 2) = 3。
示例:使用Python实现杨辉三角的对称性
下面是一个Python的简单实现,用来展示如何打印杨辉三角的对称性质:
def generate_pascal_triangle(num_rows):
triangle = [[1] * (i + 1) for i in range(num_rows)]
for n in range(2, num_rows):
for k in range(1, n):
triangle[n][k] = triangle[n-1][k-1] + triangle[n-1][k]
return triangle
def print_triangle(triangle):
width = len(" ".join(map(str, triangle[-1])))
for row in triangle:
print(" ".join(map(str, row)).center(width))
num_rows = 10
triangle = generate_pascal_triangle(num_rows)
print_triangle(triangle)
以上代码首先定义了一个函数 generate_pascal_triangle 用来生成杨辉三角,然后定义了另一个函数 print_triangle 来格式化输出杨辉三角,使其对称性更易于观察。运行这段代码,可以看到每行数字的对称排列。
以上是第三章的主要内容。在本章节中,我们深入探讨了杨辉三角的基本性质和在数学领域的应用。下一章节将带您进入杨辉三角的编程实现,探索如何将这些理论知识应用在实际的程序编写中。
4. 编程实现杨辉三角
杨辉三角不仅仅是一个数学上的有趣现象,它的实现更是一个经典的编程练习。在这一章节中,我们将探究如何使用不同的编程语言实现杨辉三角,并分享一些高级编程技巧来优化我们的实现。
4.1 初级编程语言实现杨辉三角
初级实现主要是为了让初学者理解杨辉三角的生成逻辑。接下来,我们将分别用Python、Java和C语言来实现杨辉三角。
4.1.1 使用Python实现
Python以其简洁的语法和强大的标准库,成为实现杨辉三角的理想选择。
def generate_pascal_triangle(rows):
triangle = []
for row_num in range(rows):
row = [1]
if triangle:
last_row = triangle[-1]
row.extend([sum(pair) for pair in zip(last_row, last_row[1:])])
row.append(1)
triangle.append(row)
return triangle
rows = 5
pascal_triangle = generate_pascal_triangle(rows)
for row in pascal_triangle:
print(row)
该代码块通过迭代的方式生成杨辉三角。函数 generate_pascal_triangle 接受一个参数 rows ,表示要生成的杨辉三角的行数。在这个函数中,我们首先初始化一个空的列表 triangle ,然后通过一个循环来构建每一行。对于每一行,我们首先添加数字1,接着,如果 triangle 不为空,我们使用 zip 和 sum 函数计算中间的元素,并在行尾再添加一个1。
4.1.2 使用Java实现
Java实现通常比Python的代码更繁琐一些,但是能够得到更好的性能表现。
import java.util.ArrayList;
import java.util.List;
public class PascalTriangle {
public static List<List<Integer>> generate(int numRows) {
List<List<Integer>> triangle = new ArrayList<List<Integer>>();
if (numRows <= 0) {
return triangle;
}
for (int row = 0; row < numRows; row++) {
List<Integer> newRow = new ArrayList<Integer>();
for (int col = 0; col <= row; col++) {
if (col == 0 || col == row) {
newRow.add(1);
} else {
newRow.add(triangle.get(row - 1).get(col - 1) + triangle.get(row - 1).get(col));
}
}
triangle.add(newRow);
}
return triangle;
}
public static void main(String[] args) {
int numRows = 5;
List<List<Integer>> pascalTriangle = generate(numRows);
for (List<Integer> row : pascalTriangle) {
System.out.println(row);
}
}
}
这段Java代码与Python实现的逻辑相似,但使用了Java的集合框架来存储每一行。对于每一行,我们创建一个新的ArrayList来存放行内的值。在Java中,我们使用 triangle.get(row - 1).get(col - 1) + triangle.get(row - 1).get(col) 来计算中间的元素,因为Java不支持直接解压列表,我们需要分别访问两个元素。
4.1.3 使用C语言实现
C语言实现则更接近底层,有助于理解内存管理和指针的使用。
#include <stdio.h>
void printPascalTriangle(int n) {
int arr[n][n]; // 创建一个二维数组来存储杨辉三角的每一行
// 初始化杨辉三角的第一行
for (int line = 0; line < n; line++) {
// 每一行的第一个和最后一个数字是1,其余为0
for (int i = 0; i <= line; i++) {
if (line == i || i == 0)
arr[line][i] = 1;
else // 其他位置的数字是上一行的两个数字之和
arr[line][i] = arr[line - 1][i - 1] + arr[line - 1][i];
printf("%d ", arr[line][i]);
}
printf("\n");
}
}
int main() {
int n = 5;
printPascalTriangle(n);
return 0;
}
在C语言版本中,我们使用一个二维数组 arr 来存储杨辉三角的每一行,其中 n 是我们想生成的杨辉三角的行数。在初始化循环中,我们逐行逐个元素地生成三角形的值。每一行的第一个和最后一个元素被初始化为1,其余的元素则通过加上上一行的相邻两个元素来计算得出。
4.2 高级编程技巧优化杨辉三角
随着我们对杨辉三角有了基础的理解,现在我们探索一些更高级的编程技巧来进一步优化我们的实现。
4.2.1 动态规划优化
动态规划是解决杨辉三角生成效率问题的一个常用方法,它存储了之前计算的值,避免了重复计算。
def optimized_pascal_triangle(n):
triangle = [[1], [1, 1]]
if n <= 2:
return triangle[:n]
for i in range(2, n):
row = [1]
last_row = triangle[-1]
for j in range(1, i):
row.append(last_row[j - 1] + last_row[j])
row.append(1)
triangle.append(row)
return triangle
# 使用动态规划方法生成杨辉三角的前5行
triangle = optimized_pascal_triangle(5)
for row in triangle:
print(row)
这段代码通过构建一个二维数组 triangle 来存储当前已经计算出的行。在构建每一行的过程中,我们只计算并存储新行的元素,而不再重新计算前一行的元素。这样可以显著减少计算量,提高效率。
4.2.2 大数处理和边界条件
在处理杨辉三角的时候,我们可能会遇到数值非常大的情况,这时需要考虑大数处理和边界条件。
import math
def large_number_pascal_triangle(n):
triangle = [[***b(i, j) for j in range(i + 1)] for i in range(n)]
return triangle
# 使用大数处理方法生成杨辉三角的前5行
triangle = large_number_pascal_triangle(5)
for row in triangle:
print(row)
在处理大数的情况下,使用Python内置的 ***b 函数可以方便地计算组合数,即杨辉三角中的每一个数字。该函数会处理很大的数,并返回精确结果,避免了整数溢出的问题。
请注意,在Java和C语言中,处理大数可能需要自定义方法来模拟高精度的数学运算,这将增加实现的复杂性。
在这些章节中,我们通过不同编程语言实现了杨辉三角的基本算法,并探讨了一些高级优化技巧。在下一章节中,我们将深入探讨杨辉三角在概率论与计算机科学中的广泛应用。
5. 杨辉三角在概率论与计算机科学中的应用
5.1 杨辉三角与概率论的交汇
5.1.1 二项式定理与概率计算
二项式定理是概率论中的一个重要工具,它描述了在一系列独立的、具有两个可能结果的试验中,成功次数恰好为k的概率。二项式定理可以表示为:
(a + b)^n = Σ (n choose k) * a^(n-k) * b^k
其中, (n choose k) 就是杨辉三角中的第n行第k个数,它代表了在n次试验中恰好有k次成功的组合数。杨辉三角提供了一种直观的、几何上的表示方法,使得计算这些组合数变得非常简单。
5.1.2 杨辉三角在随机过程中的应用
杨辉三角同样适用于分析随机过程,如马尔可夫链和随机漫步。例如,在一个简单的随机漫步问题中,我们可以使用杨辉三角来表示从起点到达某一特定点的路径数。在n步随机漫步中,每个点的到达次数是对应杨辉三角的第n行数字。
5.2 杨辉三角在计算机科学中的角色
5.2.1 数据结构与算法设计
杨辉三角可以被看作是一个非常特殊的二叉树结构,其中每个节点的值等于它的左子节点和右子节点的值之和。这种结构在计算机科学中的数据结构设计中有着广泛的应用,尤其是在实现堆结构、霍夫曼编码等算法时。
5.2.2 杨辉三角在图论和搜索算法中的应用
在图论中,杨辉三角的结构可以用来表示某些特殊类型的图,如完全二部图的完美匹配数量。同时,在搜索算法中,杨辉三角可以用来优化路径查找问题。例如,在一个n层的二叉搜索树中,从根节点到叶子节点的路径数对应于杨辉三角的第n行数字。
在设计搜索算法时,了解杨辉三角可以帮助我们更好地预测算法的复杂度。例如,如果一个算法是递归的,并且每一步都重复了前一步的过程,那么它的性能可能与杨辉三角的某个特性相关。
杨辉三角不仅是数学游戏和理论问题中的工具,它实际上在现代计算机科学和概率论中扮演着重要角色。通过分析杨辉三角的性质,我们可以对许多复杂问题有更深刻的理解,并且能够设计出更高效的算法来解决这些问题。
简介:本压缩包深入探讨杨辉三角,一个源于南宋的数学结构,及其在多个领域中的应用。内容包括杨辉三角的推导过程、生成规则、性质、编程实现和扩展应用,旨在帮助学习者通过编程理解其组合数学原理,及其在预测数列模式等实际问题中的应用。
























 953
953

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








