简介:本项目旨在MATLAB中探索和实现地球重力随高度变化的模拟。通过理解重力的基本概念和应用牛顿万有引力定律,我们将使用MATLAB的强大数学工具来计算和可视化这一物理现象。项目的具体步骤包括导入相关数据、定义重力计算函数、进行计算、可视化结果、分析趋势,并考虑额外因素进行优化和扩展。该实践将加深对重力变化规律和MATLAB编程技巧的理解。 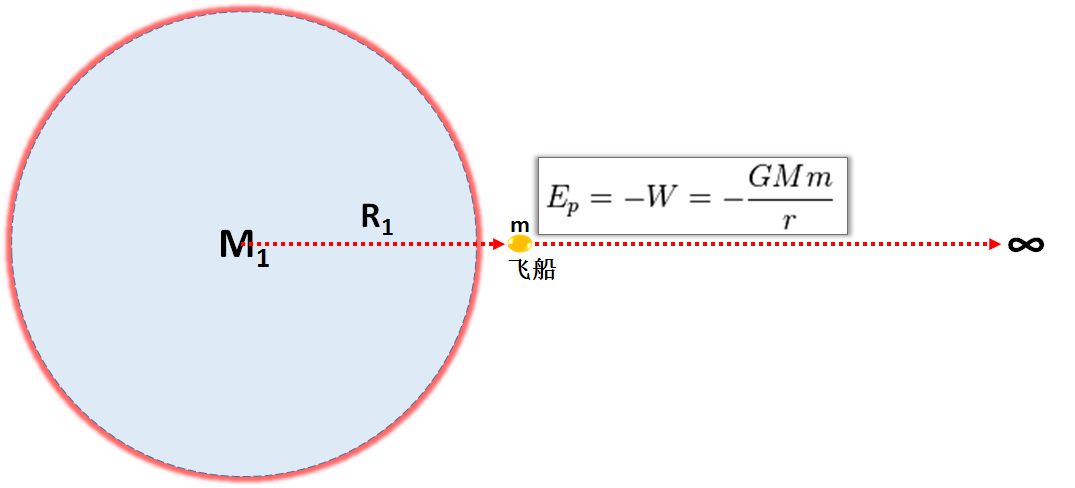
1. MATLAB中物理计算和数值模拟的应用
1.1 物理计算在MATLAB中的角色
MATLAB软件不仅在工程领域广受欢迎,在物理计算和数值模拟方面也占据了重要位置。利用其强大的数学计算能力和丰富的函数库,MATLAB成为进行复杂物理问题求解的首选工具。这不仅仅是因为它可以处理线性、非线性等方程,更在于它提供的可视化功能可以直观展示计算结果,辅助进行科学研究。
1.2 数值模拟的基本步骤
在MATLAB中进行物理计算和数值模拟,一般遵循以下几个基本步骤:首先,定义问题的物理方程和边界条件;然后,选择适当的数值方法进行离散化处理;接下来,编写相应的MATLAB脚本进行求解;最后,分析和可视化模拟结果以验证模型和理解物理现象。这个过程往往需要反复迭代,直至获得满意的结果。
% 示例:绘制简单的二次方程 y = x^2 的图像
x = -10:0.1:10; % 定义x的取值范围
y = x.^2; % 计算对应的y值
plot(x, y); % 绘制图像
title('y = x^2'); % 添加标题
xlabel('x'); % x轴标签
ylabel('y'); % y轴标签
以上代码块演示了如何在MATLAB中绘制一个基础的函数图像,这是进行物理计算和数值模拟的重要基础。通过这种方式,复杂的物理问题可以借助图形化工具被更直观地理解和分析。
2. 地球重力与高度关系的探索
2.1 地球重力的基本概念和理论
2.1.1 地球重力的定义和起源
地球重力是地球对物体的吸引力,其根源在于地球的质量所产生的重力场。根据牛顿万有引力定律,任何两个物体之间都存在吸引力,这个力与两个物体的质量成正比,与它们之间距离的平方成反比。地球重力可以视为地球对质量单位的吸引力。
地球的重力场可以简化为一个均匀的向心场,在地球表面上任一点,重力的方向为该点的法线方向,大小则由地球的质量和半径决定。这个力使得地球上的物体具有重量,并影响各种自然现象,如潮汐、物体下落等。
2.1.2 地球重力场的特性
地球重力场的特性由地球的质量分布决定。地球是一个不规则的椭球体,其质量分布并非完全均匀,因此地球重力场也存在不均匀性。这种不均匀性导致地球的重力加速度在不同位置有所不同。
重力场的这种不均匀性在测量中表现为重力异常,可以通过测量地球表面不同位置的重力值,来绘制等重力线图,即重力异常图。这不仅可以用于探索地球内部的物质分布,还可以用于导航和地球物理研究。
2.2 地球重力与高度的关系
2.2.1 高度对重力影响的理论分析
随着高度的增加,物体距离地球中心的距离变大,根据牛顿万有引力定律,物体受到的重力会逐渐减小。实际上,地球并不是一个完美的球体,而是赤道稍微隆起的椭球体,这就意味着随着高度增加,地球的曲率以及重力场的方向也会发生变化。
此外,地球的重力场还受到其他因素的影响,如地壳密度的变化、潮汐力等。因此,高度对重力的影响并不是简单的反比关系,需要借助更精确的物理模型来描述。
2.2.2 不同高度下重力的计算模型
为了计算不同高度下的地球重力,科学家和工程师已经开发了多种计算模型。其中,国际重力公式(IGF)就是一个常用的简化模型,它可以用来估算特定海拔高度下的重力加速度。
一个更为精确的方法是使用地球重力模型(Earth Gravity Model,EGM),这种模型通常是基于大量重力测量数据的球谐系数,能够提供全球范围内各个高度的重力加速度估计。EGM模型可以用来生成全球重力场的详细地图,对于测量、制图、导航和地球科学领域都有重要意义。
接下来的章节将详细探讨如何利用MATLAB来实现和分析这些模型。
3. 牛顿万有引力定律的应用
牛顿万有引力定律是物理学史上的一项伟大成就,它不仅揭示了天体之间引力的普遍性,还为后续的科学革命奠定了基础。牛顿在1687年发表了《自然哲学的数学原理》,其中提出了这个定律。它描述了两个物体之间引力的大小与它们的质量成正比,并与它们之间距离的平方成反比。本章节将详细探讨该定律在现代科学研究中的应用,特别是在MATLAB软件中的实现与应用实例。
3.1 牛顿万有引力定律概述
3.1.1 定律的提出和数学表达
牛顿万有引力定律的提出,是基于开普勒行星运动定律的研究。牛顿通过数学归纳和实验验证,提出了引力定律的数学表达式:
[ F = G \frac{m_1 m_2}{r^2} ]
这里的 ( F ) 表示两个物体间的引力大小,( G ) 是引力常数,( m_1 ) 和 ( m_2 ) 分别是两个物体的质量,( r ) 是两个物体质心之间的距离。这个公式说明,任何两个物体都会相互吸引,而且这种引力与它们的质量成正比,与它们之间的距离的平方成反比。
3.1.2 定律在地球重力研究中的应用
地球重力的研究是牛顿万有引力定律的一个典型应用领域。根据牛顿引力定律,地球表面任意物体的重力可以表示为:
[ F = G \frac{m M_{\text{Earth}}}{R_{\text{Earth}}^2} ]
其中 ( m ) 是物体的质量,( M_{\text{Earth}} ) 是地球的质量,( R_{\text{Earth}} ) 是地球的半径。通过这个公式,科学家可以计算出地球表面不同位置的重力加速度,以及如何受到地球自转等因素的影响。
3.2 牛顿万有引力定律在MATLAB中的实现
在MATLAB中实现牛顿万有引力定律,可以用来模拟不同质量物体之间的引力作用,并分析其运动轨迹。这不仅有利于理解引力定律的理论基础,还能够对天体力学、卫星轨道设计等实际问题提供数值解。
3.2.1 MATLAB中的引力计算模型
以下是一个简单的MATLAB模型,用于计算两个物体之间的引力。假设我们有质量为 ( m_1 ) 和 ( m_2 ) 的两个物体,它们之间的距离为 ( r ),计算它们之间的引力大小。
function F = gravitational_force(m1, m2, r)
G = 6.67430e-11; % 引力常数,单位 m^3 kg^-1 s^-2
F = G * (m1 * m2) / r^2;
end
这个函数接受三个参数:两个物体的质量 ( m_1 ) 和 ( m_2 ),以及它们之间的距离 ( r ),并返回引力的大小 ( F )。
3.2.2 实例演示和结果分析
让我们看一个具体的例子。假设质量为 ( m_1 = 5.972 \times 10^{24} ) kg(即地球质量)和 ( m_2 = 70 ) kg(即一个人的质量),他们之间的距离为 ( r = 6.371 \times 10^6 ) m(地球半径)。
m1 = 5.972e24; % 地球质量,单位 kg
m2 = 70; % 人质量,单位 kg
r = 6.371e6; % 地球半径,单位 m
F = gravitational_force(m1, m2, r);
fprintf('两物体之间的引力大小为: %e Newton\n', F);
执行这段代码,我们可以得到一个地球表面的人所受的重力为 ( 6.866 \times 10^2 ) 牛顿。
通过这个简单的模型,我们可以探索更多的物理现象,如改变物体质量或距离对引力的影响,以及它如何在不同的天体间起作用。MATLAB的强大计算功能使得在理论和应用层面上的研究成为可能。
以上就是对牛顿万有引力定律在MATLAB中应用的概述和一个简单模型的实现。在后续章节中,我们将深入探讨地球重力与高度的关系,以及如何使用MATLAB进行更复杂的物理模拟和数据分析。
4. MATLAB数据导入和函数定义
4.1 MATLAB数据导入方法
4.1.1 从文件中导入数据
MATLAB提供了多种方式来导入不同格式的数据文件,这使得它在处理来自各种源的数据时变得非常灵活。使用 load 函数可以导入 .mat 文件,而 readmatrix 或者 readtable 函数可以用于导入CSV或文本文件。
在导入文件数据时,理解文件的结构至关重要。例如,CSV文件可能包含分隔符,例如逗号、制表符或空格,这需要在导入时指定。
% 从CSV文件中导入数据到矩阵
dataMatrix = readmatrix('data.csv', 'Delimiter', ',');
% 从文本文件中导入数据到表格
dataTable = readtable('data.txt', 'Delimiter', '\t');
4.1.2 通过接口获取数据
MATLAB提供了强大的接口功能,允许开发者从数据库、网络服务和其他外部资源中直接获取数据。使用 database 函数可以连接到支持ODBC或JDBC的数据库。此外,可以使用 webread 、 webservice 和 websave 等函数来调用RESTful Web服务和解析JSON或XML数据。
% 连接到数据库
conn = database('DatabaseName', 'Username', 'Password');
% 从数据库中查询数据
dataFromDB = exec(conn, 'SELECT * FROM myTable');
% 断开数据库连接
close(conn);
4.1.3 从其他程序导入数据
MATLAB与外部程序的数据交换可通过多种方式实现,例如使用 ActiveX 控件与支持COM的应用程序交互,或通过 mex 文件接口与C或C++代码共享数据。
4.2 MATLAB函数的定义和使用
4.2.1 自定义函数的创建和调用
在MATLAB中,函数是一段可以执行特定任务并可被重复调用的代码。自定义函数通过编写一个具有 .m 扩展名的文件来定义,并保存在MATLAB的路径或当前工作目录中。
函数文件由一个函数声明行开始,后面跟着函数体,其中可以包含变量、语句、控制流语句和输出参数。
% 定义一个计算矩形面积的函数
function area = calculateArea(length, width)
% 计算矩形的面积
area = length * width;
end
% 调用函数
rectArea = calculateArea(10, 5);
4.2.2 内置函数的应用和优化
MATLAB内置了大量优化过的数学和工程函数,开发者可以利用这些函数提高工作效率。在使用内置函数时,需要了解它们的语法、参数以及如何正确地传递数据。
对于某些特定的任务,可能需要对内置函数进行参数优化以提高性能,这涉及到函数的调用方式和参数选择。例如,使用 fft 函数进行快速傅里叶变换时,可以调整数据块的大小以优化执行速度和内存使用。
% 对信号进行FFT变换
signal = rand(1, 1024); % 示例信号
fftSignal = fft(signal);
% 优化FFT参数
n = 2^nextpow2(length(signal)); % 下一个2的幂
fftSignalOptimized = fft(signal, n);
4.2.3 函数的封装和封装性优化
封装是面向对象编程中的一个基本概念,意味着将代码和数据封装在一个单独的单元内。在MATLAB中,函数封装可以提高代码的可维护性和可重用性。使用私有文件和子函数可以对函数进行封装,从而保护数据和实现细节不被外部访问。
封装后的函数可以进一步优化,例如,通过限制函数作用域和参数传递的开销,减少全局变量的使用,以提高函数的执行效率。
% 使用私有函数封装算法
function result = complexOperation(x, y)
privateResult = privateFunction(x);
result = privateResult + y;
end
% 私有函数只对complexOperation可见
function value = privateFunction(a)
value = a^2; % 简单运算
end
通过以上的章节内容,我们深入探讨了MATLAB数据导入和函数定义的方法和技巧。在第四章的内容中,我们不仅学习了如何从各种数据源导入数据到MATLAB环境,还了解了如何通过自定义函数和封装来优化数据处理流程。在下一章节,我们将探索物理计算中重力加速度随高度变化的计算方法,并展示如何在MATLAB中实现这些计算模型。
5. 重力加速度随高度变化的计算方法
5.1 重力加速度变化的理论基础
5.1.1 重力加速度与高度的理论关系
重力加速度是描述物体因地球重力作用而获得的加速度大小,通常标记为g。在物理学中,g并不是一个常量,它会随着地球表面的不同位置和高度而发生变化。根据牛顿万有引力定律,重力加速度与物体到地球中心的距离的平方成反比。这一点可以从以下公式中得到体现:
[ g = G \frac{M}{r^2} ]
其中,G是万有引力常数,M是地球的质量,r是物体到地球中心的距离。从这个公式我们可以看出,当物体离地球表面更远时,也就是高度h增加时,重力加速度g会减小。
5.1.2 影响重力加速度变化的因素分析
除了高度外,地球的自转也会对重力加速度产生影响。地球自转导致地球在赤道处膨胀,因此赤道半径略大于极半径。此外,地球并非完美的球体,而是扁球体,这种形状导致了不同纬度的重力加速度存在差异。
地球内部的密度不均匀性也是导致重力加速度变化的一个因素。山脉、洞穴、矿藏等地质构造均会影响地表重力场。
5.2 MATLAB中的重力加速度计算模型
5.2.1 建立计算模型的步骤
在MATLAB中建立重力加速度随高度变化的计算模型,需要遵循以下步骤:
- 定义地球的基本参数,如质量、半径、万有引力常数等。
- 选择一种地球重力场模型,如WGS-84。
- 编写一个函数来计算给定高度处的重力加速度。
- 考虑地球自转和其他非对称因素对重力加速度的影响。
- 对模型进行测试,使用已知的数据点验证模型的准确性。
- 提供用户输入和输出接口,以便于用户使用该模型。
5.2.2 实现模型计算的MATLAB脚本编写
% 定义地球的基本参数
G = 6.67430e-11; % 万有引力常数,单位 m^3 kg^-1 s^-2
M = 5.972e24; % 地球质量,单位 kg
Re = 6371000; % 地球平均半径,单位 m
% 计算重力加速度的函数
function g = calcGravityAcceleration(h)
% 如果高度h未提供,则默认为地面高度
if nargin < 1
h = 0;
end
% 计算到地心的总半径
r = Re + h;
% 计算重力加速度
g = G * M / r^2;
end
% 使用示例
h = 10000; % 高度为10000米
g = calcGravityAcceleration(h);
fprintf('在高度 %d 米处的重力加速度约为 %f m/s^2\n', h, g);
在上述代码中,我们定义了地球的基本物理参数,并创建了一个函数 calcGravityAcceleration 用于计算指定高度上的重力加速度。函数接受一个参数 h ,它代表相对于地面的高度,如果未提供,函数默认高度为0,即地面。计算中使用了牛顿万有引力定律,根据高度计算重力加速度。
需要注意的是,此模型是一个简化模型,它没有考虑如地球自转等因素。若要提高计算的准确性,还需进一步增加计算复杂度,加入其他影响因素。
6. MATLAB绘图功能和数据分析
MATLAB不仅仅是一个数值计算工具,它还具备强大的图形处理和数据分析能力,使得数据的可视化和理解变得直观和便捷。在处理复杂的数据集时,绘图和数据分析是关键步骤,能够帮助我们快速识别模式、趋势和异常值。本章将深入探讨MATLAB绘图功能的应用,以及其在数据分析方面提供的工具和方法。
6.1 MATLAB绘图功能的应用
6.1.1 二维绘图的基本用法
MATLAB中的二维绘图是最基本且广泛使用的图形表达方式。例如,绘制正弦波函数曲线可以使用 plot 函数。下面是一个简单的示例代码:
% 定义一个从0到2π的向量作为x轴数据点
x = linspace(0, 2*pi, 100);
% 计算对应的正弦函数值作为y轴数据点
y = sin(x);
% 绘制曲线
figure;
plot(x, y);
% 添加标题和坐标轴标签
title('正弦波函数');
xlabel('角度');
ylabel('sin(角度)');
执行上述代码将生成一个标准的二维曲线图。
6.1.2 三维绘图和数据可视化技巧
三维绘图在某些情况下可以提供更丰富的视觉效果和更深入的数据洞察。MATLAB提供了多种三维绘图功能,比如 plot3 、 mesh 、 surf 等。下面是使用 surf 函数绘制三维曲面的示例:
[X, Y] = meshgrid(-5:0.25:5, -5:0.25:5);
Z = sin(sqrt(X.^2 + Y.^2));
figure;
surf(X, Y, Z);
shading interp; % 平滑着色
colormap jet; % 设置色彩映射
colorbar; % 显示颜色条
title('三维正弦曲面');
xlabel('X轴');
ylabel('Y轴');
zlabel('sin(sqrt(X^2 + Y^2))');
这段代码将生成一个三维正弦曲面的可视化图像,其中 shading interp 命令用于使曲面平滑着色, colormap jet 设置色彩映射, colorbar 为图像添加了颜色条。
6.2 MATLAB数据分析方法
6.2.1 数据处理和分析工具箱介绍
MATLAB提供了多个内置的数据分析工具箱,例如统计和机器学习工具箱(Statistics and Machine Learning Toolbox)、图像处理工具箱(Image Processing Toolbox)等。这些工具箱包含多种函数和方法,用于数据分析、图像处理、信号分析等复杂任务。例如,使用 fit 函数可以对数据进行拟合分析:
% 生成一些带有噪声的正弦数据
x = linspace(0, 2*pi, 50);
y = sin(x) + randn(size(x)) * 0.5;
% 使用高斯函数进行拟合
[p, s] = fit(x', y', 'gauss');
% 绘制原始数据和拟合曲线
figure;
plot(x, y, 'b*', x, p(x), 'r-');
legend('原始数据', '拟合曲线');
title('高斯拟合示例');
上述代码使用高斯函数对带有噪声的数据进行了拟合。
6.2.2 实例分析:从数据到洞察的全过程
在现实世界的数据分析任务中,我们往往需要执行从数据清洗、预处理到模式识别和结果解释的全过程。以下是一个完整的数据分析案例:
-
数据导入 :首先,我们需要导入数据到MATLAB。这可以通过
readtable函数或importdata函数实现。 -
数据清洗 :使用
rmmissing函数去除数据中的缺失值,使用unique函数去除重复的记录。 -
统计分析 :利用
mean、median、std等函数计算数据集的基本统计量。 -
可视化 :通过绘制箱形图、直方图等来可视化数据的分布情况。
-
模式识别 :使用聚类算法如
kmeans对数据集进行无监督学习,发现潜在的模式。 -
结果解释 :根据聚类结果,解释各聚类的特征和意义,为决策提供依据。
通过上述过程,我们可以从杂乱的数据中提取有用信息,进而得到有价值的数据洞察。
在本章中,我们学习了MATLAB的绘图功能和数据分析方法。从绘制基本的二维曲线到复杂的三维曲面,从简单的统计数据计算到复杂的数据模式识别,MATLAB提供了一整套强大的工具来帮助我们有效地进行数据的可视化和分析。无论是进行物理计算、数值模拟,还是处理地球重力数据、建立物理模型,MATLAB的这些功能都能够大幅度提升工作效率和结果的准确性。
简介:本项目旨在MATLAB中探索和实现地球重力随高度变化的模拟。通过理解重力的基本概念和应用牛顿万有引力定律,我们将使用MATLAB的强大数学工具来计算和可视化这一物理现象。项目的具体步骤包括导入相关数据、定义重力计算函数、进行计算、可视化结果、分析趋势,并考虑额外因素进行优化和扩展。该实践将加深对重力变化规律和MATLAB编程技巧的理解。
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








