(动态规划整理)

最新推荐文章于 2024-11-04 23:39:13 发布

weixin_33725270

最新推荐文章于 2024-11-04 23:39:13 发布

阅读量99

点赞数

文章标签：数据结构与算法

这一篇博客以一些OJ上的题目为载体。整理一下动态规划(DP)的应用

一、利用动态规划来解决最长公共子序列(LCS)问题

1、NYOJ 36 最长公共子序列

1）这一道题。要理解清楚状态转移方程

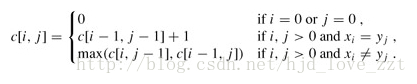
2）回溯法求LCS的过程

3）对于get()函数的理解。仅仅要你看过《算法导论》这本书，就会非常清楚为什么这样写了

4）在求LCS的时候事实上还是基于遍历的思想

/*
 * NY36_2.cpp
 *
 *  Created on: 2014年5月25日
 *      Author: pc
 */

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>


using namespace std;

const int maxn = 1005;

int c[maxn][maxn];
//返回c[i][j]。c[i][j]表示字符串a的前i个字符和字符串b的前j个字符的最长公共子序列的长度
int get(int i,int j){
	if(i >= 0 && j >= 0){
		return c[i][j];
	}

	return 0;
}
int main(){
	int t;
	scanf("%d",&t);

	while(t--){
		char a[maxn];
		char b[maxn];

		memset(c,0,sizeof(c));

		scanf("%s%s",&a,&b);

//		gets(a);//用这样的方法会出错...我也不知道为什么
//		gets(b);

		int n = strlen(a);
		int m = strlen(b);

		int i,j;
		for(i = 0 ; i < n ; ++i){
			for(j = 0 ; j < m ; ++j){
				if(a[i] == b[j]){
					c[i][j] = get(i-1,j-1) + 1;
				}else{
					c[i][j] = max(get(i-1,j),get(i,j-1));
				}
			}
		}

		printf("%d\n",c[n-1][m-1]);//这里之所以使用c[n-1][m-1],是由于c[n-1][m-1]已经是状态转移方程中的右下角的那一个格子了
	}

	return 0;
}

2、HDOJ 1159

思想：差点儿是一模一样的题目。除了输入的处理逻辑不一样外没有什么不一样的

/*
 * HDOJ_1159.cpp
 *
 *  Created on: 2014年5月25日
 *      Author: pc
 */


#include <iostream>
#include <cstdio>

using namespace std;


const int maxn = 1005;

int c[maxn][maxn];
int get(int i,int j){
	if(i >= 0 && j >= 0){
		return c[i][j];
	}

	return 0;
}

int main(){
	char a[maxn];
	char b[maxn];

	while(scanf("%s %s",&a,&b)!=EOF){
		memset(c,0,sizeof(c));

		int n = strlen(a);
		int m = strlen(b);

		int i,j;
		for(i = 0 ; i < n ; ++i){
			for(j = 0 ; j < m ; ++j){
				if(a[i] == b[j]){
					c[i][j] = get(i-1,j-1) + 1;
				}else{
					c[i][j] = max(get(i-1,j),get(i,j-1));
				}
			}
		}

		printf("%d\n",c[n-1][m-1]);
	}

	return 0;
}

3、POJ 1458（和上面的那道题一模一样）

二、利用动态规划(DP)来解决最长上升子序列问题(LIS)

最长上升子序列问题的两中常见的算法：

1）O(n^2): 我们依次遍历整个序列。每一次求出从第一个数到当前这个数的最长上升子序列，直至遍历到最后一个数字为止。然后再取dp数组里最大的那个即为整个序列的最长上升子序列。

我们用dp[i]来存放序列1-i的最长上升子序列的长度。那么dp[i]=max(dp[j])+1,(j∈[1, i-1]); 显然dp[1]=1,我们从i=2開始遍历后面的元素即可。

2）O(nlgn)：在从前i-1个数中找出满足a[j]<a[i]（1<=j<i）条件的最大的L[j]的时间复杂度为O(n)，这里採用二分查找的方法对它进行优化，使其复杂度降为O(nlog ⁿ )。

增设一个m[]数组，m[x]存放长度为x的最长上升子序列的最小末尾数。例：m[3] = 17表示长度为3的最长上升子序列的最小末尾数为17。

由于子序列是上升的，所以m数组中的元素有一个性质，当x<y时。m[x]<m[y]。利用这个性质来使用二分查找。

设m数组所存储的最长上升子序列的长度为k。当前计算的数为第i个假设a[i]>m[k]。则m[++k]=a[i]。否则在m[1~k]内二分查找小于（等于）a[i]的最大值的位置p，m[p]=a[i]。

Ex：举例：原序列为1，5，8，3。6。7
栈为1。5。8，此时读到3，则用3替换5。得到栈中元素为1，3，8，再读6，用6替换8，得到1。3。6，再读7，得到终于栈为1，3，6。7 。最长递增子序列为长度4。

这时候。事实上m[]就是一个记录了当中一个最长上升子序列的数组.(a[]为原始序列)

总结的说。另外一种方法就是增设了一个m[]数组用来记录当中的一种最长上升子序列。m[i]=a表示长度为i的最长上升子序列中的末尾数是a。若当前计算到的数a[i]>m[k],则m[++k] = a[i]。否则在1~i中寻找一个合适的位置在a[i]

1、山东理工大学OJ 1299 最长上升子序列

题目分析：

这道题是求最长上升子序列的长度。

1)方法一：

/*
 * SD_1299.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;

/**
 * 该函数用于求最长上升子序列
 */
int LIS(int a[],int n){

	int dp[n+1];

	int i;
	int j;

	for(i = 1 ; i <= n ; ++i){//白努力求每个索引的最长上升子序列的长度
		int m = 0;

		for(j = 1 ; j < i ; ++j){//去到当前索引i的的最长上升子序列的长度
			if(dp[j] > m && a[i] > a[j]){
				m = dp[j];
			}
		}

		dp[i] = m+1;
	}

	int ans = 0;
	for(i = 1 ; i <= n ; ++i){//其最长上升子序列的长度
		if(dp[i] > ans){
			ans = dp[i];
		}
	}

	return ans;
}

int main(){
	int n;
	while(scanf("%d",&n)!=EOF){
		int a[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%d",&a[i]);
		}

		int result = LIS(a,n);

		printf("%d\n",result);
	}

	return 0;
}

方法二：

/*
 * SD_1299_Nlgn.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;


int binary_search(int a[],int n,int t){
	int low = 1;
	int high = n;

	while(low <= high){
		int mid = (low+high)/2;

		if(t == a[mid]){
			return mid;
		}else if(t < a[mid]){
			high = mid-1;
		}else{
			low = mid+1;
		}
	}

	return low;

}


int LIS_BINARY(int a[],int m[] ,int n){
	int maxLen = 1;
	m[maxLen] = a[1];

	int i;
	for(i = 2 ; i <= n ; ++i){
		if(m[maxLen] < a[i]){
			m[++maxLen] = a[i];
		}else{
			int p = binary_search(m,maxLen,a[i]);
			m[p] = a[i];
		}
	}



	return maxLen;
}

int main(){
	int n;
	while(scanf("%d",&n)!=EOF){
		int a[n+1];
		int m[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%d",&a[i]);
		}

		int result = LIS_BINARY(a,m,n);

		printf("%d\n",result);
	}

	return 0;
}

2、POJ 2533

题目分析：

这一道题和上面那一道题是一样的

3、WIKIOI 1576

题目分析：

这道题还是求最长上升子序列

方法一：

/*
 * WIKIOI_1576.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;

int LIS(int a[],int n){
	int dp[n+1];

	int i;
	int j;
	for(i = 1 ; i <= n ; ++i){
		int m = 0;

		for(j = 1 ; j < i ; ++j){
			if(dp[j] > m && a[j] < a[i]){
				m = dp[j];
			}
		}

		dp[i] = m + 1;
	}

	int ans = 0;
	for(i = 1 ; i <= n ; ++i){
		if(dp[i] > ans){
			ans = dp[i];
		}
	}

	return ans;
}

int main(){
	int n;
	while(scanf("%d",&n)!=EOF){
		int a[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%d",&a[i]);
		}

		int result = LIS(a,n);

		printf("%d\n",result);
	}

	return 0;
}

方法二：

/*
 * WIKIOI_1576_NLGN.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;


int binary_search(int a[],int n, int t){
	int low = 1;
	int high = n;

	while(low <= high){
		int mid = (low+high)/2;

		if(t == a[mid]){
			return mid;
		}else if(t > a[mid]){
			low = mid+1;
		}else{
			high = mid-1;
		}
	}

	return low;
}


int LIS_Binary(int a[],int m[],int n){
	int maxLen = 1;
	m[maxLen] = a[1];

	int i;
	for(i = 2 ; i <= n ; ++i){
		if(m[maxLen] < a[i]){
			m[++maxLen] = a[i];
		}else{
			int p = binary_search(m,maxLen,a[i]);
			m[p] = a[i];
		}
	}

	return maxLen;
}


int main(){
	int n;
	while(scanf("%d",&n)!=EOF){
		int a[n+1];
		int m[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%d",&a[i]);
		}

		int result = LIS_Binary(a,m,n);

		printf("%d\n",result);
	}

	return 0;
}

4、九度OJ 1533 最长上升子序列

题目分析：这道题使用O(n^2)的算法会TLE,因此用法二来解决

#include <iostream>
#include <cstdio>

using namespace std;


/**
 * 二分查找
 */
int binary_search(int a[],int n, int t){
	int low = 1;
	int high = n;

	while(low <= high){
		int mid = (low+high)/2;

		if(t == a[mid]){
			return mid;//假设找到了返回找到的位置
		}else if(t > a[mid]){
			low = mid+1;
		}else{
			high = mid-1;
		}
	}

	return low;
}


int LIS_Binary(int a[],int m[],int n){
	int maxLen = 1;
	m[maxLen] = a[1];

	int i;
	for(i = 2 ; i <= n ; ++i){
		if(m[maxLen] < a[i]){
			m[++maxLen] = a[i];
		}else{
			int p = binary_search(m,maxLen,a[i]);
			m[p] = a[i];
		}
	}

	return maxLen;
}


int main(){
	int n;
	while(scanf("%d",&n)!=EOF){
		int a[n+1];
		int m[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%d",&a[i]);
		}

		int result = LIS_Binary(a,m,n);

		printf("%d\n",result);
	}

	return 0;
}

5、POJ 1887 Testing the CATCHE

题目分析：求最长非升子序列。

这一道题与前面最大的不同就在于：求最长非升子序列。前面都是求最长上升子序列。这里用到了一个技巧：将数据保存进a[]之前。先将数据取一下反。另外还须要注意一下的就是这道题中的数据的输入的方式。其它的事实上也就没有什么了

1)方法一：

/*
 * POJ_1887.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */


#include <iostream>
#include <cstdio>

using namespace std;

const int maxn = 1000000;
int a[maxn];

int LIS(int a[],int n){
	int i;

	int dp[n+1];

	for(i = 1 ; i <= n ; ++i){
		int m = 0;

		int j;
		for(j = 1 ; j < i ; ++j){
			if(dp[j] > m && a[j] < a[i]){
				m = dp[j];
			}
		}

		dp[i] = m+1;
	}

	int ans = 0;
	for(i = 1 ; i <= n ; ++i){
		if(dp[i] > ans){
			ans = dp[i];
		}
	}

	return ans;
}

int main(){
	int t = 0;

	while(++t){
		int temp;

		int n = 0;
		while(true){
			scanf("%d",&temp);
			if(temp == -1){
				break;
			}

			a[++n] = -temp;
		}

		if(n == 0){
			return 0;
		}

		int result = LIS(a,n);

		if(t != 1){
			printf("\n");
		}

		printf("Test #%d:\n",t);
		printf("  maximum possible interceptions: %d\n",result);
	}

	return 0;
}

2）方法二：

/*
 * POJ_1887.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */


#include <iostream>
#include <cstdio>

using namespace std;

const int maxn = 100000;

int a[maxn];
int m[maxn];

int binary_search(int a[],int n,int t){
	int low = 1;
	int high = n;

	while(low <= high){
		int mid = (low+high)/2;

		if(t == a[mid]){
			return mid;
		}else if(t > a[mid]){
			low = mid+1;
		}else{
			high = mid-1;
		}
	}

	return low;
}


int LIS_Binary(int a[],int m[],int n){
	int maxLen = 1;
	m[maxLen] = a[1];

	int i;
	for(i = 2 ; i <= n ; ++i){
		if(m[maxLen] < a[i]){
			m[++maxLen] = a[i];
		}else{
			int p = binary_search(m,maxLen,a[i]);
			m[p] = a[i];
		}
	}

	return maxLen;
}


int main(){
	int t = 0;
	while(++t){

	    int n = 0;
		int temp;
		while(true){//特别要注意这道题的输入数据时候的方式
			scanf("%d",&temp);

			if(temp == -1){
				break;
			}

			a[++n] = -temp;//求最长不升子序列问题的技巧...
		}

		if(n == 0){
			return 0;
		}


		if(t != 1){
			printf("\n");
		}

		int result = LIS_Binary(a,m,n);


		printf("Test #%d:\n",t);
		printf("  maximum possible interceptions: %d\n",result);
	}

	return 0;
}

6、POJ 1631

题目与分析：

这道题仅仅能使用O(nlgn)算法来解决。

/*
 * POJ_1631_nlgn.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;

int binary_search(int a[],int n,int t){
	int low = 1;
	int high = n;

	while(low <= high){
		int mid = (low+high)/2;

		if(t == a[mid]){
			return mid;
		}else if(t > a[mid]){
			low = mid+1;
		}else{
			high = mid-1;
		}
	}

	return low;
}


int LIS_Binary(int a[],int m[],int n){
	int maxLen = 1;
	m[maxLen] = a[1];

	int i;
	for(i = 1 ; i <= n ; ++i){
		if(m[maxLen] < a[i]){
			m[++maxLen] = a[i];
		}else{
			int p = binary_search(m,maxLen,a[i]);
			m[p] = a[i];
		}
	}

	return maxLen;
}


int main(){
	int t;
	scanf("%d",&t);

	while(t--){
		int n;
		scanf("%d",&n);

		int a[n+1];
		int m[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%d",&a[i]);
		}

		int result = LIS_Binary(a,m,n);

		printf("%d\n",result);
	}

	return 0;
}

7、POJ 1609 Tiling Up Blocks

题目与分析：

这是一道二维的最长上升子序列(LIS)的问题.

Ex:从一个样例来看题意
(4,2),(2,4),(3,3),(1,1),(5,5)
那么3是怎么出来的呢(1,1)->(2,4)->(5,5)

方法一：

/*
 * POJ_1609.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

struct Num {
	int a;
	int b;
};

int cmp(const void* a, const void* b) {
	Num c = (*(Num*) a);
	Num d = (*(Num*) b);

	if (c.a != d.a) {
		return c.a - d.a;
	} else {
		return c.b - d.b;
	}
}

int LIS(Num nums[], int n) {
	int dp[n + 1];

	int i;
	for (i = 1; i <= n; ++i) {
		int m = 0;

		int j;
		for (j = 1; j < i; ++j) {
			if (dp[j] > m && nums[j].a <= nums[i].a && nums[j].b <= nums[i].b) {
				m = dp[j];
			}
		}

		dp[i] = m + 1;
	}

	int ans = 0;
	for (i = 1; i <= n; ++i) {
		if (dp[i] > ans) {
			ans = dp[i];
		}
	}

	return ans;
}

int main() {
	int n;
	while (scanf("%d", &n) != EOF) {
		if (n == 0) {
			printf("*\n");
			return 0;
		}

		Num nums[n + 1];
		int i;
		for (i = 1; i <= n; ++i) {
			scanf("%d%d", &nums[i].a, &nums[i].b);
		}

		qsort(nums + 1, n, sizeof(nums[1]), cmp);

		int result = LIS(nums, n);

		printf("%d\n", result);
	}

	return 0;
}

8、NYOJ 79 拦截导弹

题目与分析：

这道题与POJ 1887是一样的。都是求最长非升子序列。

仅仅是数据的输入方式有点不同而已。

1）方法一

/*
 * NJOJ_79.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */


#include <iostream>
#include <cstdio>

using namespace std;

int LIS(int a[],int n){
	int dp[n+1];

	int i;
	for(i = 1 ; i <= n ; ++i){
		int m = 0;

		int j;
		for(j = 1 ; j < i ; ++j){
			if(dp[j] > m && a[j] < a[i]){
				m = dp[j];
			}
		}

		dp[i] = m+1;
	}

	int ans = 0;
	for(i = 1 ; i <= n ; ++i){
		if(dp[i] > ans){
			ans = dp[i];
		}
	}

	return ans;
}


int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		int n;
		scanf("%d",&n);
		int a[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			int temp;
			scanf("%d",&temp);
			a[i] = -temp;
		}

		int result = LIS(a,n);

		printf("%d\n",result);
	}

	return 0;
}

2）方法二

/*
 * NY_79_NLGN.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */


#include <iostream>
#include <cstdio>

using namespace std;


int binary_search(int a[],int n,int t){
	int low = 1;
	int high = n;

	while(low <= high){
		int mid = (low+high)/2;

		if(t == a[mid]){
			return mid;
		}else if(t > a[mid]){
			low = mid+1;
		}else{
			high = mid-1;
		}
	}

	return low;
}

int LIS_Binary(int a[],int m[],int n){
	int maxLen = 1;
	m[maxLen] = a[1];

	int i;
	for(i = 1 ; i <= n ; ++i){
		if(m[maxLen] < a[i]){
			m[++maxLen] = a[i];
		}else{
			int p = binary_search(m,maxLen,a[i]);
			m[p] = a[i];
		}
	}

	return maxLen;
}

int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		int n;
		scanf("%d",&n);

		int a[n+1];
		int m[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			int temp;
			scanf("%d",&temp);
			a[i] = -temp;
		}

		int result = LIS_Binary(a,m,n);

		printf("%d\n",result);
	}

	return 0;
}

9、NYOJ 17 单调递增子序列

题目与分析：

这道题与前面的题的不同之处就在于。原始序列由数字序列变成了字符序列。

在这样的情况下，仅仅须要办函数的參数改成char类型的即可了。

算法的思想还是一样的。。。

题目与分析：

1）方法一

/*
 * NY_17.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;

int LIS(string a,int n){
	int dp[n+1];

	int i;
	for(i = 0 ; i < n ; ++i){
		int m = 0;

		int j;
		for(j = 0 ; j < i ; ++j){
			if(dp[j] > m && a[j] < a[i]){
				m = dp[j];
			}
		}

		dp[i] = m+1;
	}

	int ans = 0;
	for(i = 0 ; i < n ; ++i){
		if(dp[i] > ans){
			ans = dp[i];
		}
	}

	return ans;
}

int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		string a;
		cin >> a;//曾经的经验,这里假设使用gets(a)会有一些问题...
		int n = a.length();

		int result = LIS(a,n);

		printf("%d\n",result);

	}

	return 0;
}

2）方法二：

/*
 * NY_17_nlgn.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;


int binary_search(string a,int n,char t){
	int low = 0;
	int high = n-1;
	while(low <= high){
		int mid = (low+high)/2;

		if(t == a[mid]){
			return mid;
		}else if(t > a[mid]){
			low = mid+1;
		}else{
			high = mid-1;
		}
	}

	return low;
}


int LIS_Binary(string a,string m,int n){
	int maxLen = 0;
	m[maxLen] = a[0];

	int i;
	for(i = 0 ; i < n ; ++i){

		if(m[maxLen] < a[i]){
			m[++maxLen] = a[i];
		}else{
			int p = binary_search(m,maxLen,a[i]);
			m[p] = a[i];
		}
	}

	return maxLen;
}

int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		string a;
		string m;

		cin >> a;
		int n = a.length();

		int result = LIS_Binary(a,m,n);

		printf("%d\n",result+1);
	}

	return 0;
}

10、NY 214

题目分析：这道题还是求最长上升子序列的长度。由于本体的数据量比較大，用方法一的话会TLE,所以本体仅仅能用法二。

方法二：

/*
 * NY_214.cpp
 *
 *  Created on: 2014年6月4日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;


int binary_search(int a[],int n,int t){
	int low = 1;
	int high = n;
	while(low <= high){
		int mid = (low+high)/2;

		if(t == a[mid]){
			return mid;
		}else if(t > a[mid]){
			low = mid+1;
		}else{
			high = mid-1;
		}
	}

	return low;
}

int LIS_Binary(int a[],int m[],int n){
	int maxLen = 1;
	m[maxLen] = a[1];

	int i;
	for(i = 1 ; i <= n ; ++i){

		if(m[maxLen] < a[i]){
			m[++maxLen] = a[i];
		}else{
			int p = binary_search(m,maxLen,a[i]);
			m[p] = a[i];
		}
	}

	return maxLen;
}

int main(){
	int n;
	while(scanf("%d",&n)!=EOF){
		int a[n+1];
		int m[n+1];

		int i;
		for(i = 1 ; i <= n ; ++i){
			scanf("%d",&a[i]);
		}

		int result = LIS_Binary(a,m,n);

		printf("%d\n",result);
	}

	return 0;
}