函数平移口诀_函数图像的平移规律，你凌乱吗？

大家知道吗？数学学科这一称谓已经成为历史，数学已经更名为一门科学！既然是科学，那就离不开实验。今天要和大家交流的函数图像平移规律，就是在数学实验中得以发现的。下面的数学实验都是在一款著名数学软件“几何画板”里进行的，且听本人慢慢道来！

我们都知道函数是描述两个变量x、y的对应关系的，对定义域内的每一个x值，都有且仅有一个y值与之对应。下列的实验就是对"在自变量x上加或减一个常数m(m>0)，即x±m"与“在函数y上加或减一个常数m(m>0)，即y±m”进行的探索研究。

一、一次函数图像的平移实验

1、“x+m”或“y+m”(m>0)对函数图像的影响

图中实验一是分别论证“x+m”与“y+m”(m>0)对图像的影响。m=3，当仅是x+3时，从图中比较红线与白线的位置，我们可发现“x+3”导致白线向左平移了3个单位得到红线；当仅是y+3时，从图中比较蓝线与白线的位置，我们可发现“y+3”导致白线向下平移了3个单位得到蓝线；当同时有“x+m”与“y+m”时，新学同学容易感到迷惑，大家可以试一试这么看：黄线可以看做是“将白线向左平移3个单位得到红线，再将红线向下平移3个单位得到”，或者看做“将白线向下平移3个单位得到蓝线，再将蓝线向左平移三个单位得到”。

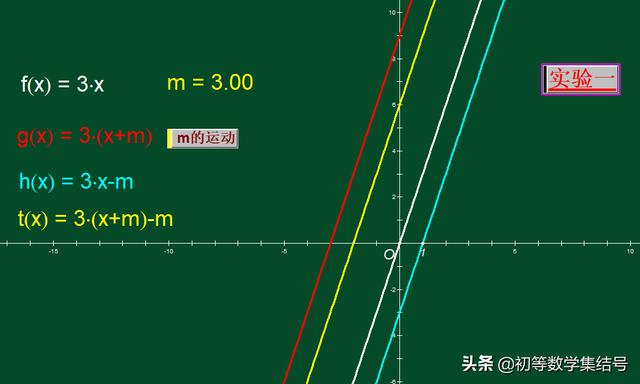
源函数y=3x，实验分别论证“x+m”与"y+m"对图像的影响(m>0)

2、“x-m”或“y-m”(m>0)对函数图像的影响

图中实验二是分别论证“x-m”与“y-m”(m>0)对图像的影响。m=4，当仅是x-4时，从图中比较红线与白线的位置，我们可发现“x-4”导致白线向右平移了4个单位得到红线；当仅是y-4时，从图中比较蓝线与白线的位置，我们可发现“y-4”导致白线向上平移了4个单位得到蓝线；当同时有“x-m”与“y-m”时，新学同学容易感到迷惑，大家可以试一试这么看：黄线可以看做是“将白线向右平移4个单位得到红线，再将红线向上平移4个单位得到”，或者看做“将白线向上平移4个单位得到蓝线，再将蓝线向右平移4个单位得到”。

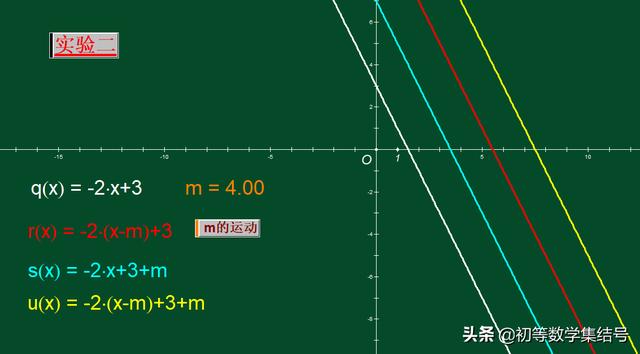
源函数y=-2x+3，实验分别论证“x-m”与"y-m"对图像的影响(m>0)

3、函数图像平移中的等价效果现象

如图，这是“x+m”与“y+m”(m>0)对图像的影响。m=3，当仅是x+3时，从图中比较红线与白线的位置，我们可发现“x+3”导致白线向左平移了3个单位得到红线。聪明细心的同学会发现：图中红线相对于白线的位置也可以看做“将白线向上平移9个单位得到红线”，这是怎么回事呢？静静一想，你会发现：原来是等价效果！具体原因：函数解析式y=3(x+3)，去括号后等价为y=3x+9；当仅是y+3时，从图中比较蓝线与白线的位置，我们可发现“y+3”导致白线向下平移了3个单位得到蓝线。同样聪明细心的你会发现：图中蓝线相对于白线的位置也可以看做“将白线向右平移1个单位得到蓝线”，这是怎么回事呢？静静一想，你会发现：原来是等价效果！具体原因：函数解析式y=3x-3，添括号后等价为y=3(x-1)。

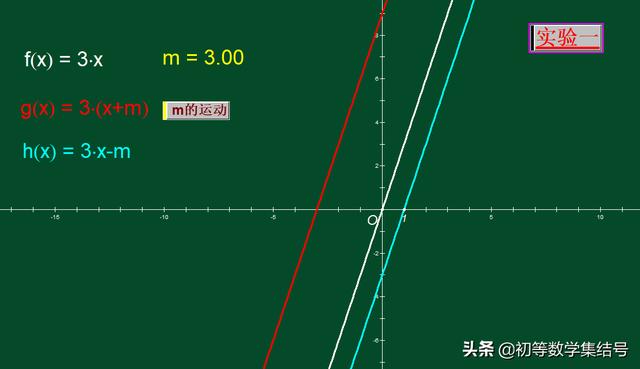
二、实验结论

1、“x+m”(m>0)对图像产生的效果是：将原函数图像向左平移m个单位；

“x-m”(m>0)对图像产生的效果是：将原函数图像向右平移m个单位。

2、“y+m”(m>0)对图像产生的效果是：将原函数图像向下平移m个单位；

“y-m”(m>0)对图像产生的效果是：将原函数图像向上平移m个单位。

大家都知道，经过论证或实验获得真理后，接下来紧接着要做的重要事情是主动加工这些真理以期实现良好的记忆储存知识，本人称这个过程为“打上自己的烙印”。下面就介绍一下本人在这个实验结论上的“打上自己烙印”。思考分析，图像的平移不外就两种方向“水平方向与竖直方向”。水平方向里“左为负、右为正”，竖直方向里“下为负、上为正”。再将平移方向上的正负与“+、-”对应，顿时就得到发现：无论是“x±m”还是“y±m”,'+'对应的平移方向是负方向，‘-’对应的平移方向是正方向。

故本人对函数图像平移规律的记忆口诀形成了，她是：正负颠倒。将所学知识或真理打上自己的烙印，往往会形成自己独特的记忆要领，这也是自己学习过程中一件十分成功、快乐的事情！聪明好学的你，可以行动起来试一试将知识“打上自己的烙印”。

三、实验结论在二次函数的体现

同学们平时的相关练习题已经相当多了，本人这里就不增加额外负担啦！但为了巩固实验结论，接下来请大家跟我到“一元二次函数的图像平移”里再次论证“函数图像平移规律”。

1、水平方向上的平移

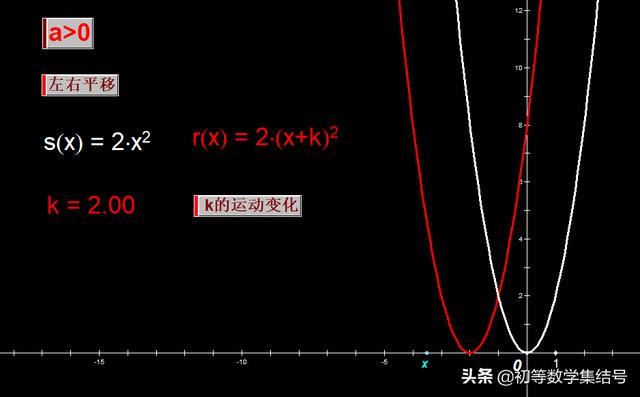
“x+2”对函数图像的平移效果

2、竖直方向上的平移

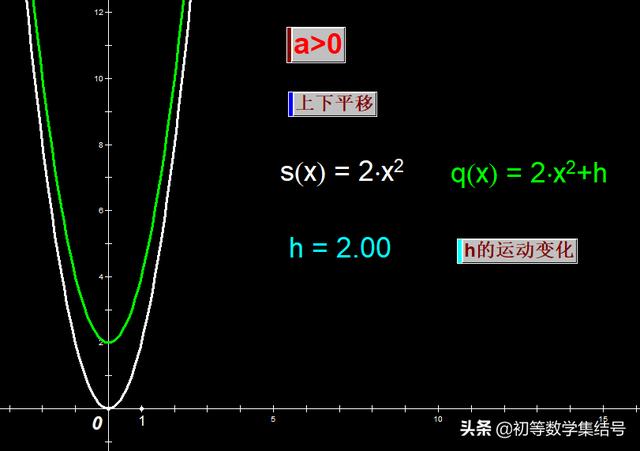
“y-2”对函数图像平移的效果

3、水平与竖直方向的复合平移

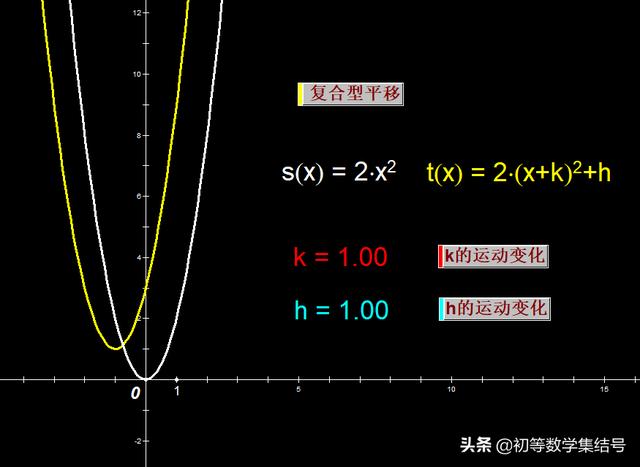
“x+1”与“y-1”复合对函数图像平移的效果

从函数图像平移规律可知，黄色抛物线是由白色抛物线向左平移1个单位再向上平移1个单位所得，也可以看做“由白色抛物线向上平移1个单位再向左平移一个单位所得”。

欢迎大家阅读此文学习，最后留下一个思考供大家讨论：一次函数图像的平移中的“等价效果现象”，在一元二次函数图像的平移中还继续存在吗？