逻辑回归与正则化

1、逻辑回归

其实逻辑回归是从线性回归演化而来的（逻辑回归虽然有回归两字，但其实是做分类任务）。就举吴恩达的肿瘤预测为例，假如肿瘤是这样分布的，横轴为肿瘤大小，纵轴为是否是肿瘤（0或1），那么将样本点画在图上

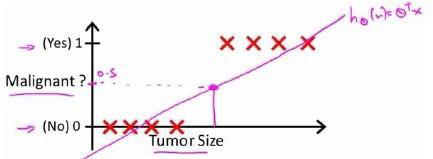
当时，预测。
当时，预测。
这里有一点我要讲明白，根据函数图像，为1的点几乎都在函数图形上方，为0的点几乎都在线下方。时，预测指的是点向x轴做垂线与图像相交的地方大于0.5为1，其他的一样。
上面这种看上去不错，但如果有一个异常点的肿瘤大小特别大（所以建模时去除异常点多重要），那么影响函数图像变为蓝色的直线：

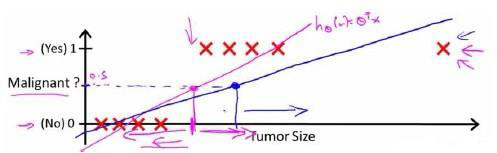
可以看出大于0.5为1的话，那么就有两个为1的归为不是肿瘤，导致分类错误。
所以引入sigmoid函数：，而，得。损失函数也可以用平方差损失函数，但是的图像是一个非凸函数，影响梯度下降寻找最小值。
我们重新定义逻辑回归的损失函数为：，其中

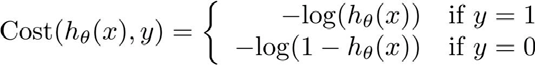
和之间的关系如图，横轴是，纵轴是，每个图像都有一个定值1或0（重要！！）：

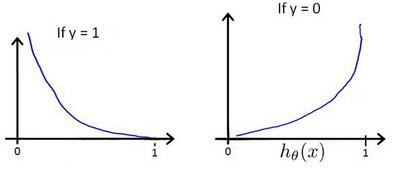
这样构建的函数的特点是：当实际上且时，误差为0，当且时，误差随着的变小而变大；当时类似。
将构建的简化如下：

代入得到：

即：
然后，我们使用梯度下降来求:

求导如下：

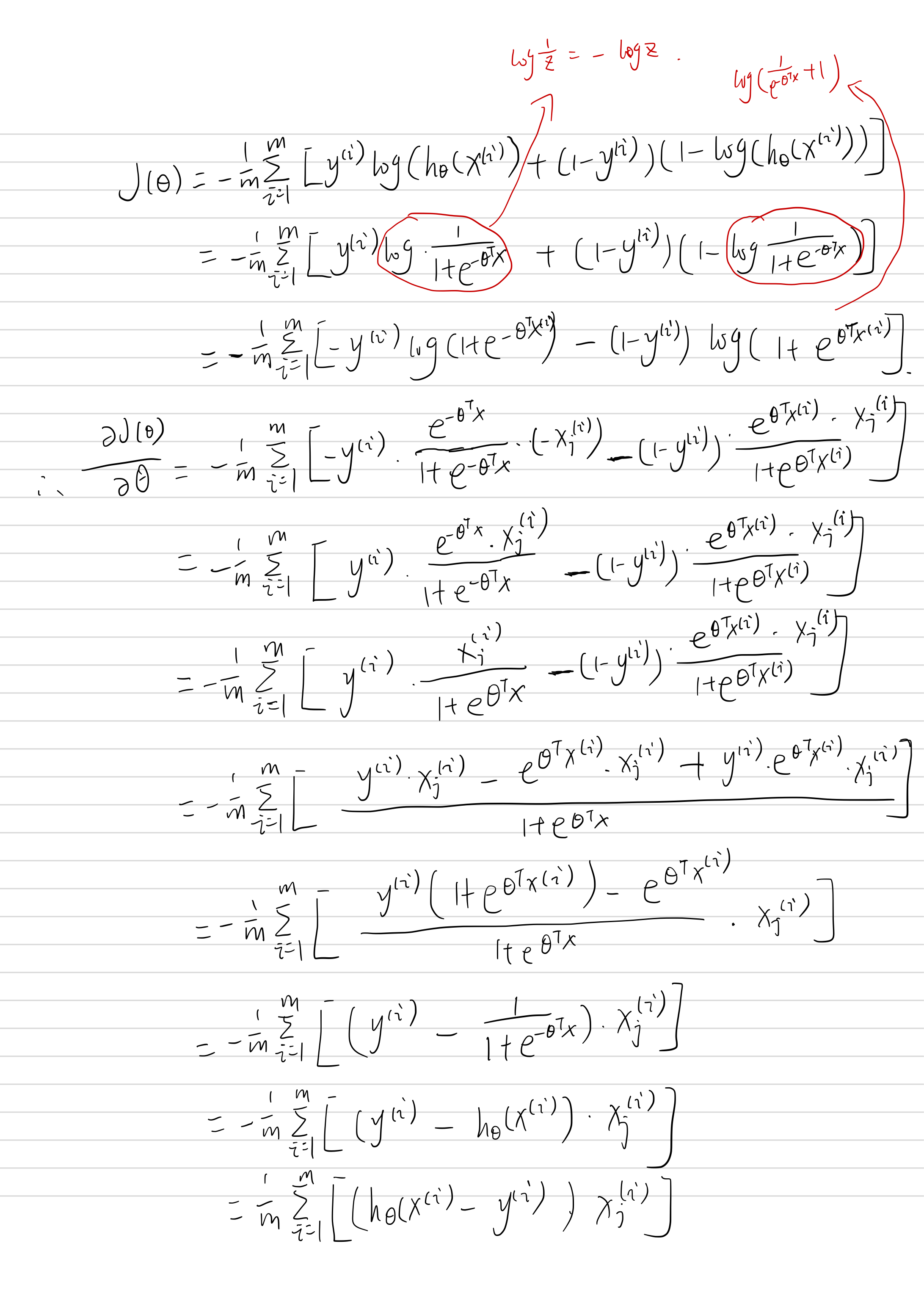
2、正则化

正则化的思想是，前面的参数会使得函数变得很大，如果想要最小化整个函数的话，那么正则化部分的必须要小才能满足要求（可以将压缩到接近0）。一般正则化不对增加惩罚项，只对1到n，只是约定俗成的，就算对0惩罚也没有什么影响。一般我们不知道是哪个参数导致过拟合，所以我们惩罚所有的参数。那么，加了惩罚项的损失函数为（一逻辑回归为例）：

上述模型加的是正则化，当然也可以用正则化。

经过正则化后，线性回归的代价函数变为：

线性回归的梯度下降算法变为：

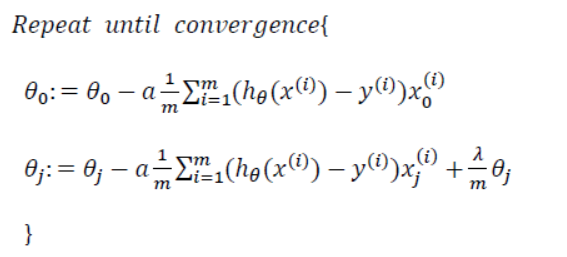
而逻辑回归的代价函数变为：

梯度下降算法变为：

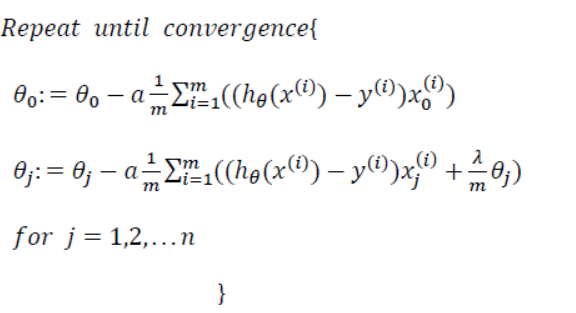
两种算法的是不一样的，虽然看上去形式一样。