本期专栏给大家介绍一篇我们组发表于ACM SIGMOD 2020的论文，是一篇关于大图上单源SimRank精确查询的算法论文，由中国人民大学和北京理工大学合作完成，第一作者为中国人民大学博士生王涵之，通讯作者为中国人民大学魏哲巍教授。论文具体信息如下：
论文链接，Technical Report，ExactSim代码
专栏作者 | 王涵之，中国人民大学信息学院
前言：SimRank作为图节点相似度衡量方向的代表性算法，在链接预测、网络分析等领域均有广泛应用。然而，SimRank定义式对应的Power Method算法受限于其高昂的计算复杂度而无法应用于大规模图集，近年来提出的SimRank近似算法也因为缺乏精确结果（ground truths）而无法评估其性能的优劣。针对这一问题，本篇论文提出了首个支持大规模图集上单源SimRank精确计算的算法ExactSim，该算法可以在一小时内返回拥有十亿条边的超大规模图集上的单源SimRank的ground truths，打破了SimRank提出以来无法获得大图上单源结果准确值的困境，为SimRank近似算法的性能评估提供了依据，避免了现有的小图上比精度、大图上比效率的不合理近似算法评估现象出现。
关键词：单源SimRank，精确计算，理论保证
一、SimRank介绍：
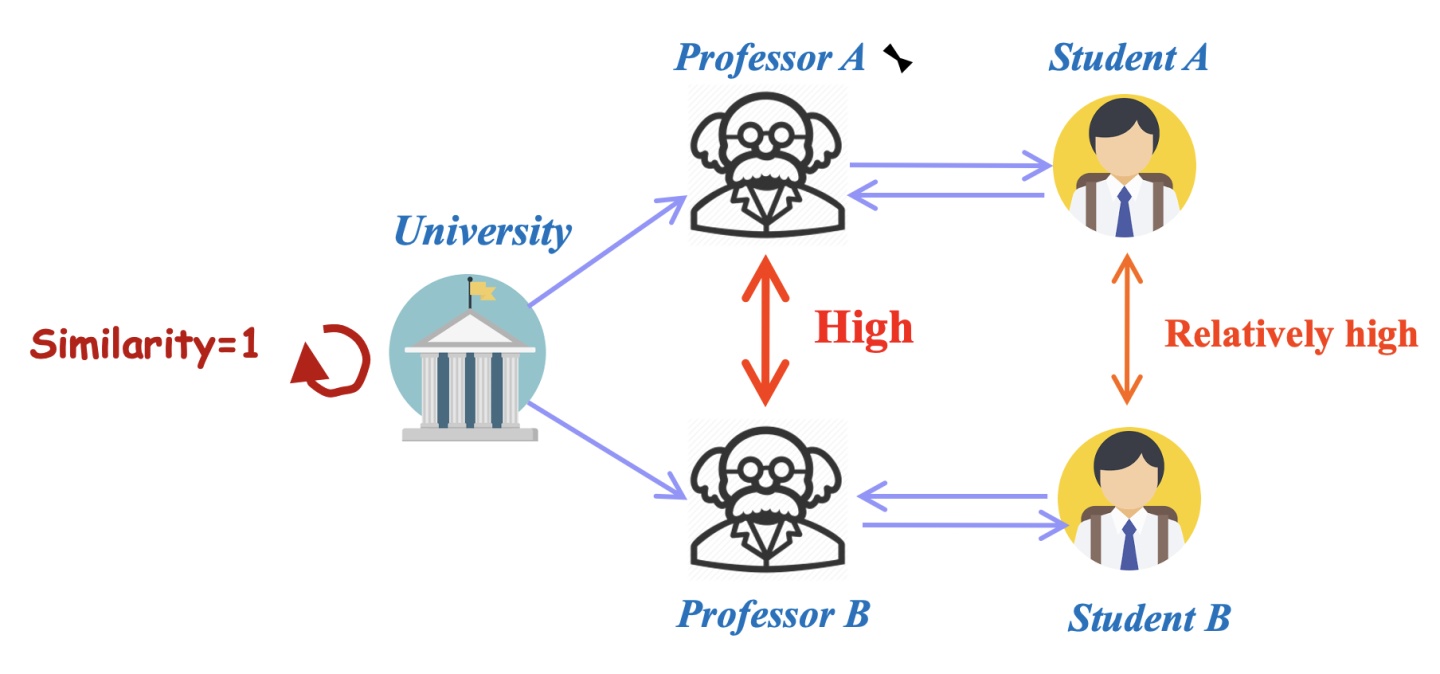
SimRank的概念最初由Glen Jeh和Jennifer Widom在2002年提出[1]，用于衡量图上两个节点之间的相似度。SimRank的直观思想可总结为以下两点：
- 一个节点和其本身的相似度最大。
- 如果两个节点各自的“邻居”节点是相似的，则这两个节点之间也具有相似性。
其具体定义如下：
其中，
在计算任意两个节点
本篇论文关心单源SimRank的查询问题，即给定图上某一节点
二、问题定义：
Power Method: SimRank的定义式给出了一种迭代计算的方法，我们称其为SimRank计算的Power Method，其在每一轮迭代中都依次更新图上所有节点对之间的SimRank值，由于衰减因子
单源SimRank近似算法：为了提高SimRank计算的可扩展性，近年来，很多研究者陆续提出了多种针对单源SimRank的近似算法，希望可以改进单源SimRank计算的时间和空间消耗，以期得到大图上的单源SimRank近似结果。根据算法的设计思路，我们可以将这些近似算法分为三类：基于线性加和式（Linearization）的方法，基于蒙特卡罗采样（Monte Carlo Sampling）的算法，和基于Local Push的算法。图 1 中对应列出了各类方法下部分有代表性的算法，有些算法同时使用了两类方法。
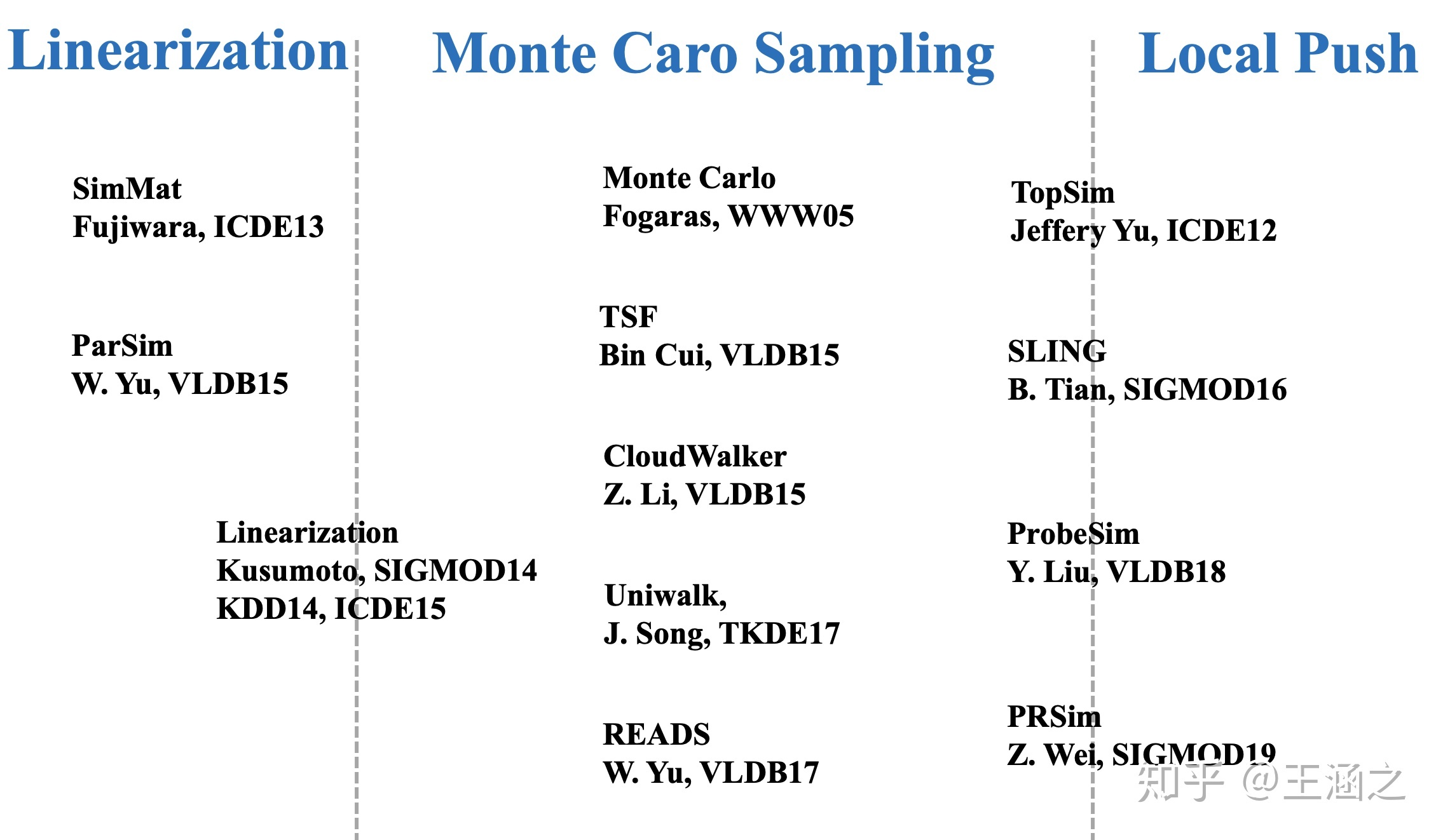
分析这些近似算法，我们发现，基于线性加和式（Linearization）的算法SimMat和ParSim修改了SimRank线性加和式中修正矩阵
值得注意的是，这里之所以希望得到
Motivation: 大图上缺乏单源SimRank的精确计算结果的现状会带来很多问题：
- 无法客观比较各近似算法的性能优劣，进而引发了在小图上比较算法准确性，在大图上比较算法运行速度的不合理现象出现。（例如，评估基于蒙特卡罗采样的两个近似算法，如果其中一个算法在小、大图上都从源节点出发产生固定条数的随机游走；另一个算法的随机游走条数根据图大小进行调整，小图上只产生较少的随机游走，大图上产生较多的随机游走。则即使第一个算法在小图上的结果准确率高于第二个算法、在大图上的计算速度远小于第二个算法，我们也无法得到算法 1 的性能表现较算法 2 更好的结论，这是因为如果算法 1 在大图上也只产生与小图上同样条数的随机游走，则在大图上的估计误差会远大于小图。
- 无法准确探知SimRank的分布和性质。
三、ExactSim算法：
针对上述问题，本篇论文提出了一种可以得到大图上单源SimRank精确解的算法ExactSim，其时间复杂度为
High-level ideas: ExactSim的设计思路中结合了算法 Linearization[2]和 PRSim[3]的思想，首先使用PRSim提出的针对修正矩阵
这里
PRSim[3]算法中提出了一种快速估计矩阵
Optimization: 在此基础上，本篇论文还提出了三种优化方法，用来进一步降低单源SimRank的计算时间和空间消耗。具体为：
- 矩阵
的局部确定性计算：为了提高矩阵
估计的准确程度，本篇论文提出，可以先确定性地算出前几层的不再相遇概率（即从节点
出发的两条
-游走在前
步不曾相遇的概率），再借助蒙特卡罗采样的方法估计得到其他层的不再相遇概率（即从节点
步不曾相遇的概率），进而降低蒙特卡罗采样的方差。
- 矩阵
采样估计时游走对的分配优化：在矩阵
条
出发的
- 线性化加和时向量的稀疏存储：优化算法指出，在线性化加和过程的每轮迭代中，不需要将
向量的每一维都进行存储，只需要存储其中大于绝对误差参数
的项即可。理论分析保证稀疏存储的操作在减少空间消耗的同时也不会放宽误差界。
四、实验评估：
本篇论文综合评估了所提算法ExactSim在小图和大图上的性能表现情况，并将ExactSim与各类单源SimRank计算方法中的state-of-the-art算法进行比较，即：基于线性加和式的最优算法Linearization[2]和ParSim[4]、基于蒙特卡罗采样的最优算法MC[5]、和基于Local Push的最优算法PRSim[3]。
数据集信息：
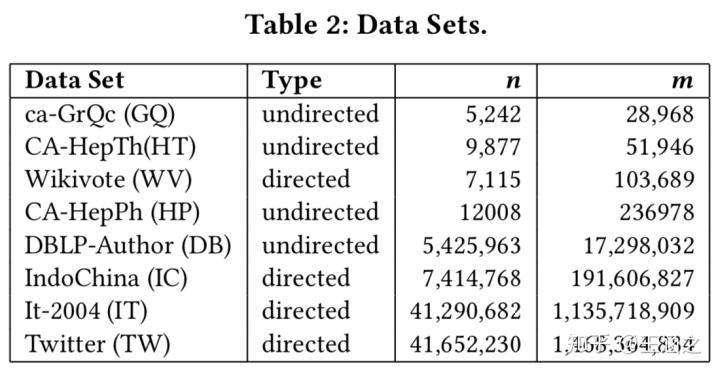
评价指标：
其中，
其中，
小图实验结果：
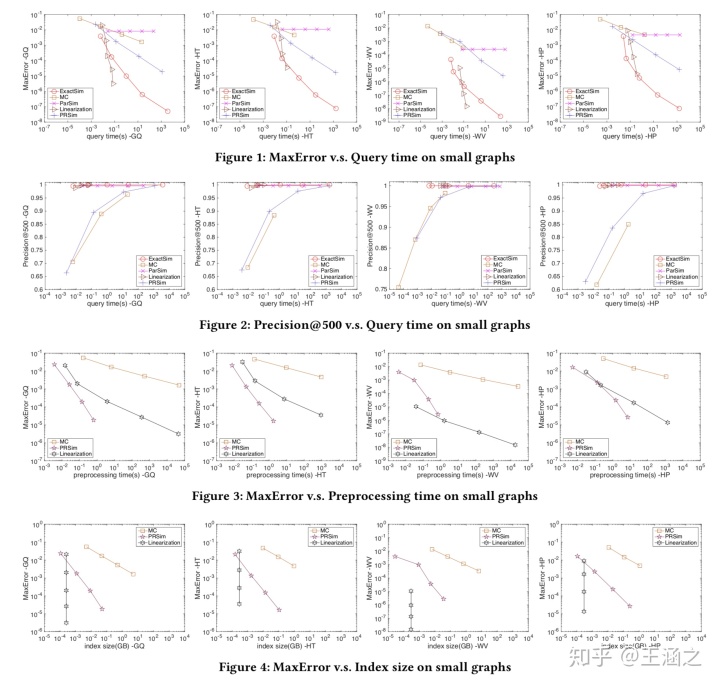
观察小图上的实验结果，可以看到，ExactSim是所有算法中唯一一个可以在四个数据集上连续取得
大图实验结果：
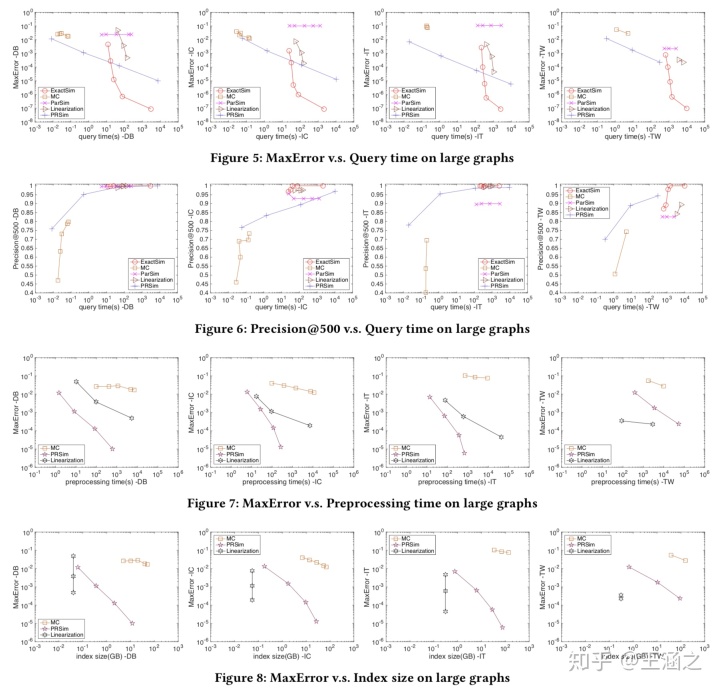
Power Method算法高昂的时间、空间复杂度使其无法求得大图上的ground truths结果，因此，本篇论文首先通过严格的理论分析保证了ExactSim的结果准确性，再使用ExactSim算法在
观察大图上的实验结果，可以看到，ExactSim算法的
五、论文回顾：
- 本篇论文提出了算法ExactSim，其是首个可以在有效时间内得到大图上
误差内的单源SimRank结果，如果用float类型变量存储SimRank结果，则ExactSim可以得到大图上单源SimRank的准确值。
- 本篇论文首先用理论分析保证了ExactSim算法的结果准确性，并通过大量的实验验证了ExactSim算法的有效性。
参考文献：
[1] Jeh G, Widom J. SimRank: a measure of structural-context similarity[C]//Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining. 2002: 538-543.
[2] Maehara T, Kusumoto M, Kawarabayashi K. Efficient simrank computation via linearization[J]. arXiv preprint arXiv:1411.7228, 2014.
[3] Wei Z, He X, Xiao X, et al. Prsim: Sublinear time simrank computation on large power-law graphs[C]//Proceedings of the 2019 International Conference on Management of Data. 2019: 1042-1059.
[4] Yu W, McCann J. Efficient partial-pairs SimRank search on large graphs[J]. Proceedings of the VLDB Endowment, 2015, 8(5): 569-580.
[5] Fogaras D, Rácz B. Scaling link-based similarity search[C]//Proceedings of the 14th international conference on World Wide Web. 2005: 641-650.
1329
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
