引言
有那么几天没更新博客了,发现到了不得不写的地步,总是有那么个声音在强迫自己,虽然工作很累,但是有些东西不写出来,不能原谅自己。今天为什么总结这两个关键字的区别,总觉得这两个关键字的用法用的太习惯了,没想过为什么这么用,就好比为什么一直用右手拿筷子,这么习惯。为什么我要用右手拿筷子,为什么不用左手呢?突然你就这么干了,发现你和周边很不协调,而且还夹不了菜。const和readonly也一样,习惯了,一直这样用,也就没追究过。突然被那么一问,还真说不出来个一二,今天就细细的研究下,到底这东东是啥玩意儿?网上虽然很多这方面的内容,虽然也看过,但是那毕竟是别人总结的,自己没动手实践一下,就觉得那不是自己的。实践才能记得更深刻,理解的更深。
常量
静态常量:指编译器在编译时会对常量进行解析,并将常量的值替换成初始化的那个值。
动态常量:在运行的那一刻获取值,编译器编译期间将其标识为只读常量,而不用常量的值代替,这样动态常量不必在声明的时候就初始化,而可以延迟到构造函数中初始化。
readonly和const
const修饰的常量为静态常量,而readonly修饰的常量为动态常量。
如何区别呢?
const修饰的常量在声明的时候必须初始化,readonly修饰的常量则可以延迟到构造函数中初始化。
const修饰的常量在编译期间就被解析,即常量值被替换成初始化的值,readonly修饰的常量则延迟到运行的时候。
const修饰的常量注重的是效率,readonly修饰的常量注重灵活。
const修饰的常量没有内存的消耗,readonly因为需要保存常量,所以有内存消耗。
const只能修饰基元类型。枚举类或者字符串类型,readonly却没有这个限制。
题一:
1 using System; 2 using System.Collections.Generic; 3 using System.Linq; 4 using System.Text; 5 using System.Threading.Tasks; 6 7 namespace Wolfy.ConstReadonly 8 { 9 class Program 10 { 11 static readonly int A = 2 * B; 12 static readonly int B = 4; 13 static void Main(string[] args) 14 { 15 Console.WriteLine("A={0},B={1}", A, B); 16 Console.Read(); 17 } 18 } 19 }
那么A=?,B=?,知道的先忍着,看一下到底是多少:
为什么会这样呢?ILspy看一下,到底是咋回事?
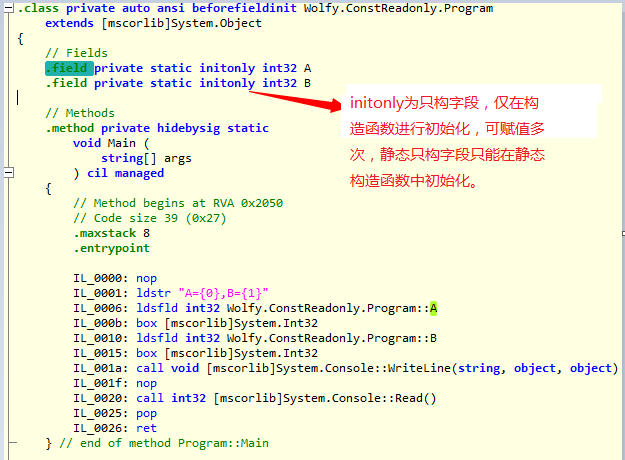
通过这也看不到什么不同啊,不要急,慢慢来,对比一下就知道不同了。
说明一下静态只构字段:
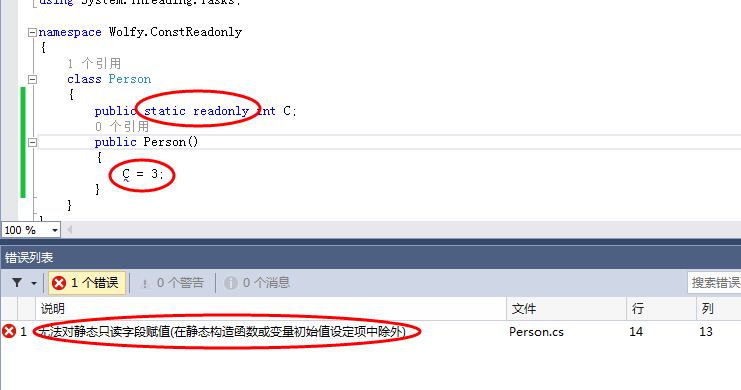
改为下面的就可以了:
1 using System; 2 using System.Collections.Generic; 3 using System.Linq; 4 using System.Text; 5 using System.Threading.Tasks; 6 7 namespace Wolfy.ConstReadonly 8 { 9 class Person 10 { 11 public static readonly int C; 12 static Person() 13 { 14 C = 3; 15 } 16 } 17 }
写这个主要是为了说明上面图中红色字描述的静态只构字段。
那么我们把readonly改为const试一试。
题二:
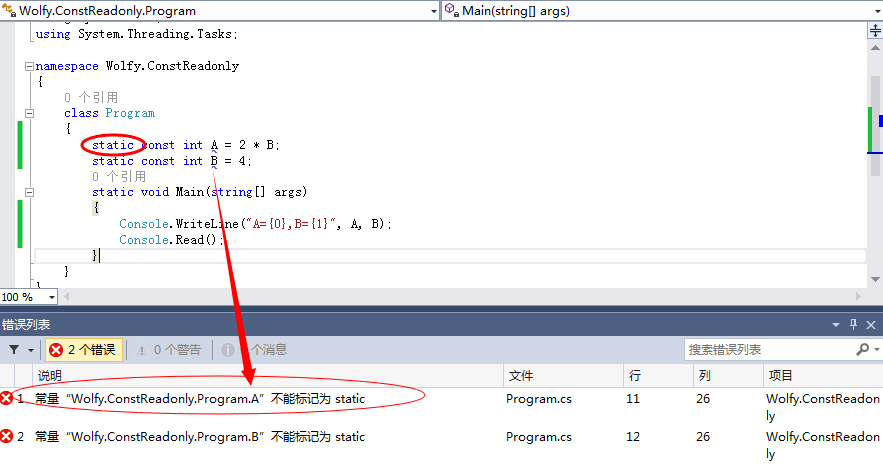
这个题,主要是考察static能不能和const关键字同时修饰一个变量,编译发现报错。
题三:
1 using System; 2 using System.Collections.Generic; 3 using System.Linq; 4 using System.Text; 5 using System.Threading.Tasks; 6 7 namespace Wolfy.ConstReadonly 8 { 9 class Program 10 { 11 const int A = 2 * B; 12 const int B = 4; 13 static void Main(string[] args) 14 { 15 Console.WriteLine("A={0},B={1}", A, B); 16 Console.Read(); 17 } 18 } 19 }
那么A=?,B=?,知道的,也别急,先忍着,看一下到底是多少:
那么这个面试题的IL是什么样子的呢?这里为了方便对比,将readonly的IL部分贴到一起,方便对比。
const修饰的常量在编译期间就被解析,即常量值被替换成初始化的值,readonly修饰的常量则延迟到运行的时候。
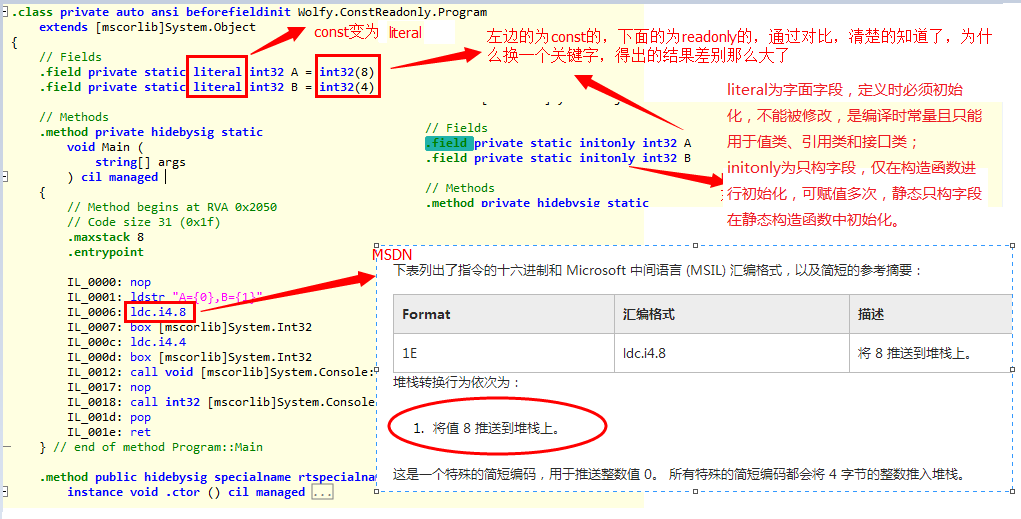
通过IL的对比,对他们的区别有了更深的认识了吧。希望对你有所帮助。
题四:
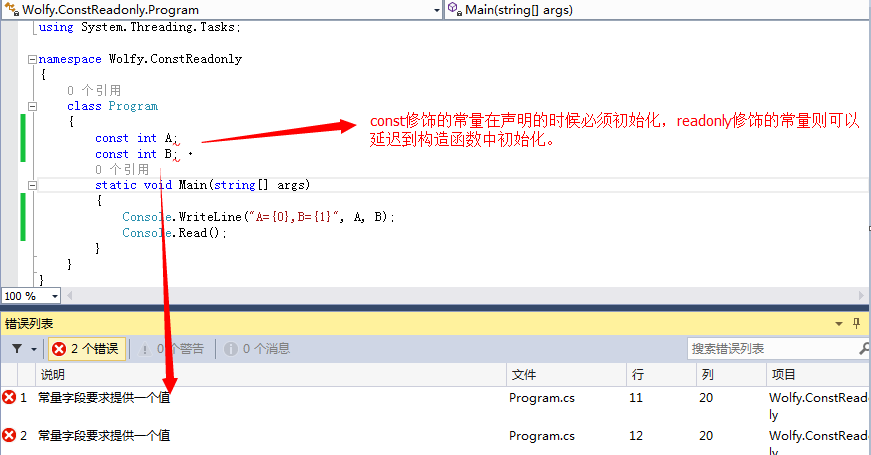
这个考察的主要是const修饰的常量必须初始化。
总结
东西很基础,只是想研究个究竟的时候,通过IL看了一下,虽然基础,如果通过IL一探究竟的话,还是收获颇深的,如果对你有所帮助不妨推荐一下。谢谢!
参考文章:http://blog.csdn.net/shellching/article/details/8516789




 本文深入探讨了C#中const与readonly关键字的区别,通过实际案例和中间语言(IL)对比,详细解释了静态与动态常量的概念及应用场景。
本文深入探讨了C#中const与readonly关键字的区别,通过实际案例和中间语言(IL)对比,详细解释了静态与动态常量的概念及应用场景。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








