[HDU5828]Rikka with Sequence

题意：维护一个数列，支持区间加，区间开根下取整，区间求和

最暴力的想法当然是用线段树维护，对于开根，如果当前区间内的数全相同，那么打一个覆盖标记，否则递归处理

这样当然是会被卡掉的：对于数列$\{2,3,2,3,\cdots\}$，重复$+6$和开根操作，这样就可以把上面那种暴力做法卡掉了

但其实这种暴力已经离正解很近了，考虑维护区间极差，如果递归到当前区间的极差$\geq2$，那么按暴力的方法做，否则分情况打一个区间减标记或者覆盖标记

为什么这样是对的？不妨设区间最小值为$mn$，最大值为$mx$，且$mx-mn\geq2$，那么$\left\lfloor\sqrt{mx+d}\right\rfloor-\left\lfloor\sqrt{mn+d}\right\rfloor=\left\lfloor\sqrt{mn+d+(mx-mn)}\right\rfloor-\left\lfloor\sqrt{mn+d}\right\rfloor$

考虑函数$f(x)=\left\lfloor\sqrt{x}\right\rfloor$

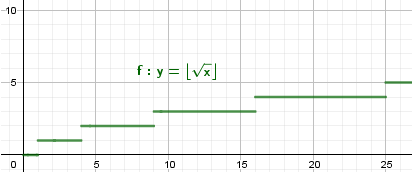
容易发现对任意的$d\geq2$，$f(x+d)-f(x)\lt d$

有了这个结论，上面的式子告诉我们一段极差$\geq2$的数开根下取整后极差会变小，而且开根本来就让数字减小得很快，所以对极差$\geq2$的区间，暴力也可以保证复杂度

那个用来卡暴力的数据告诉我们极差$=1$的情况要特别处理，如果$\sqrt{mx}=\sqrt{mn}$，打上覆盖标记，如果$\sqrt{mx}=\sqrt{mn}+1$，打上区间减标记

#include<stdio.h>
#include<math.h>
#define ll long long
#define inf 9223372036854775807ll
int p[100010];
ll s[400010],d1[400010],d2[400010],mx[400010],mn[400010];
//v'=d1*v+d2
void gao(int x,ll len,ll f1,ll f2){
	d1[x]*=f1;
	d2[x]=d2[x]*f1+f2;
	s[x]=s[x]*f1+len*f2;
	mx[x]=mx[x]*f1+f2;
	mn[x]=mn[x]*f1+f2;
}
void pushdown(int x,int l,int r){
	int mid=(l+r)>>1;
	if(d1[x]!=1||d2[x]){
		gao(x<<1,mid-l+1,d1[x],d2[x]);
		gao(x<<1|1,r-mid,d1[x],d2[x]);
		d1[x]=1;
		d2[x]=0;
	}
}
ll min(ll a,ll b){return a<b?a:b;}
ll max(ll a,ll b){return a>b?a:b;}
void pushup(int x){
	s[x]=s[x<<1]+s[x<<1|1];
	mx[x]=max(mx[x<<1],mx[x<<1|1]);
	mn[x]=min(mn[x<<1],mn[x<<1|1]);
}
void modify(int L,int R,ll f1,ll f2,int l,int r,int x){
	if(L<=l&&r<=R)return gao(x,r-l+1,f1,f2);
	pushdown(x,l,r);
	int mid=(l+r)>>1;
	if(L<=mid)modify(L,R,f1,f2,l,mid,x<<1);
	if(mid<R)modify(L,R,f1,f2,mid+1,r,x<<1|1);
	pushup(x);
}
ll querysum(int L,int R,int l,int r,int x){
	if(L<=l&&r<=R)return s[x];
	pushdown(x,l,r);
	int mid=(l+r)>>1;
	ll ans=0;
	if(L<=mid)ans+=querysum(L,R,l,mid,x<<1);
	if(mid<R)ans+=querysum(L,R,mid+1,r,x<<1|1);
	return ans;
}
void sqrt(int L,int R,int l,int r,int x){
	if(L<=l&&r<=R&&mx[x]-mn[x]<=1){
		ll sqx,sqn;
		sqx=sqrt(mx[x]);
		sqn=sqrt(mn[x]);
		if(sqx==sqn)
			gao(x,r-l+1,0,sqx);
		else
			gao(x,r-l+1,1,sqx-mx[x]);
		return;
	}
	pushdown(x,l,r);
	int mid=(l+r)>>1;
	if(L<=mid)sqrt(L,R,l,mid,x<<1);
	if(mid<R)sqrt(L,R,mid+1,r,x<<1|1);
	pushup(x);
}
void build(int l,int r,int x){
	d1[x]=1;
	d2[x]=0;
	if(l==r){
		s[x]=mx[x]=mn[x]=p[l];
		return;
	}
	int mid=(l+r)>>1;
	build(l,mid,x<<1);
	build(mid+1,r,x<<1|1);
	pushup(x);
}
int main(){
	int t,n,m,i,op,l,r,x;
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);
		for(i=1;i<=n;i++)scanf("%d",p+i);
		build(1,n,1);
		while(m--){
			scanf("%d%d%d",&op,&l,&r);
			if(op==1){
				scanf("%d",&x);
				modify(l,r,1,x,1,n,1);
			}
			if(op==2)sqrt(l,r,1,n,1);
			if(op==3)printf("%lld\n",querysum(l,r,1,n,1));
		}
	}
}

转载于:https://www.cnblogs.com/jefflyy/p/8555031.html