HDOJ(HDU) 1799 循环多少次？(另类杨辉三角)

Problem Description
我们知道，在编程中，我们时常需要考虑到时间复杂度，特别是对于循环的部分。例如，
如果代码中出现
for(i=1;i<=n;i++) OP ;
那么做了n次OP运算，如果代码中出现
fori=1;i<=n; i++)
for(j=i+1;j<=n; j++) OP;
那么做了n*(n-1)/2 次OP 操作。
现在给你已知有m层for循环操作，且每次for中变量的起始值是上一个变量的起始值＋1（第一个变量的起始值是1），终止值都是一个输入的n，问最后OP有总共多少计算量。

Input
有T组case，T<=10000。每个case有两个整数m和n，0< m< =2000，0< n<=2000.

Output
对于每个case，输出一个值，表示总的计算量，也许这个数字很大，那么你只需要输出除1007留下的余数即可。

Sample Input
2
1 3
2 3

Sample Output
3
3

这道题利用 排列组合Cn(m)（也就是从n个元素中任取m个元素）的思考方式，实现过程用杨辉三角（因为杨辉三角的值 可以对1007取余并保存）。
现在解释一下为什么这道题跟排列组合有关：
假设现在有4个 小球 A B C D 要从中取2个 用排列组合的方式：先取A 然后依次取 B C D ；接下来 取B 然后依次取C D ；接下来取C 只能 取剩下的D 这样就有3 + 2 + 1 = 6 种组合。
这里的4 就是题目的n 这里的2就是题目的m（循环次数）；
如果 循环次数为3 那么 先取A 再取B 然后依次 取 C D；
所以题目问的操作次数 也就是 问有多少种取球方式；

解题思路：求类似这样的问题。第一次怎么样。第二次怎么样，必定存在一定的规律，或是函数关系，或是递归。耐心写下几组。甚至几十组測试数据 ，你就会慢慢发现当中的联系。

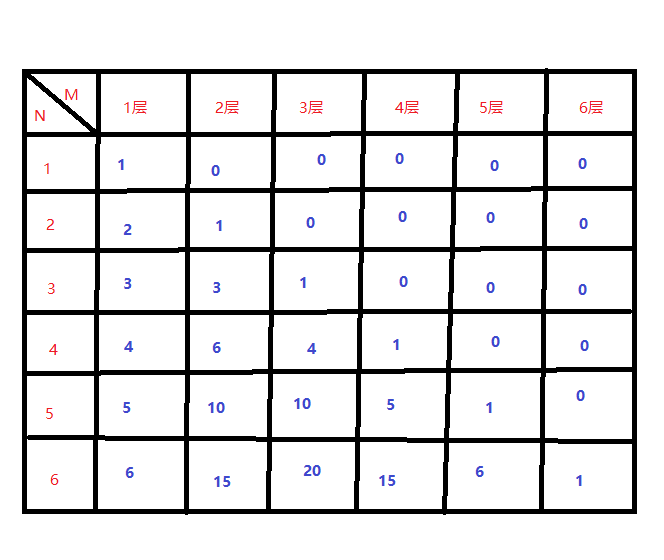
本题最重要的是建立模型 你会发现这是一个杨辉三角模型：

import java.util.Scanner;

public class Main{
    static int db[][] = new int[2005][2005];
    public static void main(String[] args) {
        dabiao();
        Scanner sc = new Scanner(System.in);

        int t =sc.nextInt();
        while(t-->0){
            int m =sc.nextInt();
            int n = sc.nextInt();
            System.out.println(db[n][m]);
        }

    }
    private static void dabiao() {
        for(int i=1;i<=2000;i++){
            db[1][i]=0;
            db[i][1]=i%1007;
        }
        for(int i=2;i<=2000;i++){
            for(int j=2;j<=i;j++){
                db[i][j] = (db[i-1][j]+db[i-1][j-1])%1007;
            }
        }
    }

}