C/C++ Quick Sort Algorithm

本系列文章由 @YhL_Leo 出品，转载请注明出处。
文章链接： http://blog.csdn.net/yhl_leo/article/details/50255069

---

快速排序算法，由C.A.R.Hoare于1962年提出，算法相当简单精炼，基本策略是随机分治。首先选取一个枢纽元（pivot），然后将数据划分成左右两部分，左边的大于（或等于）枢纽元，右边的小于(或等于枢纽元)，最后递归处理左右两部分。分治算法一般分成三个部分：分解、解决以及合并。快排是就地排序，所以就不需要合并了。只需要划分（partition）和解决（递归）两个步骤。因为划分的结果决定递归的位置，所以Partition是整个算法的核心。快速排序最佳运行时间O(nlogn)，最坏运行时间O(n2)，随机化以后期望运行时间O(nlogn)。

首先来看一段升序快速排序算法的实现代码：

#include <iostream>

using namespace std;

void quickSort(int arr[], int first, int last);
void printArray(int arr[], const int& N);

void main()
{
    int test[] = { 1, 12, 5, 26, 7, 14, 3, 7, 2 };
    int N = sizeof(test)/sizeof(int);

    cout << "Size of test array :"  << N << endl;

    cout << "Before sorting : " << endl;
    printArray(test, N);

    quickSort(test, 0, N-1);

    cout << endl << endl << "After sorting : " << endl;
    printArray(test, N);
}

/**
 * Quicksort.
 * @param a - The array to be sorted.
 * @param first - The start of the sequence to be sorted.
 * @param last - The end of the sequence to be sorted.
*/
void quickSort(int arr[], int left, int right) 
{
    int i = left, j = right;
    int tmp;
    int pivot = arr[(left + right) / 2];

    /* partition */
    while (i <= j) 
    {
        while (arr[i] < pivot)
            i++;
        while (arr[j] > pivot)
            j--;
        if (i <= j) 
        {
            tmp = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp;
            i++;
            j--;
        }
    }

    /* recursion */
    if (left < j)
        quickSort(arr, left, j);
    if (i < right)
        quickSort(arr, i, right);
}

/**
 * Print an array.
 * @param a - The array.
 * @param N - The size of the array.
*/
void printArray(int arr[], const int& N)
{
    for(int i = 0 ; i < N ; i++)
        cout << "array[" << i << "] = " << arr[i] << endl;
} 

1 划分（Partition）

划分分为两个步骤：

• 选取枢纽元
• 根据枢纽元所在位置将数组分为左右两部分

1.1 选取枢纽元

所谓的枢纽元，也就是将数组分为两部分的参考元素，选取的方式并不唯一。对于完全随机的数据，枢纽元的选取不是很重要，往往可以直接选取数组的初始位置的元素作为枢纽元。但是实际中，数据往往是部分有序的，如果仍然使用数组两端的数据作为枢纽元，划分的效果往往不好，导致运行时间退化为O(n2)。因此，这里给出的代码就是选取数组中间位置元素：

int pivot = arr[(left + right) / 2];

也有三数取中的方法、随机选取法等。

1.2 根据枢纽元分为左右两部分

上文算法代码使用的是Hoara的双向扫描方法：

/* partition */
while (i <= j) 
{
    while (arr[i] < pivot)
        i++;
    while (arr[j] > pivot)
        j--;
    if (i <= j) 
    {
        tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
        i++;
        j--;
    }
}

除此以外还有单向扫描，双向扫描（区别于Hoara的方法）以及改进的双向扫描等。

1.3 关于双向扫描的思考

• 内层循环中的while循环条件是用<=/>=还是</>。
  
  • 一般的想法是用<=/>=，忽略与枢纽元相同的元素，这样可以减少不必要的交换，因为这些元素无论放在哪一边都是一样的。但是如果遇到所有元素都一样的情况，这种方法每次都会产生最坏的划分，也就是一边1个元素，令一边n−1个元素，使得时间复杂度变成O(n2)。而如果用严格</>，虽然两边指针每此只挪动1位，但是它们会在正中间相遇，产生一个最好的划分。
  • 也有人分析，认为内循环使用严格</>，可以减少内循环。
  • 因此，建议内循环使用</>。
• 小数组的特殊处理
  
  • 按照上面的方法，递归会持续到分区只有一个元素。而事实上，当分割到一定大小后，继续分割的效率比插入排序要差。由统计方法得到的数值是50左右，也有采用20的，这样quickSort函数就可以优化成：

void newQuickSort(int arr[], int left, int right, int thresh)
{
    if(right - left > thresh)
    {
        // quick sort for large array
        quickSort(arr, left, right);
    }
    else
    {
        // insertion sort for small array
        insertionSort(arr, left, right);
    }
}

2 递归（Recursive）

即重复上述的划分（Partition）操作，最底层的情形是数列的大小是0或者1。快速排序算法和大多数分治排序方法一样，都有两次递归调用，但是快速排序的递归在函数尾部，因此可以实施尾递归优化，从而缩减堆栈的深度，减少算法的时间复杂度。

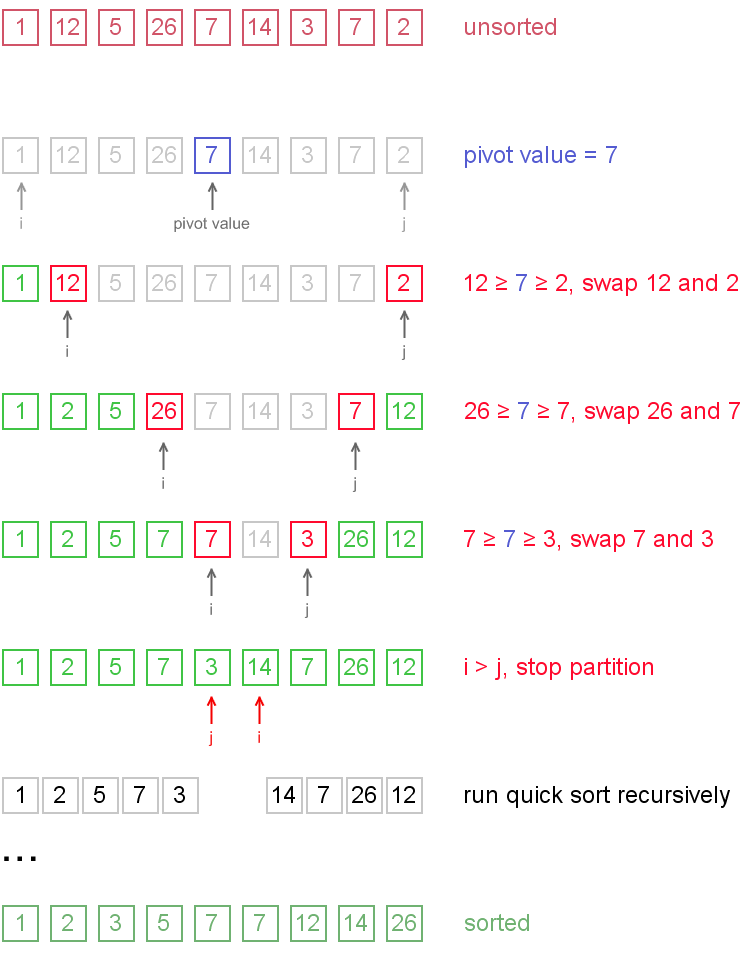
最后，贴上前文代码运行的过程：

---

参考文献

• http://www.algolist.net/Algorithms/Sorting/Quicksort

• http://mathbits.com/MathBits/CompSci/Arrays/Quick.htm

• http://codereview.stackexchange.com/questions/77782/quick-sort-implementation

• https://gsamaras.wordpress.com/code/quicksort-c/

• http://blogread.cn/it/article/612?f=sa

转载于:https://www.cnblogs.com/hehehaha/p/6332205.html