一、原理
它是建立在极大似然原理的基础上的一个统计方法,极大似然原理的直观想法是:一个随机试验如有若干个可能的结果A,B,C,…。若在仅仅作一次试验中,结果A出现,则一般认为试验条件对A出现有利,也即A出现的概率很大。一般地,事件A发生的概率与参数theta相关,A发生的概率记为P(A,theta),则theta的估计应该使上述概率达到最大,这样的theta顾名思义称为极大似然估计。
二、步骤
三、举例分析
极大似然估计,顾名思义是一种估计方法。既然是一种估计方法,我们至少必须搞清楚几个问题:估计什么?需要什么前提或假设?如何估计?估计的准确度如何?
直观概念,最大似然估计:
给定:模型(参数全部或者部分未知)和数据集(样本)
估计:模型的未知参数。
基本思想:
这一方法是基于这样的思想:我们所估计的模型参数,要使得产生这个给定样本的可能性最大。在最大释然估计中,我们试图在给定模型的情况下,找到最佳的参数,使得这组样本出现的可能性最大。举个极端的反面例子,如果我们得到一个中国人口的样本,男女比例为3:2,现在让你估计全国人口的真实比例,你肯定不会估计为男:女=1:0。因为如果是1:0,不可能得到3:2的样本。我们大多很容易也估计为3:2,为什么?样本估计总体?其背后的思想其实最是最大似然。
在机器学习的异常检测中,根据模型(通过学习得来的)计算一个数据点出现的概率,如果这个概率小于某个我们事先设定的值,就把它判为异常。我们基于的是一个小事件的思想:如果一件可能性极小的事情竟然发生了,那么就极有可能是异常。举个例子,我这辈子跟奥巴马成为哥们的可能性几乎为零,如果哪一天我跟奥巴马在烧烤摊喝3块钱一瓶的啤酒,那么绝对叫异常。
例子1:估计高斯分布的均值和方差
假设我们有一组来自高斯分布(均值和方差未知)的独立样本x[1]、x[2]、...、x[N],即
X[n] ~ N(u,t^2), n=1,2,...,N (注,本文中方差均匀t^2代替)
简单起见,我们假设这些观测值都是相同独立的,也就是这些观测值独立同分布(iid)。现在让你从这些样本中估计均值u和方差,如何下手?最大似然估计来帮你解决。
1)既然是idd,那么联合概率密度f(x[1],...,x[N]; u,t^2)=f(x[1] ; u,t^2)*...*f(x[N]; u,t^2),带入高斯分布得到:
我们把这个式子叫做似然函数,用来衡量从模型中产生这个样本组的可能性大小,我们记为L(x[1],...,x[n]; u,t^2).除以样本容量平均一下,就叫平均对数似然。这个函数有变量x[1],...x[N],还有u,t^2.现在我们换个角度看,把x[1]到x[N]看成是固定的,而u和t^2可能自由变化。根据基本思想,我们下一步就是要找到使得这个似然函数达到最大值的u和t^2的取值。
2)给定样本值之后,我们要求出上面式子最大值,由于ln函数是单调递增函数,我们将L取对数,得到
首先求L达到最大时u的值,取u的导数,令导数为0,得到u的估计值
接着把方差t^2看成一个变量,求导,令其等于零得到方差估计值
求解完毕。至于跟真实值差多少,计算比较复杂。有个定律是,如果有足够多的样本,那么我们可以使估计值达到任意的精度。极端情况下,样本就是总体,估计值就等于真实值。
例子2:人口比例
地球人都知道,概率模型中,取值可以使连续的(例子1就是),也可以是离散的。我们来看看离散的情况,人口比例。
假设现在有一个中国人口的样本组,样本容量为1000,服从独立同分布,男女比例为3:2.如何通过合理推到估计全国的人口比例(也就是证明样本估计总体的可行性)。一样用最大释然估计,我们现在的模型是个离散模型,我们假设其参数p为男性人口比例。现在要估计的就是这个p的值.
同上面一样,可以得到似然函数L=(p^600)*((1-p)^400),要求p,使得该函数最大,很简单,求导赋零,可以得到p=0.6.
值得说明的是,有些情况下可能存在多个模型参数,同时满足最大似然。另外有可能这个最佳的值是不存在的。最佳的模型参数拟合样本的函数是最好的。
最大似然估计也是统计学习中经验风险最小化(RRM)的例子。如果模型为条件概率分布,损失函数定义为对数损失函数,经验风险最小化就等价于最大似然估计。
小结一下,最大似然估计是在给定模型(含有未知参数)和样本集的情况下,用来估计模型参数的方法。其基本思想是找到最佳的模型参数,使得模型实现对样本的最大程度拟合,也就使样本集出现的可能性最大。







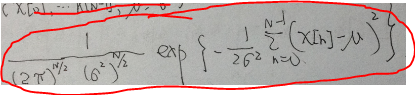
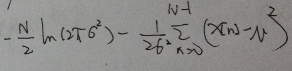
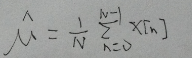
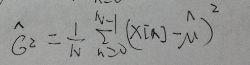














 9337
9337

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








