Solutions for the Maximum Subsequence Sum Problem

最新推荐文章于 2023-02-25 23:03:36 发布

AirZH??

最新推荐文章于 2023-02-25 23:03:36 发布

阅读量73

点赞数

原文链接：http://www.cnblogs.com/alantu2018/p/8471653.html

版权

The maximum subarray problem is the task of finding the contiguous subarray within a one-dimensional array of numbers (containing at least one positive number) which has the largest sum. For example, for the sequence of values −2, 1, −3, 4, −1, 2, 1, −5, 4; the contiguous subarray with the largest sum is 4, −1, 2, 1, with sum 6. --from wiki

下面我们分析四种算法的时间性能,由于运行时间相差较大，我们分成两组进行对比：

环境：ubuntu 12.04

时间单位：ms

时间性能：presume that the input is preread

第一组：输入数据元素个数2000

      C++ Code  
   

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

/*************************************************************************
    > File Name: algorithm1.c
    > Author: Simba
    > Mail: dameng34@163.com
    > Created Time: 2012年12月24日星期一 22时41分56秒
************************************************************************/

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<sys/time.h>

int maxsubsum1(const int a[], int n)
{
    int thissum, maxsum, i, j, k;

    maxsum = 0;
    for (i = 0; i < n; i++)
    {
        for (j = i; j < n; j++)
        {
            thissum = 0;
            for (k = i; k <= j; k++)
                thissum += a[k];

            if (thissum > maxsum)
                maxsum = thissum;
        }
    }
    return maxsum;
}

int maxsubsum2(const int a[], int n)
{
    int thissum, maxsum, i, j;

    maxsum = 0;
    for (i = 0; i < n; i++)
    {
        thissum = 0;
        for (j = i; j < n; j++)
        {
            thissum += a[j];

            if (thissum > maxsum)
                maxsum = thissum;
        }
    }
    return maxsum;
}

long GetTickCount(void)
{
    struct timeval tv;

    gettimeofday(&tv, NULL);

    return (tv.tv_sec * 1000 + tv.tv_usec / 1000);
}

int main(void)
{
    int i, n = 2000;
    int *ptr = malloc(sizeof(int) * n);
    srand(time(NULL));
    for (i = 0; i < n; i++)
        ptr[i] = rand() % 50 - 25;
    // adopt algorithm  1
    unsigned int utimecost = GetTickCount();
    int result = maxsubsum1(ptr, n);
    utimecost = GetTickCount() - utimecost;
    printf("max subsequence sum is %d, time cost %d\n", result, utimecost);

    // adopt algorithm  2
    utimecost = GetTickCount();
    result = maxsubsum2(ptr, n);
    utimecost = GetTickCount() - utimecost;
    printf("max subsequence sum is %d, time cost %d\n", result, utimecost);

    free(ptr);

    return 0;
}

输出为：

max subsequence sum is 275, time cost 4423
max subsequence sum is 275, time cost 6

第二组：输入数据元素个数 1000000

      C++ Code  
   

/*************************************************************************
    > File Name: divide_conquer.c
    > Author: Simba
    > Mail: dameng34@163.com
    > Created Time: 2012年12月24日星期一 23时24分41秒
************************************************************************/

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include <sys/time.h> /* struct timeval, gettimeofday(), struct itimerval, setitimer(), ITIMER_REAL */

int divide_conquer(int arr[], int start, int end)
{
    if(start == end)
        return (arr[start] > 0 ? arr[start] : 0);

    int mid = (start + end) / 2;
    int max_left = divide_conquer(arr, start, mid);
    int max_right = divide_conquer(arr, mid + 1, end);
    // mid subsequence

    int max_left_border = 0;
    int tmp_sum = 0;
    int i;

    for(i = mid; i >= start; i--)
    {
        tmp_sum += arr[i];
        if(tmp_sum > max_left_border)
            max_left_border = tmp_sum;
    }

    int max_right_border = 0;
    tmp_sum = 0;
    for(i = mid + 1; i <= end; i++)
    {
        tmp_sum += arr[i];
        if(tmp_sum > max_right_border)
            max_right_border = tmp_sum;
    }

    int max_mid = max_left_border + max_right_border;
    // max subsequence
    int iresult = max_left;
    if(max_right > iresult)
        iresult = max_right;
    if(max_mid > iresult)
        iresult = max_mid;
    return iresult;
}

int maxsubsum3(const int a[], int n)
{
    int j, thissum, maxsum;
    thissum = maxsum = 0;
    for (j = 0; j < n; j++)
    {
        thissum += a[j];

        if (thissum > maxsum)
            maxsum = thissum;
        else if (thissum < 0)
            thissum = 0;
    }

    return maxsum;
}

long GetTickCount(void)
{
    struct timeval tv;

    gettimeofday(&tv, NULL);

    return (tv.tv_sec * 1000 + tv.tv_usec / 1000);
}

int main(void)
{
    int i, n = 1000000;
    int *ptr = malloc(sizeof(int) * n);
    srand(time(NULL));
    for (i = 0; i < n; i++)
        ptr[i] = rand() % 50 - 25;
    // adopt divide_conquer algorithm
    unsigned int utimecost = GetTickCount();
    int result = divide_conquer(ptr, 0, n - 1);
    utimecost = GetTickCount() - utimecost;
    printf("max subsequence sum is %d, time cost %d\n", result, utimecost);
    // adopt algorithm 3
    utimecost = GetTickCount();
    result = maxsubsum3(ptr, n);
    utimecost = GetTickCount() - utimecost;
    printf("max subsequence sum is %d, time cost %d\n", result, utimecost);

    free(ptr);

    return 0;
}

输出为：

max subsequence sum is 2410, time cost 217
max subsequence sum is 2410, time cost 4

分析：

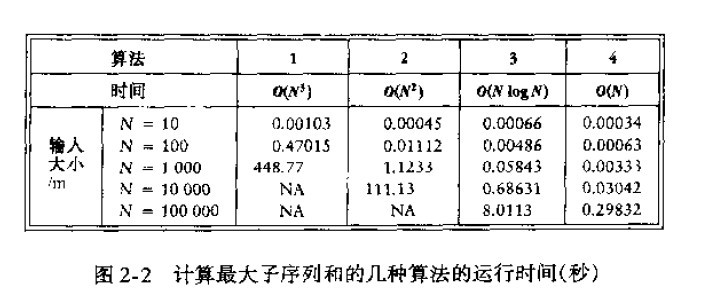
在《data structure and algorithm analysis in c》中有对这四种算法时间性能的分析，依次下来分别是O(n^3)，O(n^2)，O(nlogn)，O(n)，即使我们在第二组输入的元素个数是第一组的500倍，第二组的运行时间都要比第一组的小。下图2-2是作者写书时测试的时间列表，显然现在的机器运行得更快。