由蒙特卡罗方法所想到的

最新推荐文章于 2023-08-31 14:50:57 发布

weixin_34366546

最新推荐文章于 2023-08-31 14:50:57 发布

阅读量169

点赞数

文章标签：数据库 python java

原文链接：https://my.oschina.net/cain1507/blog/735633

版权

2019独角兽企业重金招聘Python工程师标准>>>

由蒙特卡罗方法所想到的

在测试一个项目推送流程的时候，猛地忽然想起了之前看过的一篇蒙特卡洛方法的入门。

蒙特卡罗方法是一种计算方法，原理是通过大量随机样本，去了解一个系统，进而得到所要计算的值。它诞生于上个世纪40年代美国的"曼哈顿计划"，名字来源于赌城蒙特卡罗，象征概率。早在17世纪，人们就知道用事件发生的"频率"来决定事件的"概率"。同样，在无法计算得到准确的概率的时候，我们可以精确的模拟场景的发生，统计其频率，从而获得某事发生的概率。

而我在对项目进行压力测试的过程当中，一直无法实现自己曾经设想的测试条件，只能退而求其次的想办法来使得测试尽可能准确。推送的流程很简单，我只需要往项目的推送接口推送数据即可，这里我还曾经在辛苦地看着Webservce的ws接口调用相关的东西~~~ 数据推送插入到数据库中不同的表中，但是手中可供测试的数据有限，只能用已有的有限数据来反复推送从而达到压力测试大量推送数据的效果，所以反复推送的数据必须反复地进行撤销，流程如下：

这个倒也不麻烦，写一个生产者消费者式的模型即可，只是需要调一些测试的参数。但是关键是我如何能保证我插入的测试数据是正确的呢？？？

我之前的设想是：推送过去，立马查询数据库，与发送数据进行比对即可知道插入数据库中是否正确，之后进行撤销即可。但是，项目并没有提供查询数据的接口，直接把项目中数据库的完整操作流程搬过来显得太重了，只是一个测试而已，没有必要把测试项目也弄得很大。所以有尝试过自己写一套轻量的数据库连接查询操作，但是毕竟对Mybatis、structs、Spring不熟悉，时间也有限，做了有限的尝试之后就放弃了，其实很不想说到放弃这个词，只是迫于时间的压力不得不选择新方法。

既然没办法实现对每笔数据进行查询校验，确保每条插入的数据都正确的话，那就尽量保证插入的数据是正确的就行了，就像生物中统计一个区域中某种生物的数量使用“标记重捕法”一样，先抓取100只全部标记，过一段时间再抓取一百只，看其中带有标记的动物的数量，从而估算中该生物总的数量。在测试中也一样，100笔数据分成两份，50笔重复发送重复撤销，另外50笔每发送50笔就插入一笔在其中，这样就相当于发送了2500笔数据，如果这50笔数据都正确的无误的话，那就基本能代表插入2500笔数据也正确无误。

有点不太严谨，但是毕竟不是性能测试，压力测试只是为了验证新的流程是否会出问题而已。所以有些实际的问题用概率论上的方法解决还是挺有趣的，比如当初用蒙卡罗特方法计算圆周率 π , 正方形内部有一个相切的圆，它们的面积之比是π/4。

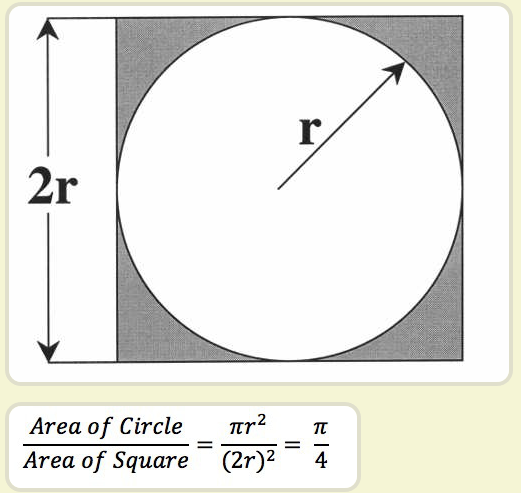
现在，在这个正方形内部，随机产生10000个点（即10000个坐标对 (x, y)），计算它们与中心点的距离，从而判断是否落在圆的内部，如果这些点均匀分布，那么圆内的点应该占到所有点的 π/4，因此将这个比值乘以4，就是π的值。通过R语言脚本随机模拟30000个点，π的估算值与真实值相差0.07%。

程序也比较简单，自己也写了一下，代码如下：

import java.math.BigDecimal;
import java.math.MathContext;
import java.math.RoundingMode;
import java.util.Random;

public class TestPai {

   public static boolean isInsideCircle(int xPoint, int yPoint){
       return xPoint*xPoint + yPoint*yPoint <= 10000;
   }

   public static void main(String[] args) {

       Random random = new Random();
       int count = 0;
       int x = 0, y = 0;
       for(int i = 0; i < 80000; i++){
           x = random.nextInt(200) - 100;
           y = random.nextInt(200) - 100;
           if( isInsideCircle(x,y) ){
               count++;
           }
       }

       BigDecimal a=new BigDecimal(count);
       BigDecimal b=new BigDecimal(80000);
       MathContext mc = new MathContext(10, RoundingMode.HALF_DOWN);
       BigDecimal c = a.divide(b,mc);
       BigDecimal d = new BigDecimal(4);
       System.out.println( c.multiply(d, mc));

   }