在前一篇极其概略地描述了一个简单声明 "int x" 的生成 ast 的过程, 此篇打算
同样概略地描述一个简单表达式 "x+2" 的生成 ast 的大致过程. 因为在表达式
中会使用声明的变量, 以及一些基本的 tree_node 树节点结构, 所以先以一个
简单声明开始的.
实际上表达式 "x+2" 不能在 C 语言顶层(toplev) 上书写, 以及 x 需要实现声明,
所以实际最简单的出现该表达式的 C 程序看起来如下:
int x; // 或用 extern int.
int f() { // 或者用 int f(int x), 此时 x 是函数的参数.
x + 2; // 我们关心的表达式实际写在这里.
}
每次都写 int x; int f() 比较繁冗, 所以就省略掉这些外围的部分代码.
对于表达式的产生式部分, 使用前一篇中的方法论:
1. 自顶向下列出 parse 此例子相关的产生式, 并编号, 以方便指代.
2. 自底向上归约, 计算每个非终结符的语法值.
1. 一个 C 语句: (选择表达式的那个)
stmt -> expr:$1 ';' {$3}
2. 产生式 1.$1 :
expr -> nonnull_exprlist:$1 {$2}
3. 产生式 2.$1 :
nonnull_exprlist -> expr_no_commas:$1 {$2}
4. 产生式 3.$1 : (需要选择2个产生式)
4.1 expr_no_commas -> primary:$1;
4.2 expr_no_commas -> expr_no_commas:$1 '+' expr_no_commas:$3 {$4};
5. 产生式 4.1.$1:
5.1 primary -> IDENTIFIER:$1 {$2};
5.2 primary -> CONSTANT:$1;
====
下面按照自底向上地方式归约表达式 "x + 2 ;".
这个表达式由四个词法符号构成 标识符 "x", 加法符号 '+', 整数常量 2, 分号 ';'.
-- 归约 5.1
标识符 "x" 被按照产生式 5.1 归约.
5.1 primary -> IDENTIFIER:$1 {$2};
按照习惯, 终结符被写作大写的, 如 IDENTIFIER 表示词法器识别的标识符.
词法器为标识符返回的词法值为 IDENTIFIER, 词法器为该标识符建立一个 tree_identifier 节点,
其节点值可写作 (identifier_node x), 然后在当前词法域中查找该符号的声明(decl), 我们已假设
该符号("x") 被声明为一个全局变量 ("int x"), 则查找到的声明为 (var_decl int x), 这个声明被放入
到一个全局变量 lastiddecl 中.
关联代码块 $2:
$$ = lastiddecl; // 即 (var_decl int (identifier_node x))
(实际的代码块还有检查各种情况的代码, 我们暂时忽略, 只列出符合此实际例子的代码)
这样非终结符 primary 的语法值就是 (var_decl int x).
-- 归约 4.1
4.1 expr_no_commas -> primary:$1;
按照缺省语义动作 $$=$1, 此时非终结符 expr_no_commas 的语法值为 $1 即 (var_decl int x).
(这里可以在纸上进行推导, 然后调试程序以进行验证.)
顺便说一下, expr_no_commas 表示 C 表达式, 不含逗号分隔. 如 "x*2", 用逗号分隔的例子
是 "x, y-3, 4+z*5" 是一个 expr, 但是含三个 expr_no_commas.
-- 归约 5.2
此步骤归约(reduce) 整数常量 2. 该常量之前的 加法符号 '+' 被移入(shift) 到语法分析栈中,
此时该语法分析栈的内容是: [...前面的略... expr_no_commas '+' ), 其中 expr_no_commas
是上一个步骤归约的, '+' 是移入的.
5.2 primary -> CONSTANT:$1;
终结符 CONSTANT 是词法器识别并返回的, 其语法值是一个 tree_int_cst 类型的 tree_node,
我们写作 (int_const 2), 按照缺省语义动作, 非终结符 primary 的语法值为 (int_const 2).
此时再执行一次 4.1 的归约, 对应 expr_no_commas 的语法值为 (int_const 2).
这时语法分析栈的内容: [... expr_no_commas '+' expr_no_commas ), 已经具备了按照
产生式 4.2 归约为更大的一个 expr_no_commas 的条件.
-- 归约 4.2
4.2 expr_no_commas -> expr_no_commas:$1 '+':$2 expr_no_commas:$3 {$4};
由 $1 指代的那个 expr_no_commas 语法值为 (var_decl int x), 由 $3 指代的那个
expr_no_commas 的语法值为 (int_const 2), 它们都是 tree_node 的实例.
另外, 加号 '+' 在词法器中返回的语法值 $2 为 enum tree_code 类型的枚举值 PLUS_EXPR,
从名字看就知道是 '加法表达式'.
代码块 $4:
$$ = build_binary_op($2, $1, $3);
代入 $2, $1, $3 的值, 写为:
$$ = build_binary_op(PLUS_EXPR, (var_decl int x), (int_const 2))
函数 build_binary_op() 比较复杂, 我们先略过其过程(以后讨论), 看其返回的结果:
$$ = (plus_expr (var_decl int x) (int_const 2))
这里 plus_expr 表示构造了一个 tree_node 节点, 代码(code)是 PLUS_EXPR, 它的结构
对应为 struct tree_exp, 加法操作拥有两个操作数(operand), 此例分别是 x, 2.
我们从内向外的简化这个 $$ 值的写法, (var_decl int x) 简写为 x, (int_const 2) 简写为 2.
$$ = (plus_expr x 2), 再把 plus_expr 简写为 +, 则
$$ = (+ x 2), 则这样的结果看上去就是 lisp 表达式的样子了.
同样, 表达式 "x+y*2" 按照上面类似的方式归约, 简化, 最后的 expr_no_commas
的语法值就是 $$ = (+ x (* y 2)), 也是一个 lisp 表达式的样子.
-- 归约 3:
nonnull_exprlist -> expr_no_commas:$1 {$2}
nonnull_exprlist -> nonnull_exprlist ',' expr_no_commas (另一个产生式)
已知 $1 是一个表达式节点: (+ x 2), 代码块 $2 为:
$$ = build_tree_list(null, $1)
函数 build_tree_list() 相当于 Lisp 中的函数 cons(), 用于构造一个 list. 我们可以简写为:
$$ = ($1) = ((+ x 2)). // 外层括号表示列表, 里层括号表示 '+'表达式.
因为非终结符 nonnull_exprlist 表示 expr_no_commas 的列表, 多个 expr_no_commas
是通过 tree_list 连接起来的, 以 "x+2, y-3, 4+z*5" 例子来说, 对应的三个 expr_no_commas
为: (+ x 2), (- y 3) (+ 4 (* z 5)), 归约到 nonnull_exprlist 就成了 list:
( (+ x 2) (- y 3) (+ 4 (* z 5)) ) ...
所以我们说, Lisp 中的 list 在程序中经常出现...
所以最后非终结符 nonnull_exprlist 的语法值为 tree_list:(expr_no_commas+).
-- 归约 2:
expr -> nonnull_exprlist:$1 {$2}
已知 nonnull_exprlist 是 tree_list:(expr_no_commas+), 代码块 $2:
$$ = build_compound_expr($1)
这里函数 build_compound_expr() 我们先简化为仅使用 $1 表达式列表的最后一个
作为结果表达式返回. (多个逗号分隔的表达式, 按照 C 语言要求, 取值取最后一个表达式的).
这样非终结符 expr 是一个结构为 tree_exp 的 tree_node, 例子 "x+2" 中就是 (+ x 2) 这个
表达式节点. 更复杂的 compound_expr 以后我们有机会再探讨.
-- 归约 1:
stmt -> expr:$1 ';' {$3}
已知 $1 是一个表达式节点 tree_exp:(+ x 2), 代码块 $3 为:
expand_expr_stmt($1) // 仅留下核心部分, 其它无关的略.
函数 expand_expr_stmt() 的最核心的任务是将 tree_exp, 也就是 AST 转换为 RTL.
这个关键转换步骤是我们下一阶段要研究的重点, 但 parse 语法以构造 ast 过程到这里
是一个阶段的结束了. (意思是我们分清楚各个阶段, 就是在这个点划分和方便理解)
对于更加复杂的表达式, 我们在以后遇到的时候再研究.
==== 以下快速概览这种简单表达式从 ast 转换到 rtl 的过程.
在产生式 stmt -> expr ';' 的关联语义代码块中, 右侧的非终结符 expr 是表达式的 ast,
调用的函数 expand_expr_stmt(expr) 中完成从 ast 都 rtl 的转换. (可能该函数还进行别的
任务, 但就 ast->rtl 的转换任务, 该函数是主要完成的部分). 简而言之, 这个转换函数的
输入是 ast, 输出/产出是 rtl. (其内部使用关键性的庞大的 expand_expr() 函数完成任务)
为了研究 ast->rtl 的转换, 需要一些相关的理论和知识:
1. 知道 ast 的基本结构和一些基本 tree 节点知识 (前面提及过一小部分)
2. 知道 rtl 的基本结构, 少量 rtl 节点知识.
3. 从 ast->rtl 转换的基本思想.
其中 1,2 在 tree.def, rtl.def 文件中有基本的信息, 在所列参考网页上也有很多, 出于各种
原因(很可能是懒惰), 不想这里叙述更多了. 下面简要叙说 ast->rtl 基本思想.
已知 ast 是一颗树, rtl 也是树, 这转换是树之间转换, 基于 rtl 可用的指令操作数存储类型.
对于 ast 中任一个操作(如 +, *) 的对应的指令(如 add, mul), 这些指令的操作数的
存储类型(MEM, IMM, REG) 满足指令的要求, 则能直接转换. 如果不满足, 则需将子树
先归约为一个伪寄存器(pesudo REG) 以满足操作数存储分类的要求, 然后再转换.
转换的过程是在对 ast 树的后序遍历中实现(递归调用 expand_expr() 函数),
即自底向上的一次重写. (对于 1 个或多个操作数等情况也类似)
以一个表达式例子说明: "x + y*3". 这个表达式写作我们前面所述简化的 ast 为:
(+ x (* y 3)), 用图示更清晰如下(画得不好, 示意即可):
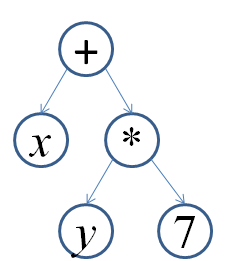
现在这颗树最终要变换为两个 rtl 树 (具体变换多少, 如何变换都与目标机器的指令集密切相关,
我这里描述的是缺省 i386 体系, 一般的情况下). x 子节点对应 MEM (内存地址操作数) 模式,
加法 + 接受这种 MEM 类型的作为其操作数. 但子树 (* y 7) 不能直接做操作数, 需要先归约.
该子树然后归约为(reduce)一个伪寄存器 r_10, 然后树 (+ x r_10) 变换为另一个 rtl. 归约产生
对展开函数 expand_expr() 的递归调用.
下面先给出最后发行的 rtl, 共两个:
1. (set (reg:SI 10)
(mult:SI (mem:SI (symbol_ref:SI ("y")))
(const_int 7)))
2. (set (reg:SI 11)
(plus:SI (reg:SI 10)
(mem:SI (symbol_ref:SI ("x")))))
看起来括号很多, 挺繁琐的不易弄懂, 为此我们使用两个方法来处理这个问题:
1. 使用 lisp 打印/排版惯例(方式), 将一个操作的多个操作数对齐排列.
上面是我已经排版好了的. (如果有工具, 这一步是可以自动做的...)
2. 从里到外简写, 以帮助理解. 和对 ast 的简写类似.
(这一步, 如果我们肯花时间写工具, 也是可以自动做的...)
(但是自己完成简写过程, 主要是为了理解, 所以自己做还是有意义的)
下面我们开始简写上面的 rtl 1:
(symbol_ref:SI ("y" 或 "x")) 表示对一个符号 y 或 x 的引用, 我们直接简写为 y 或 x.
(mem:SI y) 其中的 y 已经是被简写的符号了, mem 表示取 y 这个符号所在地址
中的数据, SI 表示机器模式 Single Integer (SI), 即从 y 这个地址取一个 SI 格式
的数字. 由于这里都是 SI 模式, 简写时候完全可以略去. 设简写为 ^y, 符号可以自己选,
只要方便理解即可(我选择这个像 pascal 指针写法, 方便理解即可).
(const_int 7) 简写为 7.
(mult:SI ^y 7) 简写为 (* ^y 7)
(reg:SI 10) 简写为 r_10. (编号为第 10 的伪寄存器)
(set r_10 (* ^y 7)) 简写为 (= r_10 (* ^y 7)), 这个样子写为中序表达式就是:
r_10 = ^y * 7
写成汇编形态就是:
mul ^y, 7 => r_10 也即: 取符号 y 处的内存(MEM) SI 类型操作数, 乘上 立即操作数(IMM) 7,
结果送入伪寄存器 r_10.
上面的 rtl 2 类似的简写为:
(= r_11 (+ r_10 ^x))
写成对应的汇编形态就是:
add r_10, ^x => r_11
这个形态距离最终的实际汇编代码就更近了一步了.
实际我测试时最终该 rtl 生成的汇编代码为:
imull $7, y, %eax ; imull: i有符号 long 乘法. $7 立即数 7, 符号y. 结果在 %eax
addl x, %eax ; x + %eax ==> %eax, l 后缀表示 long, 即 SI, Single Integer
从 rtl 再经历多个遍(pass) 优化等各种处理(据我看某文档, 说在 rtl 上有大约 70+ 种的各种 pass)
然而生成 asm 的过程, 属于第3阶段的转换问题. 我们本阶段研究 ast->rtl 就忽略它了.






















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








