(1-cosx)/(x^2)从负无穷到正无穷的积分怎么求?
这道题需要先进行简单地变形,然后利用帕塞瓦尔定理,再计算结果。
1.简单变形:
原式=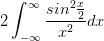
令 ,有
,有
……= ;
;
2.帕塞瓦尔等式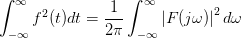
又
故原式= .
.
3.计算结果 在
在 时有非零值1,则易知原式=
时有非零值1,则易知原式= 。
。
(1-cosx)/(x^2)从负无穷到正无穷的积分怎么求?
这道题需要先进行简单地变形,然后利用帕塞瓦尔定理,再计算结果。
1.简单变形:
原式=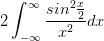
令 ,有
,有
……= ;
;
2.帕塞瓦尔等式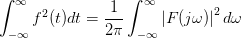
又
故原式= .
.
3.计算结果 在
在 时有非零值1,则易知原式=
时有非零值1,则易知原式= 。
。
转载于:https://my.oschina.net/u/658658/blog/466359
 2441
2441
 5156
5156
 332
332

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


