题目
求解 ∫ − ∞ + ∞ x sin x x 2 + 16 d x \int_{-\infty}^{+\infty}\frac{x\sin x}{x^2+16}\mathrm{d}x ∫−∞+∞x2+16xsinxdx
歪解
因为 y = x y=x y=x 是奇函数, y = sin x y=\sin x y=sinx 是奇函数, y = 1 x 2 + 16 y=\frac{1}{x^2+16} y=x2+161 是偶函数,奇函数乘上奇函数乘上偶函数为奇函数,奇函数在关于 0 对称的范围内积分等于 0,所以 ∫ − ∞ + ∞ x sin x x 2 + 16 d x = 0 \int_{-\infty}^{+\infty}\frac{x\sin x}{x^2+16}\mathrm{d}x=0 ∫−∞+∞x2+16xsinxdx=0,完毕(这不是很简单?)。
答案
好做完了,然后上网搜一下答案:
x
2
+
16
=
0
x
2
=
−
16
x
=
±
−
16
=
±
4
i
J
=
∮
C
z
e
i
z
z
2
+
16
d
z
=
2
π
i
⋅
z
e
i
z
2
z
∣
z
=
4
i
=
π
i
⋅
e
i
⋅
4
i
=
i
π
e
−
4
∴
∫
−
∞
∞
x
sin
x
x
2
+
16
d
x
=
I
m
(
J
)
=
π
e
−
4
\begin{align*} & x^2+16=0\\ & x^2=-16\\ & x=\pm\sqrt{-16}=\pm4i\\ & J=\oint_C\frac{ze^{iz}}{z^2+16}\mathrm{d}z=2\pi i\cdot\frac{ze^{iz}}{2z}\Big|_{z=4i}=\pi i\cdot e^{i\cdot4i}=i\pi e^{-4}\\ & \therefore\int_{-\infty}^\infty\frac{x\sin x}{x^2+16}\mathrm{d}x=\mathrm{Im}(J)=\pi e^{-4} \end{align*}
x2+16=0x2=−16x=±−16=±4iJ=∮Cz2+16zeizdz=2πi⋅2zzeiz
z=4i=πi⋅ei⋅4i=iπe−4∴∫−∞∞x2+16xsinxdx=Im(J)=πe−4
啊?怎么不是 0?看到答案后脑子里冒出一个又一个问题:
- 为什么要求分母满足 x 2 + 16 = 0 x^2+16=0 x2+16=0 的解?
- 为什么一个一元函数的积分可以转化成曲线积分?曲线积分不是在平面上才有的吗?
- z z z 跟 x x x 是什么关系? x sin x = z e i z x\sin x=ze^{iz} xsinx=zeiz 吗?
- 2 π i 2\pi i 2πi 是从哪里来的?
- z e i z 2 z \frac{ze^{iz}}{2z} 2zzeiz 分母的那个 2 z 2z 2z 又是什么东西?
- 为什么只取 z = 4 i z=4i z=4i 的值代入计算, z = − 4 i z=-4i z=−4i 直接扔掉了?
- 最后那个 I m ( J ) \mathrm{Im}(J) Im(J) 里 I m \mathrm{Im} Im 又是什么函数?
总之是没有一步是看得懂的,这真的是刚学完高数能做的积分吗?
答案不等于
0
0
0 说明这不是一个奇函数,先画个图看一看:
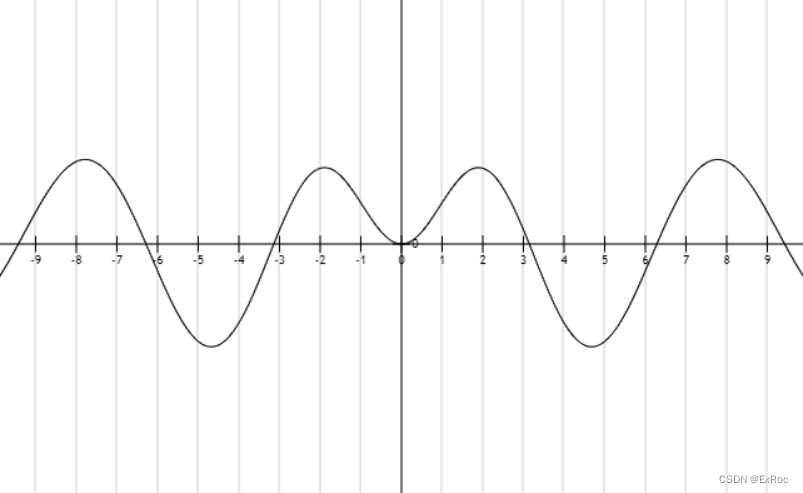
怎么是个偶函数?噢对不起,奇函数乘上奇函数是一个偶函数,大错特错嘞。上网搜搜,解这题需要用到什么知识点,搜到了 B 站视频:合集·高等数学(物理类专业用-四川大学编),看起来是要用到留数定理,开学!
以下为看懂本题答案需要的所有前置知识(除高数以外)(不,其实是我个人的学习笔记)。
本文中略的部分可能属于以下几种情况之一:
- 太简单
- 高数书的旧知识
- 跟本题无关
- 证明太繁琐,仅给出思路
留数定理,启动!
1.1 复数
1.1.1 复数域
复数:形如 z = x + i y z=x+iy z=x+iy 的数,其中 x , y ∈ R x,y\in R x,y∈R, i i i 为虚数单位( i 2 = − 1 i^2=-1 i2=−1),称 x x x 为 z z z 的实部,记 x = R e ( z ) x=\mathrm{Re}(z) x=Re(z), y y y 为 z z z 的虚部,记 y = I m ( z ) y=\mathrm{Im}(z) y=Im(z),基本运算规则略(仅为说明答案中 I m \mathrm{Im} Im 的含义)。
1.1.2 复平面
如下图建立平面直角坐标系,横坐标为实轴,纵坐标为虚轴,则 z = x + i y z=x+iy z=x+iy 可以在平面上唯一确定一点,从 ( 0 , 0 ) (0,0) (0,0) 指向 ( x , y ) (x,y) (x,y) 的有向线段可表示为一条向量,借鉴向量的含义,复数的模表示为 r = ∣ z ∣ r=|z| r=∣z∣,幅角表示为 A r g ( z ) = θ + 2 k π ( k ∈ Z ) \mathrm{Arg}(z)=\theta+2k\pi(k\in Z) Arg(z)=θ+2kπ(k∈Z),复数的幅角不唯一,一般将 ( − π , π ] (-\pi,\pi] (−π,π] 或 [ 0 , 2 π ) [0,2\pi) [0,2π) 的幅角称为 A r g ( z ) \mathrm{Arg}(z) Arg(z) 的主值,记为 a r g ( z ) = θ \mathrm{arg}(z)=\theta arg(z)=θ,该平面称为复平面。
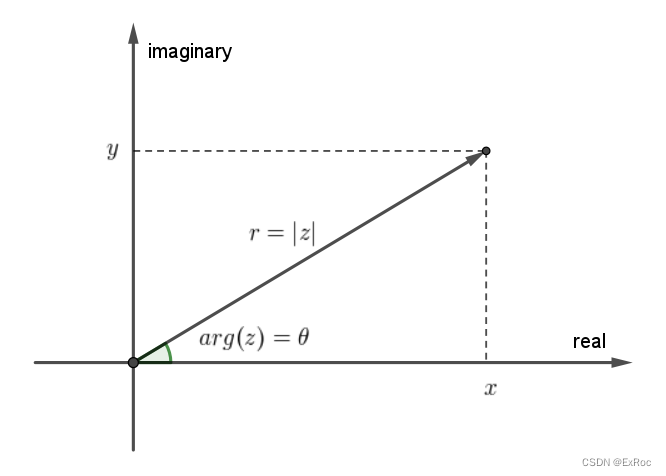
由图可得: z = x + i y = r ( cos θ + i sin θ ) = r e i θ z=x+iy=r(\cos\theta+i\sin\theta)=re^{i\theta} z=x+iy=r(cosθ+isinθ)=reiθ,表示模长为 r r r 的向量从实轴开始逆时针旋转 θ \theta θ 角得到的向量所代表的复数为 z = x + i y z=x+iy z=x+iy。
特别地, e i π = − 1 ⟺ e i π + 1 = 0 e^{i\pi}=-1\iff e^{i\pi}+1=0 eiπ=−1⟺eiπ+1=0, 0 0 0、 1 1 1(来自算术), π \pi π(来自几何), e e e(来自分析学), i i i(来自代数)这五个数以及加法、乘法、指数运算这 3 种重要的数学运算巧妙的结合在一起,优美,太优美了!
其中 cos θ + i sin θ = e i θ \cos\theta+i\sin\theta=e^{i\theta} cosθ+isinθ=eiθ 为欧拉公式,证略;由复数的指数形式推导模长、幅角计算公式略。
1.1.3 复数的乘幂与方根(略)
感兴趣可以学习视频:【官方双语】欧拉公式与初等群论,从另一个角度理解复数域的运算(本节与答案无关)
1.2 复变函数
1.2.1 区域与若尔当曲线(略)
本节是对复数在复平面上的拓扑概念的严格数学定义,后面看到这些概念其实可以自然理解。
1.2.2 复变函数的概念
概念、定义内容略。
过渡内容:对于复数 z = x + i y z=x+iy z=x+iy, f ( z ) f(z) f(z) 总能表示为 u ( x , y ) + i v ( x , y ) u(x,y)+iv(x,y) u(x,y)+iv(x,y) 的形式,其中 u ( x , y ) , v ( x , y ) u(x,y),v(x,y) u(x,y),v(x,y) 均为实函数,后面对于复变函数的研究总可以从二元函数角度出发进行。
1.2.3 极限与连续(略)
本节使用 ε δ \varepsilon~\delta ε δ 语言严格定义复变函数的极限与连续,与实函数类似。
利用 f ( z ) = u ( x , y ) + i v ( x , y ) f(z)=u(x,y)+iv(x,y) f(z)=u(x,y)+iv(x,y) 可将复变函数的极限、连续性问题转化为实二元函数的类似问题,相关公式、定理略。
注:由于复数不能比较大小,复变函数的连续性与有界性表现为函数值模的连续性与有界性。
2.1 解析函数的概念与柯西·黎曼条件
2.1.1 导数与微分
导数定义:设 w = f ( z ) w=f(z) w=f(z) 在区域 D D D 内有定义。若点 z ∈ D z\in D z∈D 有 lim Δ z → 0 Δ w Δ z = lim Δ z → 0 f ( z + Δ z ) − f ( z ) Δ z \lim_{\Delta z\rightarrow0}\frac{\Delta w}{\Delta z}=\lim_{\Delta z\rightarrow0}\frac{f(z+\Delta z)-f(z)}{\Delta z} limΔz→0ΔzΔw=limΔz→0Δzf(z+Δz)−f(z) 存在,则称 f ( z ) f(z) f(z) 在 z z z 点可导,此极限称为 f ( z ) f(z) f(z) 在 z z z 点的导数,记为 f ′ ( z ) f'(z) f′(z)。
微分定义:如果
w
=
f
(
z
)
w=f(z)
w=f(z) 在点
z
∈
D
z\in D
z∈D 处的改变量
Δ
w
=
f
(
z
+
Δ
z
)
−
f
(
z
)
\Delta w=f(z+\Delta z)-f(z)
Δw=f(z+Δz)−f(z) 可写成
Δ
w
=
A
(
z
)
⋅
Δ
z
+
ρ
(
Δ
z
)
\Delta w=A(z)\cdot\Delta z+\rho(\Delta z)
Δw=A(z)⋅Δz+ρ(Δz) 的形式,则称
f
(
z
)
f(z)
f(z) 在
z
z
z 点可微。线性部分
A
(
z
)
⋅
Δ
z
A(z)\cdot\Delta z
A(z)⋅Δz 称为
f
(
z
)
f(z)
f(z) 在
z
z
z 处的微分,记作
d
w
=
d
f
=
A
(
z
)
d
z
dw=df=A(z)dz
dw=df=A(z)dz。
其中
ρ
(
Δ
z
)
\rho(\Delta z)
ρ(Δz) 满足
lim
Δ
z
→
0
ρ
(
Δ
z
)
Δ
z
=
0
\lim_{\Delta z\rightarrow0}\frac{\rho(\Delta z)}{\Delta z}=0
limΔz→0Δzρ(Δz)=0,即
ρ
(
Δ
z
)
\rho(\Delta z)
ρ(Δz) 是关于
Δ
z
\Delta z
Δz 的复变函数,且它是
Δ
z
\Delta z
Δz 的高阶无穷小。
- 注 1:复变函数可导等价于可微,证略。
- 注 2:在实函数中, Δ x \Delta x Δx 指分别从 − ∞ -\infty −∞ 或者 + ∞ +\infty +∞ 两个方向趋于 x x x 做差,在复变函数中 Δ z \Delta z Δz 指从复平面上任意方向趋于 z z z 做差。
- 注 3:复变函数对应的每个实二元函数 u ( x , y ) , v ( x , y ) u(x,y),v(x,y) u(x,y),v(x,y) 都可微,该复变函数不一定可微。反例: f ( z ) = z ˉ f(z)=\bar{z} f(z)=zˉ,由于与答案无关,证略。
求导公式略。
2.1.2 柯西·黎曼条件
若复变函数 f ( z ) = u ( x , y ) + i v ( x , y ) f(z)=u(x,y)+iv(x,y) f(z)=u(x,y)+iv(x,y) 可微,则满足 ∂ u ∂ x = ∂ v ∂ y \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} ∂x∂u=∂y∂v 且 ∂ u ∂ y = − ∂ v x \frac{\partial u}{\partial y}=-\frac{\partial v}{x} ∂y∂u=−x∂v(柯西·黎曼条件,也称 C-R 条件)。
证明思路:将 u , v u,v u,v 代入导数的定义: f ′ ( z ) = lim Δ z → 0 f ( z + Δ z ) − f ( z ) Δ z f'(z)=\lim_{\Delta z\rightarrow0}\frac{f(z+\Delta z)-f(z)}{\Delta z} f′(z)=limΔz→0Δzf(z+Δz)−f(z),分别从实轴正方向与虚轴正方向趋近 0 0 0 得到的极限应该相等,得到 f ( z ) = ∂ u ∂ x + i ∂ v ∂ x = ∂ v ∂ y − i ∂ u ∂ y f(z)=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}=\frac{\partial v}{\partial y}-i\frac{\partial u}{\partial y} f(z)=∂x∂u+i∂x∂v=∂y∂v−i∂y∂u。
f ( z ) = u ( x , y ) + i v ( x , y ) f(z)=u(x,y)+iv(x,y) f(z)=u(x,y)+iv(x,y) 在区域 D D D 内有定义, f ( z ) f(z) f(z) 在点 z = x + i y z=x+iy z=x+iy 处可微的充要条件为: u ( x , y ) , v ( x , y ) u(x,y),v(x,y) u(x,y),v(x,y) 在 ( x , y ) (x,y) (x,y) 处可微,并且 u x = v y , u y = − v x u_x=v_y,u_y=-v_x ux=vy,uy=−vx( u x u_x ux 表示 ∂ u ∂ x \frac{\partial u}{\partial x} ∂x∂u,其他符号同理)
证明思路:
- 必要性:由
f
(
z
)
f(z)
f(z) 可微得
Δ
f
(
z
)
=
A
(
z
)
⋅
Δ
z
+
ρ
(
Δ
z
)
\Delta f(z)=A(z)\cdot\Delta z+\rho(\Delta z)
Δf(z)=A(z)⋅Δz+ρ(Δz),设
A
(
z
)
=
a
+
b
i
A(z)=a+bi
A(z)=a+bi,另外可将
Δ
f
(
z
)
=
f
(
z
+
Δ
z
)
−
f
(
z
)
\Delta f(z)=f(z+\Delta z)-f(z)
Δf(z)=f(z+Δz)−f(z) 拆解为关于
u
(
x
,
y
)
,
v
(
x
,
y
)
u(x,y),v(x,y)
u(x,y),v(x,y) 的函数,拆解后实部虚部分别相等,可得
{ u ( x + Δ x , y + Δ y ) − u ( x , y ) = a Δ x − b Δ y + R e ( ρ ( Δ z ) ) v ( x + Δ x , y + Δ y ) − v ( x , y ) = b Δ x + a Δ y + I m ( ρ ( Δ z ) ) \begin{equation} \begin{cases} u(x+\Delta x,y+\Delta y)-u(x,y)=a\Delta x-b\Delta y+\mathrm{Re}(\rho(\Delta z)) \\ v(x+\Delta x,y+\Delta y)-v(x,y)=b\Delta x+a\Delta y+\mathrm{Im}(\rho(\Delta z)) \end{cases} \end{equation} {u(x+Δx,y+Δy)−u(x,y)=aΔx−bΔy+Re(ρ(Δz))v(x+Δx,y+Δy)−v(x,y)=bΔx+aΔy+Im(ρ(Δz))
只需要证明 R e ( ρ ( Δ z ) ) \mathrm{Re}(\rho(\Delta z)) Re(ρ(Δz)) 与 I m ( ρ ( Δ z ) ) \mathrm{Im}(\rho(\Delta z)) Im(ρ(Δz)) 均为 x 2 + y 2 \sqrt{x^2+y^2} x2+y2 的高阶无穷小,即可得到 a = u x = v y , b = − u y = v x a=u_x=v_y,b=-u_y=v_x a=ux=vy,b=−uy=vx,证略。 - 充分性:由 u , v u,v u,v 在 ( x , y ) (x,y) (x,y) 处可微可得式 ( 1 ) (1) (1),其中需要分别将 R e ( ρ ( Δ z ) ) \mathrm{Re}(\rho(\Delta z)) Re(ρ(Δz)) 与 I m ( ρ ( Δ z ) ) \mathrm{Im}(\rho(\Delta z)) Im(ρ(Δz)) 改为 η 1 , η 2 \eta_1,\eta_2 η1,η2,表示为两个二元函数微分后的高阶无穷小量,最后需要证明 η 1 + i η 2 \eta_1+i\eta_2 η1+iη2 是 Δ z \Delta z Δz 的高阶无穷小,即可说明 f ( z ) f(z) f(z) 在 z = x + i y z=x+iy z=x+iy 处可微,证略。
2.1.3 解析函数
解析函数定义: f ( z ) f(z) f(z) 在点 z 0 z_0 z0 的某领域内有定义,且处处可微,则称 z 0 z_0 z0 为 f ( z ) f(z) f(z) 的解析点,或称 f ( z ) f(z) f(z) 在 z 0 z_0 z0 处解析。若 f ( z ) f(z) f(z) 在区域 D D D 内点点解析,则称 f ( z ) f(z) f(z) 在区域 D D D 内解析,称 f ( z ) f(z) f(z) 是 D D D 内的解析函数。
奇点的定义:若 f ( z ) f(z) f(z) 在点 z 0 z_0 z0 不解析,但在 z 0 z_0 z0 的任意邻域内总有 f ( z ) f(z) f(z) 的解析点,则称 z 0 z_0 z0 是 f ( z ) f(z) f(z) 的奇点。
注:解析函数有非常好的光滑性,解析函数在解析点上无限次可微!(证略或者后面再证明)
2.2 解析函数与调和函数的关系(略)
本节内容如题,主要通过解析函数的 C-R 条件 + 可微性质推导其与调和函数的关系,由于与答案无关,略。
2.3 初等解析函数
2.3.1 初等单值函数(重要)
- 幂函数相关:
- 正整数次的幂函数( f ( z ) = z n f(z)=z^n f(z)=zn)在复平面上解析;
- 多项式函数( f ( z ) = ∑ i = 0 n a i z i f(z)=\sum_{i=0}^n a_i z^i f(z)=∑i=0naizi)在复平面上解析;
- 有理函数( f ( z ) = ∑ i = 0 n a i z i ∑ j = 0 m b j z j f(z)=\frac{\sum_{i=0}^n a_i z^i}{\sum_{j=0}^m b_j z^j} f(z)=∑j=0mbjzj∑i=0naizi)在所有满足 ∑ j = 0 m b j z j = 0 \sum_{j=0}^m b_j z^j=0 ∑j=0mbjzj=0 的点上为奇点,在复平面上除奇点外均解析,2.1.2 节的充要条件可证,证略;
- 指数函数( f ( z ) = e z f(z)=e^z f(z)=ez)在复平面上解析,证略;
- 三角函数 cos z = e i z + e − i z 2 \cos z=\frac{e^{iz}+e^{-iz}}{2} cosz=2eiz+e−iz, sin z = e i z − e − i z 2 i \sin z=\frac{e^{iz}-e^{-iz}}{2i} sinz=2ieiz−e−iz(欧拉公式可得)在复平面上解析,证略;
- 相关公式与当 z z z 为纯实数时的形式相同(如 ( z n ) ′ = n z n − 1 , ( e z ) ′ = e z , ( sin z ) ′ = cos z (z^n)'=nz^{n-1},(e^z)'=e^z,(\sin z)'=\cos z (zn)′=nzn−1,(ez)′=ez,(sinz)′=cosz),而领一些与实函数不同的性质由于与答案无关,略;证略;
到这里我们终于可以看懂答案的第一步是在做什么了:由于被积函数 x sin x x 2 + 16 \frac{x\sin x}{x^2+16} x2+16xsinx 中分子在复平面上解析,分母是一个有理函数,因此求分母满足 x 2 + 16 = 0 x^2+16=0 x2+16=0 的解,即找出被积函数在复平面上的奇点(这里变量为 x x x 或者 z z z 并无区别),之后围绕奇点做一些计算。
搞懂了第一步在算奇点,但还不知道为什么要算这个奇点,所以只能算是向成功迈出了 0.5 步吧(终于有进展了,泪目/(ㄒoㄒ)/~~)
2.3.2 初等多值函数
复数幅角的多值性导致复数函数的多值性(如函数 f ( z ) = z 1 3 f(z)=z^{\frac{1}{3}} f(z)=z31 当自变量 z = − 1 z=-1 z=−1 时,因变量可以为 e i π + 2 k π 3 , k ∈ Z e^{i\frac{\pi+2k\pi}{3}},k\in Z ei3π+2kπ,k∈Z),对于多值函数无法讨论在某一点上的解析、可微等性质,因此本节引入单值分支的概念限制值域、支割线的概念限制定义域,将多值函数限制在单值函数中,再进行后续内容的学习。
3.1 复积分的概念与性质
3.1.1 定义
设 C C C 是一条以 z 0 z_0 z0 为起点, z ′ z' z′ 为终点的有向曲线,函数 f ( z ) f(z) f(z) 在 C C C 上有定义。沿着 C C C 的正向依次取 z 0 , z 1 , ⋯ , z n = z ′ z_0,z_1,\cdots,z_n=z' z0,z1,⋯,zn=z′,考虑 ∑ i = 1 n f ( ξ i ) Δ z i \sum_{i=1}^nf(\xi_i)\Delta z_i ∑i=1nf(ξi)Δzi,其中 Δ z i = z i − z i − 1 \Delta z_i=z_i-z_{i-1} Δzi=zi−zi−1, ξ i \xi_i ξi 为弧段 z i − 1 z i ⌢ \overset{\LARGE{\frown}}{z_{i-1}z_i} zi−1zi⌢ 上的一点。
设 λ = max 1 ≤ i ≤ n { ∣ Δ z i ∣ } \lambda=\max_{1\leq i\leq n}\{|\Delta z_i|\} λ=max1≤i≤n{∣Δzi∣},若极限 lim λ → 0 ∑ i = 1 n f ( ξ i ) Δ z i \lim_{\lambda\to0}\sum_{i=1}^nf(\xi_i)\Delta z_i limλ→0∑i=1nf(ξi)Δzi 存在,且与划分方式、 ξ i \xi_i ξi 选取方式无关,则称 f ( z ) f(z) f(z) 沿 C C C 可积。
定义 ∫ C f ( z ) d z = lim λ → 0 ∑ i = 1 n f ( ξ i ) Δ z i \int_Cf(z)\mathrm{d}z=\lim_{\lambda\to0}\sum_{i=1}^nf(\xi_i)\Delta z_i ∫Cf(z)dz=limλ→0∑i=1nf(ξi)Δzi 为 f ( z ) f(z) f(z) 沿 C C C 的积分, C C C 称为积分路径。
以上定义方式严谨但不好理解,这里做一些简单的解释以帮助理解这个积分的含义:
假设有一个人在复平面上从 z 0 = ( x 0 , y 0 ) z_0=(x_0,y_0) z0=(x0,y0) 点沿着曲线 C C C 的路径方向走到 z ′ = ( x ′ , y ′ ) z'=(x',y') z′=(x′,y′),在这个过程中他用大小与方向不断变化着的力 F F F 推着一个箱子前进,而这个力 F F F 是关于他所经过路径上的点 z z z 的函数 F = f ( z ) F=f(z) F=f(z),我们知道力在路径上的做功为 W = F s W=Fs W=Fs,当 F F F 为恒力且 s s s 为线段时可简化为直接相乘,而变力作用在曲线路径的情况下,需要将 s s s 细分为无穷多小段 s i s_i si,在其中的每一段 F F F 都是一个关于箱子所在位置的函数,即 W = F s = lim s i → 0 ∑ i = 1 n f ( z i ) s i = ∫ C f ( z ) d z W=Fs=\lim_{s_i\to0}\sum_{i=1}^n f(z_i)s_i=\int_Cf(z)\mathrm{d}z W=Fs=limsi→0∑i=1nf(zi)si=∫Cf(z)dz,在这里积分的结果就是变力 F F F 沿着曲线路径 C C C 所做的功。
注意:这里用一个复数 z = x + i y z=x+iy z=x+iy 表示在平面上的位置,而用另一个复数 f ( z ) f(z) f(z) 表示力的大小与方向(向量)。
注 1:简单闭曲线的正向(下图可帮助理解):
- 面朝正向,左手指向内部,右手指向外部(二维平面适用)
- 外法向为 x x x 轴方向,正向为 y y y 轴方向(可拓展至高维空间)
注 2:积分路径不同,积分值可能不同,例:积分 ∫ C R e ( z ) d z \int_C\mathrm{Re}(z)\mathrm{d}z ∫CRe(z)dz,沿着以下两条路径积分值不同
- C C C 为链接 0 0 0 与 1 + i 1+i 1+i 的直线段,积分值为 1 + i 2 \frac{1+i}{2} 21+i
- C C C 为链接 0 0 0 与 1 1 1, 1 1 1 与 1 + i 1+i 1+i 的折线段,积分值为 1 2 + i \frac{1}{2}+i 21+i
TODO: 补充一张图,参考 013 节板书
若能将 z z z 写成关于 t t t 的参数方程 z = z ( t ) z=z(t) z=z(t),则 ∫ C f ( z ) d z = ∫ α β f ( z ( t ) ) z ′ ( t ) d t \int_Cf(z)\mathrm{d}z=\int_\alpha^\beta f(z(t))z'(t)\mathrm{d}t ∫Cf(z)dz=∫αβf(z(t))z′(t)dt,推导略。
★★★ 计算以下积分,曲线 C C C 为以 a a a 为中心, ρ ( ρ > 0 ) \rho(\rho>0) ρ(ρ>0) 为半径的圆周(非常非常重要):
I = ∮ C d z ( z − a ) n = { 2 π i , 当 n = 1 时 0 , 当 n ≠ 1 且 n 为整数时 I=\oint_C\frac{\mathrm{d}z}{(z-a)^n}=\begin{equation} \begin{cases} 2\pi i, &\text{当} n=1 \text{时}\\ 0, &\text{当} n\neq1\text{且 n 为整数时} \end{cases} \end{equation} I=∮C(z−a)ndz={2πi,0,当n=1时当n=1且 n 为整数时
考虑 z ∈ C z\in C z∈C,设 z ( θ ) = a + ρ e i θ , θ ∈ [ 0 , 2 π ) z(\theta)=a+\rho e^{i\theta},\theta\in[0,2\pi) z(θ)=a+ρeiθ,θ∈[0,2π),则 d z = i ρ e i θ d θ \mathrm{d}z=i\rho e^{i\theta}\mathrm{d}\theta dz=iρeiθdθ
I = ∮ C d z ( z − a ) n = ∫ 0 2 π i ρ e i θ d θ ( a + ρ e i θ − a ) n = ∫ 0 2 π i ρ e i θ ρ n e i n θ d θ = i ρ 1 − n e i θ ( 1 − n ) ∣ 0 2 π \begin{equation} \begin{split} I &= \oint_C\frac{\mathrm{d}z}{(z-a)^n} \\ &= \int_0^{2\pi}\frac{i\rho e^{i\theta}\mathrm{d}\theta}{(a+\rho e^{i\theta}-a)^n} \\ &= \int_0^{2\pi}\frac{i\rho e^{i\theta}}{\rho^n e^{in\theta}}\mathrm{d}\theta \\ &= i\rho^{1-n}e^{i\theta(1-n)}\bigg|_0^{2\pi} \notag \end{split} \end{equation} I=∮C(z−a)ndz=∫02π(a+ρeiθ−a)niρeiθdθ=∫02πρneinθiρeiθdθ=iρ1−neiθ(1−n) 02π
当 n = 1 n=1 n=1 时, I = 2 π i I=2\pi i I=2πi,当 n ≠ 1 n\neq1 n=1 且 n n n 为整数时:
I = i ρ 1 − n ( e 2 π i ( 1 − n ) − 1 ) = i ρ 1 − n ( cos ( 2 π ( 1 − n ) ) + i sin ( 2 π ( 1 − n ) ) − 1 ) = i ρ 1 − n ( 1 + i × 0 − 1 ) = 0 \begin{equation} \begin{split} I &= i\rho^{1-n}(e^{2\pi i(1-n)}-1)\\ &= i\rho^{1-n}(\cos(2\pi(1-n))+i\sin(2\pi(1-n))-1) \\ &= i\rho^{1-n}(1+i\times0-1) \\ &= 0 \notag \end{split} \end{equation} I=iρ1−n(e2πi(1−n)−1)=iρ1−n(cos(2π(1−n))+isin(2π(1−n))−1)=iρ1−n(1+i×0−1)=0
到这里回顾一下答案,可以发现已经出现了答案中 ∮ C f ( z ) d z = 2 π i g ( z ) ∣ z = 4 i \oint_C f(z)\mathrm{d}z=2\pi ig(z)|_{z=4i} ∮Cf(z)dz=2πig(z)∣z=4i 这一行的部分关键内容。我们大胆猜测,这是在 f ( z ) f(z) f(z) 的其中一个奇点 z = 4 i z=4i z=4i 附近找了一条半径任意小的圆形积分路径,对这条路径做积分,但我们仍不清楚这么做的原因是什么。
3.1.2 性质
- ∫ C d z = z n − z 1 \int_C\mathrm{d}z=z_n-z_1 ∫Cdz=zn−z1, z 1 , z n z_1,z_n z1,zn 分别为曲线 C C C 的起点与终点;
- 线性: ∫ C ( a 1 f 1 ( z ) + a 2 f 2 ( z ) ) d z = a 1 ∫ C f 1 ( z ) d z + a 2 ∫ C f 2 ( z ) d z \int_C(a_1f_1(z)+a_2f_2(z))\mathrm{d}z=a_1\int_Cf_1(z)\mathrm{d}z+a_2\int_Cf_2(z)\mathrm{d}z ∫C(a1f1(z)+a2f2(z))dz=a1∫Cf1(z)dz+a2∫Cf2(z)dz,其中 a 1 , a 2 a_1,a_2 a1,a2 为常数;
- 区域可加性: ∫ C f ( z ) d z = ∫ C 1 f ( z ) d z + ∫ C 2 f ( z ) d z \int_Cf(z)\mathrm{d}z=\int_{C_1}f(z)\mathrm{d}z+\int_{C_2}f(z)\mathrm{d}z ∫Cf(z)dz=∫C1f(z)dz+∫C2f(z)dz,其中曲线 C C C 由 C 1 , C 2 C_1,C_2 C1,C2 首尾连接;
- ∫ C f ( z ) d z = ∫ C − f ( z ) d z \int_Cf(z)\mathrm{d}z=\int_{C^-}f(z)\mathrm{d}z ∫Cf(z)dz=∫C−f(z)dz,其中曲线 C − C^- C− 为与 C C C 方向相反的同一曲线;
- ∣ ∫ C f ( z ) d z ∣ ≤ ∫ C ∣ f ( z ) ∣ ∣ d z ∣ = ∫ C ∣ f ( z ) ∣ d s |\int_Cf(z)\mathrm{d}z|\leq\int_C|f(z)||\mathrm{d}z|=\int_C|f(z)|\mathrm{d}s ∣∫Cf(z)dz∣≤∫C∣f(z)∣∣dz∣=∫C∣f(z)∣ds,其中 d s \mathrm{d}s ds 仅表示为曲线的曲线的一小段长度微元;
- 若 ∣ f ( z ) ∣ ≤ M |f(z)|\leq M ∣f(z)∣≤M,曲线 C C C 的长度 ∫ C d s ≤ ρ \int_C\mathrm{d}s\leq\rho ∫Cds≤ρ,则 ∣ ∫ C f ( z ) d z ∣ ≤ ρ M |\int_Cf(z)\mathrm{d}z|\leq\rho M ∣∫Cf(z)dz∣≤ρM





















 6414
6414











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








