简介:在图像处理中,梯度是关键特征,揭示像素强度变化。本文探讨使用MATLAB计算图像梯度,涉及随机梯度算法、相对梯度算法和压缩传感技术。通过 mingsou.m 脚本展示具体应用和理论实现。 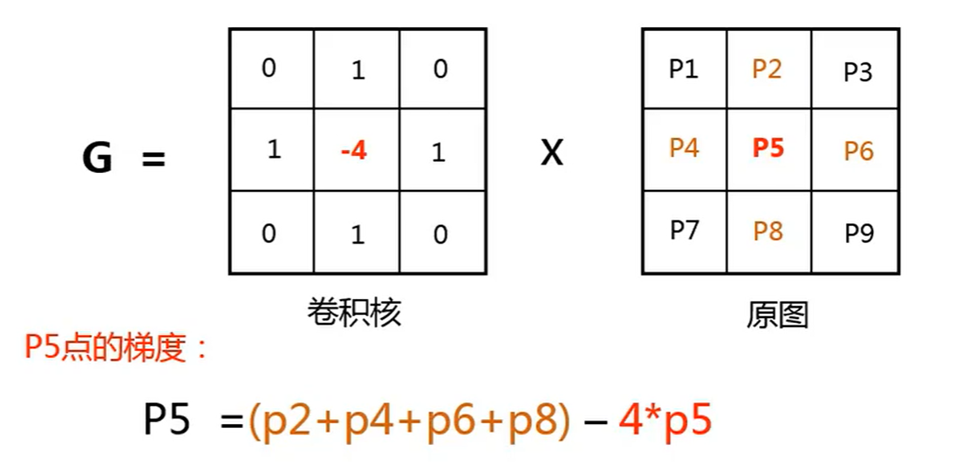
1. 图像梯度的基本概念和重要性
图像梯度是图像处理中的基础概念,它描述了图像强度在空间上的变化率。理解图像梯度对于图像分析、特征提取、边缘检测和许多其他图像处理任务至关重要。图像梯度的方向通常指向图像亮度变化最快的方向,而梯度的幅度则表示变化的速度。在许多图像处理算法中,梯度信息是用于进一步分析和决策的基础,如在边缘检测算法中,边缘通常对应于图像梯度的局部最大值。理解图像梯度的原理及其在图像处理中的应用,对于提高图像分析的质量和效率具有举足轻重的作用。接下来,我们将探索MATLAB中图像梯度的计算方法及其内置函数的使用,以便更好地进行图像处理和分析。
2. MATLAB中计算图像梯度的方法与内置函数
MATLAB为图像处理提供了强大的工具箱,其中内置了多种计算图像梯度的函数。图像梯度是图像处理中的重要概念,它反映了图像的局部亮度变化,对于边缘检测、图像增强、特征提取等应用至关重要。本章节将介绍图像梯度的数学基础,并深入探讨MATLAB中计算图像梯度的方法和内置函数。
2.1 图像梯度的数学基础
2.1.1 梯度的定义和性质
在数学中,梯度是一个向量,指向函数增长最快的方向。对于二维函数f(x, y),梯度定义为:
∇f = (∂f/∂x, ∂f/∂y)
其中,∂f/∂x和∂f/∂y分别是函数f关于x和y的偏导数。在图像处理中,我们将图像视为定义在二维空间上的函数,其梯度则对应于每个像素点的亮度变化。
梯度向量的大小(模):
||∇f|| = √[(∂f/∂x)² + (∂f/∂y)²]
表示图像在该点的边缘强度,方向则指向亮度变化最大的方向。
2.1.2 图像梯度的离散化处理
在实际数字图像处理中,我们处理的是离散像素值。因此,需要对连续的梯度定义进行离散化处理。例如,通过中心差分法:
Gx(x, y) ≈ f(x+1, y) - f(x-1, y)
Gy(x, y) ≈ f(x, y+1) - f(x, y-1)
其中,Gx和Gy分别表示图像沿x轴和y轴的梯度分量。我们常用Sobel算子和Prewitt算子来进行这一操作。
2.2 MATLAB内置图像处理函数
MATLAB提供了多种内置函数来计算图像的梯度,这些函数封装了梯度计算的复杂性,使得用户可以方便快捷地进行图像处理。
2.2.1 Sobel算子和Prewitt算子
Sobel算子是一种用于边缘检测的离散微分算子,它结合了高斯平滑和微分求导。其算子核如下:
Sobel算子核:
Gx = [-1 0 1
-2 0 2
-1 0 1]
Gy = [-1 -2 -1
0 0 0
1 2 1]
而Prewitt算子与Sobel算子类似,但不包含高斯平滑,其核为:
Prewitt算子核:
Gx = [-1 0 1
-1 0 1
-1 0 1]
Gy = [-1 -1 -1
0 0 0
1 1 1]
在MATLAB中,可以使用 fspecial 函数创建Sobel算子:
sobelOperator = fspecial('sobel');
然后使用 imfilter 函数进行滤波,得到图像梯度的近似值。
2.2.2 高级梯度算法如Canny边缘检测
Canny边缘检测算子是图像处理中一种更为高级的边缘检测方法,它包括了对噪声的滤除、寻找强度梯度最强的位置等步骤,以确定图像的边缘。
MATLAB提供 edge 函数来实现Canny边缘检测,其用法如下:
BW = edge(I, 'canny');
其中, I 是输入的灰度图像, BW 是输出的二值边缘图像。
2.2.3 MATLAB内置函数的使用示例
以下是一个简单的MATLAB脚本示例,展示如何使用内置函数来计算图像的梯度。
% 读取图像
I = imread('example.jpg');
I_gray = rgb2gray(I); % 转换为灰度图像
% 计算Sobel算子梯度
sobelOperator = fspecial('sobel');
Gx_sobel = imfilter(double(I_gray), sobelOperator, 'replicate');
Gy_sobel = imfilter(double(I_gray), sobelOperator', 'replicate');
% 计算梯度幅值
gradient_magnitude = sqrt(Gx_sobel.^2 + Gy_sobel.^2);
% 显示梯度幅值图像
figure, imshow(gradient_magnitude, [], 'InitialMagnification', 'fit');
title('Sobel Gradient Magnitude');
% 使用Canny算子进行边缘检测
BW_canny = edge(I_gray, 'canny');
figure, imshow(BW_canny);
title('Canny Edge Detection');
通过上述代码,可以对比使用Sobel算子和Canny算子处理同一图像后得到的梯度幅值和边缘检测结果。
本章节介绍了图像梯度的数学基础,并详细探讨了在MATLAB中计算图像梯度的内置函数。下一章节将介绍随机梯度算法和相对梯度算法,以及它们在MATLAB中的实现方式。
3. 随机梯度算法和相对梯度算法的介绍与MATLAB实现
3.1 随机梯度算法的原理和应用
3.1.1 随机梯度下降算法的简介
随机梯度下降(Stochastic Gradient Descent, SGD)是机器学习中用于优化问题的一种常用算法,它通过逐个或一小批样本计算损失函数的梯度,从而更新模型参数。与传统的梯度下降相比,随机梯度下降能够快速收敛,并且在大数据集上实现高效的参数更新,而不需要在整个数据集上计算梯度。
随机梯度下降的核心思想是使用单个样本(或一小批样本)产生的梯度来近似整个数据集的梯度。尽管这种近似可能不完全准确,但在许多实际情况下,它大大减少了计算量,并且可以获得快速收敛到局部最优解的结果。
3.1.2 随机梯度在图像处理中的应用案例
在图像处理中,随机梯度算法可以应用于各种优化问题,如图像分割、图像分类等。特别地,在深度学习用于图像处理的背景下,随机梯度下降经常与神经网络配合使用,用于训练网络参数。例如,卷积神经网络(Convolutional Neural Networks, CNNs)在处理图像识别任务时,常常采用随机梯度下降作为优化器。
以下是一个使用MATLAB实现随机梯度下降算法进行图像处理的简单示例:
% 假设我们有一个简单的线性模型 w*x + b,目标是最小化平方损失函数
% X为输入特征,Y为对应的目标值
% 初始化参数
w = 0;
b = 0;
X = rand(100, 1) * 10; % 随机生成100个样本特征
Y = 3 * X + 2 + randn(100, 1); % 随机生成100个样本目标值
% 学习率和迭代次数
learning_rate = 0.01;
num_iterations = 100;
% 随机梯度下降优化过程
for i = 1:num_iterations
idx = randperm(size(X, 1)); % 随机打乱数据集索引
for j = 1:size(X, 1)
x = X(idx(j));
y = Y(idx(j));
% 计算梯度
gradient_w = (w*x + b - y) * x;
gradient_b = w*x + b - y;
% 更新参数
w = w - learning_rate * gradient_w;
b = b - learning_rate * gradient_b;
end
end
% 输出最终参数
fprintf('Optimized parameters: w = %f, b = %f\n', w, b);
在上述代码中,我们初始化了模型参数w和b,并生成了随机的特征X和目标值Y。通过迭代,每次随机选择一个样本并计算损失函数的梯度,然后更新参数以最小化损失。代码中每个参数更新步骤展示了随机梯度下降的核心操作。
3.2 相对梯度算法的原理和应用
3.2.1 相对梯度算法的简介
相对梯度算法,也称为共轭梯度法(Conjugate Gradient, CG),是一种用于解决线性方程组和优化问题的迭代方法。在优化问题中,共轭梯度法特别适用于大规模稀疏系统,如图像处理中的各种优化问题。共轭梯度法的优点在于它不需要存储整个Hessian矩阵,而是在每次迭代中只进行矩阵向量乘法运算。
共轭梯度法的基本思想是构建一系列共轭方向,这些方向与之前的搜索方向共轭,即它们满足一定条件,使得在这些方向上进行一维搜索能够保证函数值的下降。共轭方向的选择使得每次迭代的搜索效率最大化,尤其是在高维空间中能够有效避免梯度下降中可能出现的“锯齿”现象。
3.2.2 MATLAB实现相对梯度算法的步骤与方法
在MATLAB中实现相对梯度算法,可以使用内置函数或者自定义算法逻辑。以下是使用MATLAB内置函数 pcg 实现共轭梯度法的示例代码:
% 定义线性系统 A*x = b
A = [3 -1 0 -1 0 0; -1 3 -1 0 -1 0; 0 -1 3 0 0 -1; -1 0 0 3 -1 0; 0 -1 0 -1 3 -1; 0 0 -1 0 -1 3];
b = [1; 2; 3; 4; 5; 6];
% 设置初始猜测解为零向量
x0 = zeros(6, 1);
% 调用pcg函数求解线性系统
[x, flx, ier, relres, iter] = pcg(A, b, 1e-8, 100, x0);
% 输出结果
disp('Solution:');
disp(x);
上述代码中, A 是一个对角占优矩阵, b 是一个非零向量。 pcg 函数用于求解线性方程组 Ax = b 。在使用共轭梯度法时,需要一个合理的初始猜测解,这里我们设置为零向量 x0 。 pcg 函数返回的 x 即为线性方程组的解, flx 表示函数值(残差), ier 表示迭代过程中遇到的异常, relres 表示相对残差, iter 表示实际进行的迭代次数。
通过上述示例,可以看出MATLAB中的共轭梯度法实现简洁、高效,非常适合用于大规模图像处理中涉及的优化问题。共轭梯度法不仅优化了计算效率,还减少了内存消耗,使得在面对大规模图像数据时,优化过程更加灵活和快速。
4. 压缩传感技术在图像处理中的应用
压缩传感技术是近年来图像处理领域的一个重要突破,它基于稀疏信号的表示和非线性重建理论,可以极大地提高信号处理的效率和准确性。本章节将详细介绍压缩传感技术的基本原理、优势以及它在图像处理,特别是在图像梯度计算中的应用。
4.1 压缩传感技术概述
压缩传感技术为传统的信号采样和重建方法带来了革命性的改变。在传统的信号处理方法中,为了保证信号能够被正确重建,通常需要以高于Nyquist频率的速率进行采样,这意味着需要采集大量数据并进行存储与传输。压缩传感技术提出了一种新的理论,即信号可以从远低于Nyquist频率的采样率中被精确地重建,前提是信号是稀疏的或可以被稀疏表示。
4.1.1 压缩传感的基本原理和优势
在图像处理中,一个图像可以看作是一个高维信号,其中绝大部分信息可以认为是冗余的。稀疏信号表示意味着图像可以通过一个稀疏的表示系数和一个稀疏基来描述。压缩传感理论指出,如果信号是稀疏的或者可以被转换成稀疏形式,那么只需要远少于传统采样理论要求的样本数就可以实现精确重建。
压缩传感技术的优势在于以下几个方面:
- 采样率降低 :通过压缩传感技术,可以减少采样数量,从而降低数据采集和存储的成本。
- 高效重建算法 :由于信号的稀疏性,重建算法可以在观测数据很少的情况下得到高精度的结果。
- 抗干扰能力 :在存在噪声的环境下,压缩传感技术也能相对稳定地重建信号。
4.1.2 压缩传感在图像处理中的重要性
在图像处理中,压缩传感技术尤为重要,因为它可以在不牺牲图像质量的情况下,大幅减少数据量。这对于大数据量图像的应用场景(例如医学成像、遥感图像等)来说,具有显著的实际应用价值。此外,压缩传感技术还为实时图像处理和传输提供了可能性,因为它减少了对带宽和处理能力的需求。
4.2 压缩传感在图像梯度计算中的应用
压缩传感技术的一个重要应用是优化图像梯度的计算。图像梯度是图像处理中非常关键的一步,它涉及到图像的边缘检测、特征提取等重要处理过程。通过压缩传感技术,可以在保证计算精度的同时,显著提高梯度计算的效率。
4.2.1 利用压缩传感优化图像梯度计算
在图像梯度计算中,应用压缩传感技术主要可以通过以下两个方面:
- 减少梯度计算的样本量 :通过压缩传感,可以在采样阶段直接减少需要处理的像素数量,从而降低梯度计算的复杂度。
- 增强图像梯度的稀疏性 :压缩传感技术可以用来提取图像中更为关键的梯度信息,这些信息以稀疏的形式表达,可以提高重建和分析的准确性。
4.2.2 实际案例分析
为了更具体地展示压缩传感在图像梯度计算中的应用,我们以一个具体的图像处理任务为例。假设我们有一个需要处理的高分辨率医学图像,我们希望在不损失过多图像细节的情况下,快速准确地计算出图像的梯度。
. . . 采集压缩传感样本
首先,我们利用压缩传感技术在图像上进行稀疏采样。这可以通过设计一个压缩传感矩阵(通常是一个随机矩阵)和应用到图像上完成。设计的压缩传感矩阵能够保证图像的稀疏表示,同时又能够用少量样本捕捉图像的最重要信息。
% 假设原始图像为I,这里使用一个简单的随机采样矩阵作为示例
M = randn(sparseSize, imageSize); % 创建一个随机采样矩阵
y = M * I(:); % 压缩传感采样
在上述代码中, sparseSize 是稀疏采样后得到的样本数量, imageSize 是原始图像的像素数量。这段代码展示了如何进行压缩传感采样。
. . . 优化梯度计算
采样完成后,我们需要对采样数据进行处理以计算梯度。这时可以使用一些优化算法,例如基于l1范数的优化,来从稀疏样本中重建图像梯度。
% 假设已知采样矩阵M和采样数据y,使用l1范数优化求解梯度
% 这里仅提供概念代码,实际实现将涉及复杂的优化算法
梯度估计 = l1范数优化(M, y);
上述代码中, l1范数优化 是一种重建算法,它的目标是最小化重建梯度的l1范数,这有利于得到稀疏解。
通过对压缩传感技术的利用,我们可以得到一个计算上更加高效,同时在图像细节上不逊色于传统方法的梯度结果。这种方法在处理大量图像数据时,尤其能够体现其优势。
. . . 案例总结
在实际应用中,压缩传感技术不仅能够提高图像处理的速度,还能在一定程度上提升图像质量。它为图像梯度计算提供了一种新的视角,即利用稀疏性进行高效的数据处理。这一技术在医疗成像、卫星遥感、图像压缩等多个领域都展现出巨大的潜力和应用前景。
通过本章节的探讨,可以看出压缩传感技术在图像处理,尤其是图像梯度计算中的重要性和实际应用价值。它通过其独有的信号处理方法,为图像处理领域带来了一种新的优化途径,极大地拓展了图像处理技术的应用范围和效率。
5. mingsou.m MATLAB脚本的功能与实现细节
5.1 mingsou.m 脚本的功能介绍
5.1.1 脚本的主要功能和设计目标
mingsou.m 是一个强大的MATLAB脚本,旨在为图像处理提供一个高效、直观的梯度计算工具。其设计目标是通过简化梯度计算和边缘检测的复杂性来加速图像分析和处理工作流程。该脚本支持多种梯度算法,包括但不限于Sobel、Prewitt以及更高级的算法,如Canny边缘检测。
5.1.2 脚本在图像梯度计算中的作用
在图像分析中,梯度计算常被用于边缘检测、图像特征提取等关键步骤。 mingsou.m 脚本能够辅助用户快速获取图像的梯度信息,并以直观的形式展现结果。通过减少复杂的手动操作和算法调优需求,使得用户可以专注于结果分析而不是实现细节。
5.2 mingsou.m 脚本的实现细节
5.2.1 脚本内部算法逻辑解析
脚本核心依赖于MATLAB的内置图像处理工具箱函数,如 fspecial 、 edge 等,来执行图像的滤波、边缘检测和梯度计算。 mingsou.m 内部算法逻辑如下:
- 读取用户输入的图像文件。
- 使用预设的滤波器模板(如Sobel或Prewitt算子)进行卷积。
- 应用边缘检测算法(例如Canny方法)来识别图像中的边缘。
- 输出梯度图像以及边缘检测结果。
为了使过程更清晰,以下是 mingsou.m 的一个简化的代码示例:
function [gradient_image, edges] = mingsou(image_path)
% 读取图像
img = imread(image_path);
img = rgb2gray(img); % 转换为灰度图像,如果需要
% 计算梯度
[Gx, Gy] = imgradient(img); % 使用图像处理工具箱的imgradient函数
% 绘制梯度幅值图
gradient_image = sqrt(Gx.^2 + Gy.^2);
% 边缘检测
edges = edge(img, 'Canny');
end
5.2.2 用户如何运行和使用该脚本
用户可以将 mingsou.m 保存到MATLAB的路径下的一个目录中。之后,在MATLAB命令窗口中输入 mingsou('path_to_image.jpg') 即可运行该脚本。脚本将返回计算出的梯度图像和边缘检测结果,可以直接使用 imshow 函数展示:
img_gradient = mingsou('path_to_image.jpg');
imshow(img_gradient);
5.2.3 脚本的优化和错误处理机制
为了提高脚本的健壮性,脚本中包含了一些错误检查和处理机制,例如:
- 在读取图像之前检查文件是否存在。
- 检查输入图像是否为有效的图像格式。
- 对于无法识别的边缘检测方法或算法参数,给出清晰的错误提示。
以下是如何在脚本中实现错误检查的示例:
if ~exist(image_path, 'file')
error('File does not exist: %s', image_path);
end
[img, map] = imread(image_path);
if isempty(img)
error('Failed to read the image file.');
end
通过这样的实现,用户在运行 mingsou.m 时能够获得准确的反馈信息,从而更容易地定位和解决问题。
以上内容为 mingsou.m MATLAB脚本功能与实现细节的简要介绍。脚本作为一个实用工具,大大简化了图像梯度的计算流程,并提供了一个高效、可靠的图像处理解决方案。
简介:在图像处理中,梯度是关键特征,揭示像素强度变化。本文探讨使用MATLAB计算图像梯度,涉及随机梯度算法、相对梯度算法和压缩传感技术。通过 mingsou.m 脚本展示具体应用和理论实现。
























 1151
1151

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








