摄像机几何2

目录

1、世界坐标系

2、摄像机外参数（世界坐标系->相机坐标系）

3、完整相机模型参数含义

3.1、各个符号的物理意义及其维度分别是什么

3.2、投影矩阵M有多少个自由度

3.3、P`转换为欧式坐标如何写

4、定理

5、投影变换的性质

---

1、世界坐标系

        摄像机坐标系描述三维物体的空间信息不太方便，所以引入世界坐标系，将物体从世界坐标系转换到摄像机坐标系。

2、摄像机外参数（世界坐标系->相机坐标系）

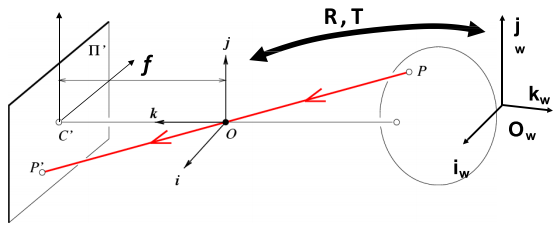
        可以把世界坐标系下的点通过旋转和平移转到摄像机坐标系下，这个转换矩阵就叫相机的外参数。

        R为旋转矩阵（3*3），T为平移矩阵（3*1）,Pw为世界坐标系下的点的齐次坐标（4*1），最终P也为（4*1），物理含义：世界坐标系经过R、T就会得到摄像机坐标系。外参数与摄像机排放的位置有关。

        所以，完整的摄像机模型（世界坐标系下的点—>像素平面坐标系的像素）如下：

3、完整相机模型参数含义

3.1、各个符号的物理意义及其维度分别是什么

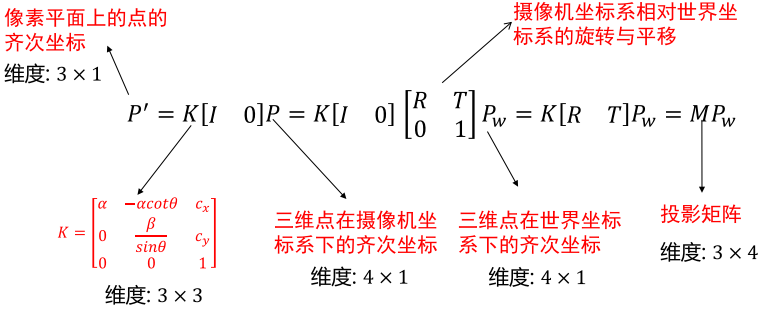
3.2、投影矩阵M有多少个自由度

        外参数，旋转、平移各有3个自由度。最终，投影矩阵M有5+6=11个自由度，简单来说确定了这11个参数，M矩阵就确定了。

3.3、P`转换为欧式坐标如何写

        把M矩阵写成行向量，M是3*4矩阵，m1、m2、m3则为1*4向量，Pw为4*1向量，mi*Pw为实数，除以最后一维，则得欧式坐标。

4、定理

         其中，ai为列向量。叉乘结果垂直于两个向量，点乘为0的向量垂直。

5、投影变换的性质

        1）点投影为点；

        2）线投影为线；

        3）近大远小；

        4）角度不再保持；

        5）平行线相交。