朱利亚 matlab分形图,【分形之美 02】分形图像怎么画？详解曼德勃罗朱利亚分形绘制方法...

原标题：【分形之美 02】分形图像怎么画？详解曼德勃罗朱利亚分形绘制方法

高产猩猩来了，本着坚持不鸽的原则，这两天两更的频率是不是已经破了高产记录？？？

废话不多说直接切入正题，今天咱们来聊聊分形的实现，也就是如何在软件中画出分形~~

这里我会使用虚幻4作为实现的工具，当然你用任何平台和工具都可以，毕竟知道了做法什么软件都是互通的。

在 上一章 中我们科普了分形的基本概念，同时也讲解了曼德勃罗集合和朱利亚集合的算法。理解算法本身很简单，但如果真正涉及到实现的话，会遇到很头疼的问题：

那 就 是 复 数 ！

复数本身其实是由两个维度的数组成，如果我们要在shader中实现复数，就必须将其实部和虚部拆开来算。也就是将二维坐标系中的x对应实部的计算，坐标系y轴的值对应虚数的计算(一般对应的数据就是uv坐标)。

于是我们有了具体思路，那就是将复变函数 Z = Z² + C因式分解，整合成 Z = a + bi的形式。下面我们就来一步步讲解这个变换操作。

一、Z = Z² + C 函数分解

首先我们定义：

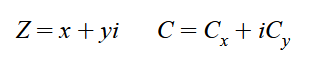
然后分别替换Z = Z² + C中的 Z、C得：

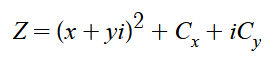
简化一下：

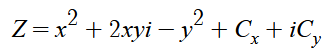
然后我们将Z替换成：

最后简化得：

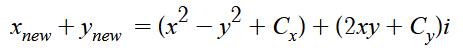
我们将实部和虚部分开，就可以得到下面两个等式：

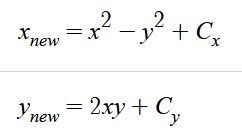
二、曼德勃罗集合实现

公式推出来了，很好，接下来我们就来一步步实现这个效果，打开 ue4 材质编辑器，按照下图所示创建节点，在Custom Node中创建两个变量，其中 n 是循环的次数，C 就是复变函数中的 C ，这里我使用屏幕空间的 uv 作为 C 值输入。

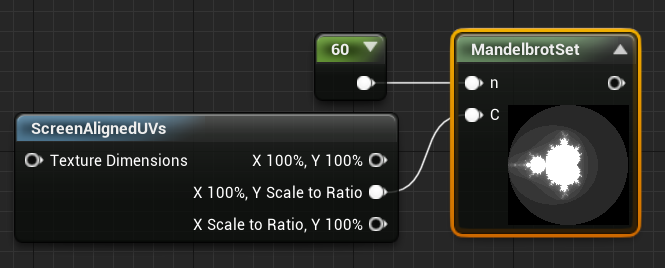
接下来在Custom Node中写入如下代码(不懂看注释)：

// 统一定义一些必要的变量

floatx = 0 , y = 0 , xnew , ynew;

// 将屏幕uv空间缩放至原来的两倍并将0点挪到屏幕中心

C = C * 4 - 2;

// 复变函数循环开始

for (inti = 0; i

{

// 将上面推导出来的公式运用进去

xnew = x*x - y*y + C.x;

ynew = 2*x*y + C.y;

// 判断迭代后复数的长度是否大于2，如果大于就返回他逃离所用的次数与总次数的比值(这里大于4是因为没有算平方根)

if( xnew*xnew + ynew*ynew > 4 ){

return (float)i / (float)n;

}

// 将函数的结果值赋予函数本身迭代计算

x=xnew;

y=ynew;

}

// 循环完成返回最大次数值(其实可以是1)

return(n);

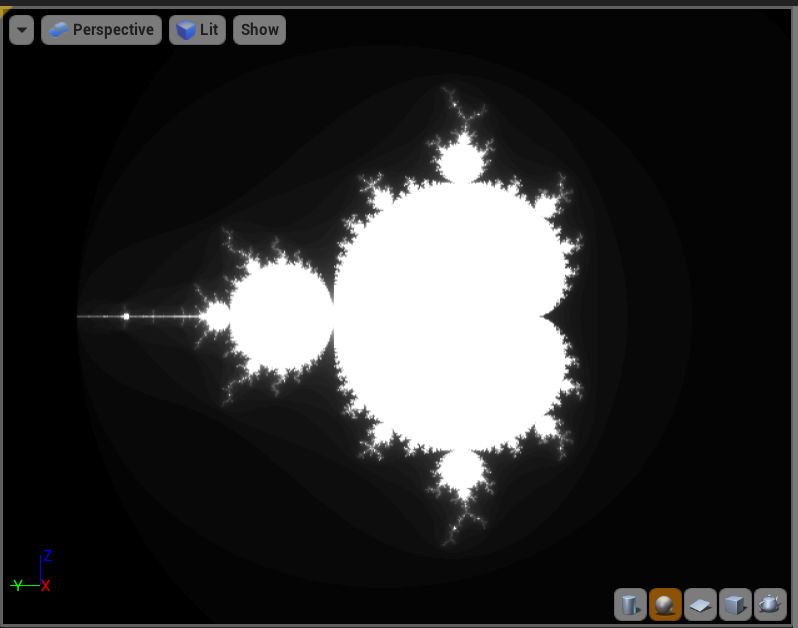
然后我们就可以得到以下的结果：

三、朱利亚集合实现

根据上面的过程我们知道了曼德勃罗集合的实现方式，而朱利亚集合和曼德勃罗集合只有一 C之差，为什么这么说呢，看完做法你就知道了。

从上篇文章 中我们知道朱利亚集合是将位置代入 Z中，然后改变定值 C实现的，于是我们还是套用上面曼德勃罗集合的节点，只不过因为这里我们将 C定义为定值，所以还需要再多设置一个位置的变量将平面上的二维坐标(也就是uv)传入。

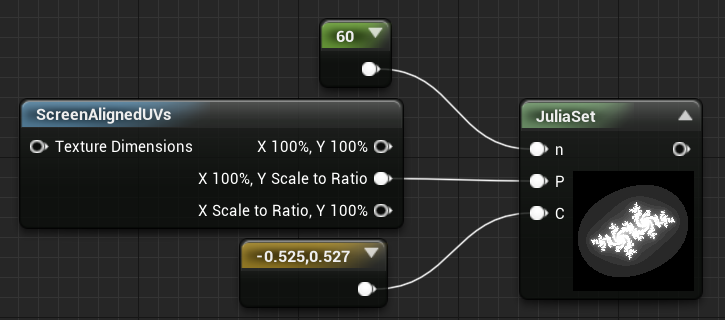
和上面很类似是不是，但是这里我将 C变成了一个定值，而P则作为复平面上点坐标传入的变量。于是我们的代码也需要做一点小调整，不是很大。改动的地方我已经用红色字体标出了(虽然代码红色部分确实不一样了，但是你需要明确知道的是，朱利亚集合图像和曼德勃罗集合图像不同的原因在于 C的变化，想要温习请看上一章：分形的基础讲解)：

// 将屏幕uv空间缩放至原来的两倍并将0点挪到屏幕中心

P = P * 4 - 2;

// 统一定义一些必要的变量

floatx = P.x, y = P.y, xnew, ynew;

// 复变函数循环开始

for (inti = 0; i

{

// 将上面推导出来的公式运用进去

xnew = x*x - y*y + C.x;

ynew = 2*x*y + C.y;

// 判断迭代后复数的长度是否大于2，如果大于就返回他逃离所用的次数与总次数的比值(这里大于4是因为没有算平方根)

if( xnew*xnew + ynew*ynew > 4 ){

return (float)i / (float)n;

}

// 将函数的结果值赋予函数本身迭代计算

x=xnew;

y=ynew;

}

// 循环完成返回最大次数值(其实可以是1)

return(n);

接下来我们应用代码，修改 C的值就可以看到如下结果：

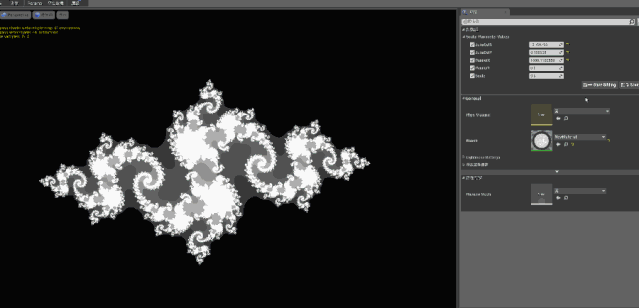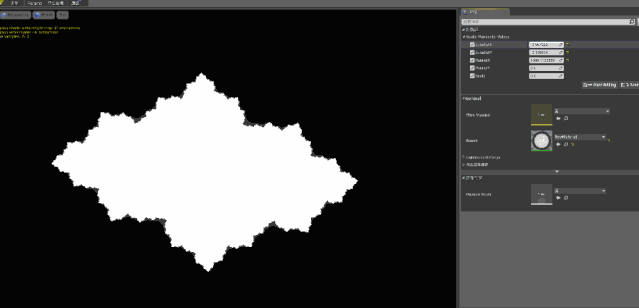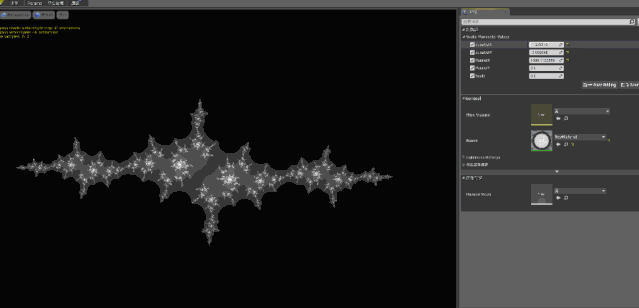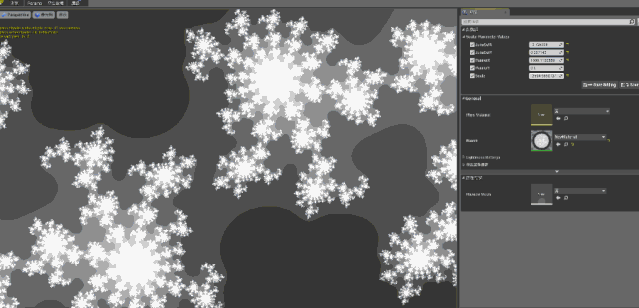
好的既然分形都画出来了，那本文到这里就结束了吗？

并 没 有！

还记得我们上期说的Z = Z^n + C吗？既然在 n = 2时我们可以化简成上面的形式，那如果 n不固定呢，我们要怎么去做这个化简操作？

其实是可以化简的！但是可能会比上面化简的操作更加复杂，接下来请各位读者跟着我一起看下去，看看这个带 n次方的复变函数如何推导成 Z = a + bi的形式！

四、Z = Z^n + C 函数分解与实现

首先我们还是定义:

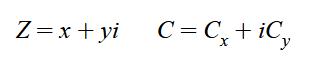
然后替换原始复变函数得：

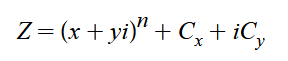
下面我放一张复平面的图片，复平面你可以理解成就是复数的平面直角坐标系，大家可以对着这张图往下看：

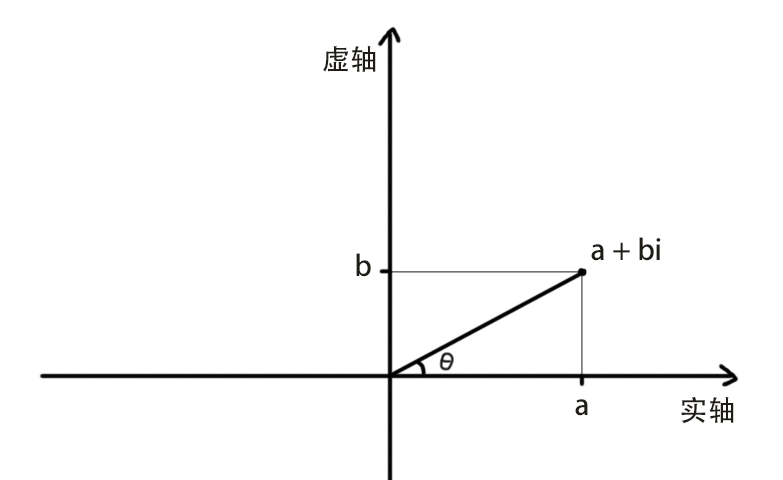
这里我们将x + yi写成如下形式：

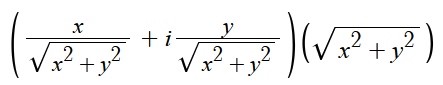
如果我们定义复数与实数轴正方向的夹角为 θ，那么根据三角函数的基础计算原理可以得到：

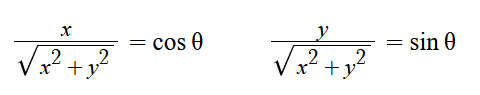
于是我们代入公式：

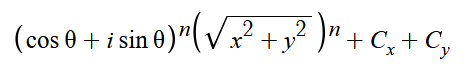
看到这里，cosθ+isinθ，是不是联想到了什么？？对！就是大名鼎鼎的欧拉公式！

接下来我们将其替换，可以得到：

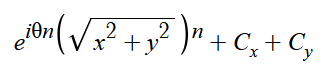
有意思的地方来了，如果我们将θn看成一个整体，再反向运用一次欧拉公式，就可以得到：

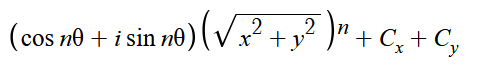
哇这样 n次方就没有了，感谢欧拉！！！！

这时我们就已经将实部虚部分开了，得到了下面两个公式：

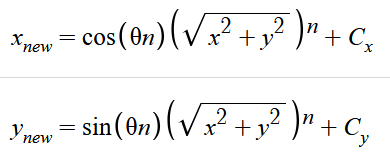
这里我们用反三角函数推导出 θ=atan(y.x)，而根号 x²+y²其实就是复数的长度，将结果代入计算得：

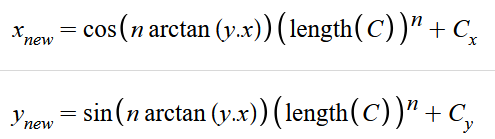
这！就是我们最终需要写入代码的公式 ！！！

数学真奇妙 ！！！！！

剩下的实现步骤就很简单了，和上面一样，我们只需要将复变函数替换成我们刚刚算出来的这一套即可，节点设置如下。这里我将迭代次数设置成 times，指数设置成 n，C依然还是那个 C。

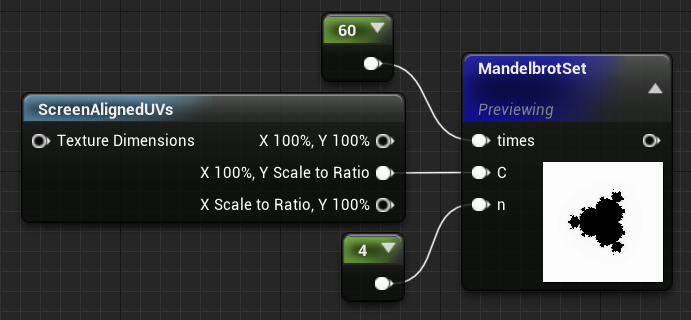
代码时间到，其实具体内容和上面 n=2时差距并不是很大，只是修改了复变函数部分的算法：

// 统一定义一些必要的变量

floatxnew , ynew ;

float2znew, z = (0,0);

// 将屏幕uv空间缩放至原来的两倍并将0点挪到屏幕中心

C = C * 4 - 2;

// 复变函数循环开始

for (inti = 0; i

{

// 将上面推导出来的公式运用进去，这里整合成float2是为了方便算长度

znew = float2(

cos( atan(z.y/z.x)*n)*pow(length(z),n),

sin ( atan(z.y/z.x)*n)*pow(length(z),n)

)+C;

// 判断迭代后复数的长度是否大于2，如果大于就返回他逃离所用的次数与总次数的比值(这里大于4是因为没有算平方根)

if(length(znew)>4){

return (float)i/(float)times;

}

// 将函数的结果值赋予函数本身迭代计算

z.x=znew.x;

z.y=znew.y;

}

// 循环完成返回最大次数值(其实可以是1)

return(times);

于是我们可以通过改变 n值使曼德勃罗集合愉快的变化起来了！！

看完本文的推导和实现，相信你已深深感受到数学的美妙，没错数学就是这样一门迷人的学科！其实在这里我还留了一个 n次方时朱利亚集合的效果没有做，如果你对此感兴趣，可以自己尝试着实现一下~

最后感谢展新大佬在我研究分形时提供的大量支持，没有他的指导我是不可能写出这篇文章的！

如果你喜欢这篇文章的话，记得点在看转发收藏哟 ~ 么么扎！返回搜狐，查看更多

责任编辑：