香雪海教育
有理数乘法法则及相关运算律的知识学了之后,常遇到负带分数与整数相乘的题型。基础薄弱的很多学生理解不了负带分数的整数部分与分数部分的关系,常常导致计算出错。怎么帮助学生走出误区?笔者以为归类讲析不失为一个好办法。
下面以人教社《人教金学典——同步解析与测评》(七上)所选题目为例,进行归类讲析,冀望更多学生受益。
题目一:

这里的例2第(2)小题就是负带分数与整数相乘的题型。这里明确提示了简便算法:先把--99又5/6拆成--100+1/6,再运用分配律计算。但是才学了负数的加、减、乘法的学生还反应不过来,看不懂拆数这一步(尖子生除外)。我们可以先类比:99又5/6=99+5/6,那么--99又5/6=--99+(--5/6),而不是--99+5/6。再用法则检验:能还原的就正确,否则就是错误的。有理数加法法则:同号两数相加,取相同的符号,并把绝对值相加;绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。因此,运用前一条法则,--99+(--5/6)=--[∣--99∣+∣--5/6∣]=--[99+5/6]=--99又5/6,能还原,表明拆数是正确的。运用后一条法则,--99+5/6=--[∣--99∣--∣5/6∣]=--[99--5/6]=--98又1/6≠--99又5/6,不能还原,表明拆数是错误的。为了计算简便,可以凑整,于是--99又5/6=--99+(--5/6)=(--99--1)+[1+(--5/6)]=--100+1/6。接下来利用分配律的过程就好理解了。
题目二:

解:(1)两种解法比较,小莉的比较简便,因为利用乘法分配律使运算量变小了。小强在把带分数与假分数互化时,因数字较大,不利于口算,不简便。
(2)原式=(70+31/16)×(--8)=70×(--8)+31/16×(--8)=--560--31/2=--575又1/2
或原式=--[(71+1)+15/16--1]×8=--[72×8--1/16×8]=--[576--1/2]=--575又1/2
(3)原式=(--99--98/99--1+1)×198=(-100+1/99)×198=--100×198+1/99×198=--19798
题目三:

只要理解了--3又3/4=--3+(--3/4)=--3--3/4,就知道选A项。
题目四:

解:(1)原式=(--100--35/6)×12=--1200--70=--1270
题目五:
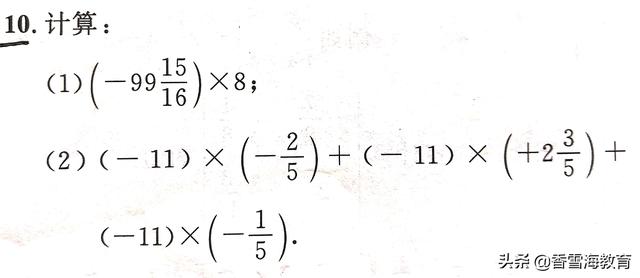
解:(1)原式=(--100+1/16)×8=--800+1/2=--799.5
题目六:

解:(3)原式=--(10--1/19)×19=--(190--1)=--189
总之,只要理解了负带分数是负整数与负分数的和,上面这类问题的解决就不容易出错了。







 学习有理数乘法法则及运算律后,负带分数与整数相乘题型常让基础薄弱学生出错。本文以人教社相关题目为例,通过类比、法则检验等方法,对该题型进行归类讲析,帮助学生理解负带分数是负整数与负分数的和,从而正确解题。
学习有理数乘法法则及运算律后,负带分数与整数相乘题型常让基础薄弱学生出错。本文以人教社相关题目为例,通过类比、法则检验等方法,对该题型进行归类讲析,帮助学生理解负带分数是负整数与负分数的和,从而正确解题。
















 728
728

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








