简介:数独是一款基于逻辑的数字填充游戏,要求在9x9格子中填入数字,满足每行、每列及九个3x3宫格内数字1至9不重复。Sudoku-game项目旨在创建一个完整的数独游戏系统,包括生成器和求解器。生成器负责创建具有唯一解的数独谜题,而求解器则找出给定初始条件下所有可能的解决方案。该项目使用C++编程语言,涉及到多种算法设计、数据结构、用户界面设计、性能优化和测试调试。此外,项目还可能包含源代码管理和持续集成/持续部署(CI/CD)的实践。 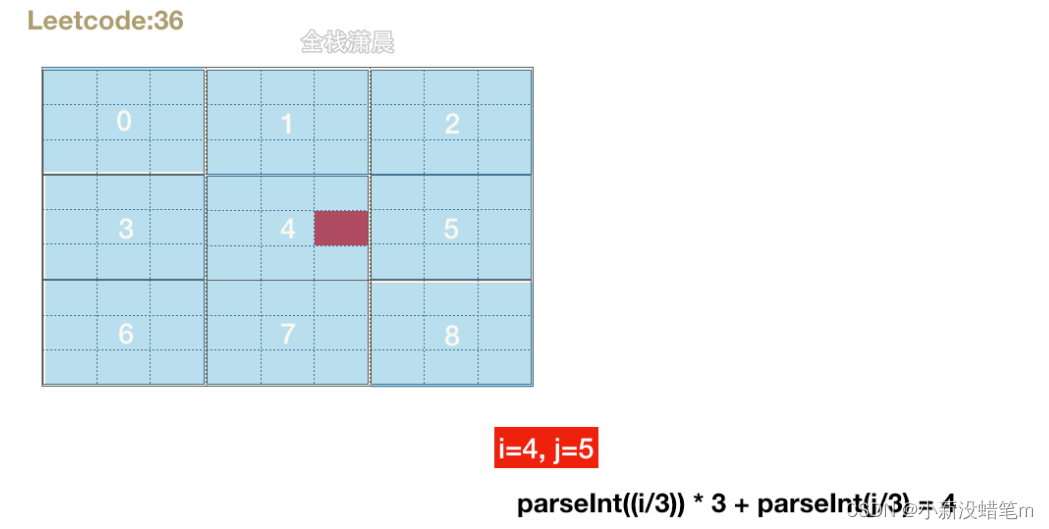
1. 数独游戏逻辑和规则
数独是一种经典的逻辑填数字游戏,它由9个3x3的小格子组成一个大格子,游戏的规则是在这个9x9的矩阵中填入1至9的数字,每个数字在每一行、每一列以及每个小格子中只能出现一次。这一章节将详细介绍数独游戏的基本规则,以及它所蕴含的数学逻辑和解题技巧。
1.1 游戏规则概述
数独的规则非常简单:在9x9的网格中,根据已有的数字提示,填写1至9的数字,使得每一行、每一列以及每一个3x3的小格子中的数字都不重复。解题时,需要运用逻辑推理来逐步缩小可能数字的范围,直至找到唯一解。
1.2 数独的魅力与益智性
数独游戏不仅趣味性强,还具有很高的益智性。它能够锻炼玩家的逻辑思维能力、空间想象力和记忆力。数独游戏适合所有年龄段的人群,对于提升大脑的敏捷性和集中力有着明显的效果。
1.3 数独游戏的变种
随着数独游戏的普及,出现了许多变种和升级版数独,例如异形数独、杀手数独、连数数独等。这些变种在规则上有所创新,增加了游戏的难度和趣味性,为数独爱好者提供了更多选择。在本章的后续内容中,我们将对各种数独的玩法进行详细介绍和分析。
数独游戏的这些变种规则将在后续章节中根据算法的实现,结合具体编程语言进行逻辑推理的实现和分析。随着我们逐步深入,读者将能够了解到如何通过编程实现这些复杂且富有趣味性的数独规则。
2. 数独生成器的设计实现
设计一个优秀的数独生成器,是数独游戏开发中最为关键的部分之一。一个好的生成器不仅能生成符合规则的谜题,还应该具备良好的可扩展性和灵活性,能够生成不同难度级别的数独。本章将深入探讨数独生成器的基本与高级算法,包括它们的设计思路和实现细节。
2.1 基本生成算法
2.1.1 随机填数法
随机填数法是最为基础的一种生成算法,它简单、直观,通常适用于生成初学者级别的数独谜题。实现的基本思路是随机选择空白单元格,然后随机选择一个不违反数独规则的数字填充。
#include <iostream>
#include <vector>
#include <algorithm>
#include <ctime>
// A utility function to print the board
void printBoard(std::vector<std::vector<int>>& board) {
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
std::cout << board[i][j] << " ";
}
std::cout << std::endl;
}
}
// Randomly fills the empty cells of a given Sudoku board
bool fillRandomly(std::vector<std::vector<int>>& board, int& emptyCells) {
int row, col;
int num = 1;
bool valid;
// Seed the random number generator
srand(time(NULL));
while (emptyCells > 0) {
row = rand() % 9;
col = rand() % 9;
// Skip if cell is already filled
if (board[row][col] != 0) continue;
// Check for a valid number
for (int k = 0; k < 9; k++) {
if (board[row][k] == num || board[k][col] == num) {
valid = false;
break;
}
int boxRow = (row / 3) * 3 + k / 3;
int boxCol = (col / 3) * 3 + k % 3;
if (board[boxRow][boxCol] == num) {
valid = false;
break;
}
}
// Fill the cell if the number is valid
if (valid) {
board[row][col] = num;
emptyCells--;
}
// Increment the number if nothing is found
if (!valid) num++;
}
// Check if the board is completely filled
return num <= 9;
}
在上述代码中,我们尝试随机填充空单元格,同时确保数字不违反数独的规则。如果发现所选数字不合法,我们就增加数字并重新尝试。这可以通过在 fillRandomly 函数中循环执行来完成。值得注意的是,这种方法可能不会生成一个唯一解的数独谜题,也不会考虑不同难度级别的生成。
2.1.2 基于数独规则的生成策略
为了生成一个满足唯一解要求的数独谜题,并且可以控制谜题的难度,基于数独规则的生成策略则更为复杂和精细。一个常见的方法是首先生成一个合法的数独解,然后通过系统地消除一定数量的数字来创建一个谜题。这种方法的关键在于如何平衡剩余数字的数量以控制难度。
// A utility function to check if a number can be placed in the cell
bool isValid(std::vector<std::vector<int>>& board, int row, int col, int num) {
for (int d = 0; d < board.size(); d++) {
if (board[row][d] == num || board[d][col] == num) {
return false;
}
if (board[3 * (row / 3) + d / 3][3 * (col / 3) + d % 3] == num) {
return false;
}
}
return true;
}
// A recursive function to fill the board
bool solveSudoku(std::vector<std::vector<int>>& board) {
int row = -1;
int col = -1;
bool isEmpty = true;
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
if (board[i][j] == 0) {
row = i;
col = j;
isEmpty = false;
break;
}
}
if (!isEmpty) {
break;
}
}
if (isEmpty) {
return true; // board is filled
}
for (int num = 1; num <= board.size(); num++) {
if (isValid(board, row, col, num)) {
board[row][col] = num;
if (solveSudoku(board)) {
return true;
}
board[row][col] = 0; // reset the cell for backtracking
}
}
return false; // triggers backtracking
}
// Function to remove numbers from the solved board to make a puzzle
void createSudokuPuzzle(std::vector<std::vector<int>>& board, int emptyCellsToLeave) {
// Solve the board to get a valid solution
solveSudoku(board);
int emptyCells = board.size() * board[0].size() - emptyCellsToLeave;
int i = 0, j = 0;
while (emptyCells > 0) {
do {
j++;
if (j > board.size() - 1) {
j = 0;
i++;
}
if (i > board.size() - 1) {
break;
}
} while (board[i][j] != 0);
if (i > board.size() - 1) {
break;
}
board[i][j] = 0;
emptyCells--;
// Check if the puzzle is still valid
if (!solveSudoku(board)) {
board[i][j] = 0; // Put the number back if puzzle is invalid
emptyCells++;
}
}
}
在这段代码中,首先使用 solveSudoku 函数解决一个完全空的数独板,然后通过 createSudokuPuzzle 函数来移除一定数量的单元格中的数字,以生成一个有难度的谜题。需要注意的是,这个过程中需要确保剩余的数字数量仍然能够保证谜题具有唯一解。
2.2 高级生成算法
2.2.1 启发式算法的探讨
尽管基于规则的策略能够生成具有挑战性的数独谜题,但这种方法可能会消耗较多的时间和资源,尤其是在追求高效生成时。启发式算法在数独生成中提供了一个更加高效的选择。启发式算法通常通过预定义规则和启发式评估函数来指导搜索过程,以快速定位到有效解决方案。
2.2.2 算法性能比较与优化
本节将比较几种常见的启发式算法(例如模拟退火、遗传算法等)在数独生成中的性能,探讨如何通过算法优化提高生成效率。为了优化算法性能,需要对算法的各个阶段进行细致的分析,例如设置合理的温度下降计划、选择合适的交叉和变异策略等。
graph LR
A[开始] --> B[生成初始种群]
B --> C[评估种群]
C --> D[选择操作]
D --> E[交叉操作]
E --> F[变异操作]
F --> G{是否满足条件?}
G --> |是| H[输出结果]
G --> |否| C
在上述的mermaid流程图中,我们简要展示了遗传算法的基本流程。首先生成一个随机种群,然后进行种群评估,接着是选择、交叉和变异操作,最终判断是否满足结束条件。通过不断重复这个过程,直至找到满意的解决方案为止。
请继续阅读下一章节,以获取关于数独求解器设计实现的详细信息。
3. 数独求解器的设计实现
3.1 算法设计基础
3.1.1 回溯法原理与实现
回溯法是一种通过递归的方式,对所有可能的解空间进行遍历的算法。在数独求解中,回溯法的基本思想是从空白位置开始,逐个尝试填入数字1-9,并且每填一个数字就检查当前的棋盘状态是否符合数独的规则。如果当前填入的数字导致后续无法继续,则回溯到上一个状态,尝试另一个数字。
bool solveSudoku(vector<vector<char>>& board) {
for (int i = 0; i < board.size(); ++i) {
for (int j = 0; j < board[0].size(); ++j) {
if (board[i][j] == '.') {
for (char c = '1'; c <= '9'; ++c) {
if (isValid(board, i, j, c)) {
board[i][j] = c;
if (solveSudoku(board)) {
return true;
}
board[i][j] = '.';
}
}
return false;
}
}
}
return true;
}
3.1.2 遗传算法原理与实现
遗传算法是一种模拟自然界生物进化过程的搜索算法,通过迭代的方式,从一组候选解开始,利用选择、交叉和变异操作产生新的候选解。在数独求解中,遗传算法首先生成一组随机解,然后通过交叉和变异操作产生新个体,并不断迭代直到找到一个合法的解。
void initPopulation(vector<vector<char>>& population) {
// 初始化种群,随机生成数独解
}
void select(vector<vector<char>>& population) {
// 选择操作,根据适应度选择优秀个体
}
void crossover(vector<vector<char>>& parent1, vector<vector<char>>& parent2, vector<vector<char>>& child1, vector<vector<char>>& child2) {
// 交叉操作,产生新个体
}
void mutate(vector<vector<char>>& individual) {
// 变异操作,随机改变个体中的某些基因
}
bool遗传算法解数独(vector<vector<char>>& board) {
vector<vector<char>> population;
initPopulation(population);
while (/*未达到结束条件*/){
select(population);
crossover(population);
mutate(population);
if (solveSudoku(board)) {
return true;
}
}
return false;
}
3.2 算法优化策略
3.2.1 CSP算法在数独求解中的应用
约束满足问题(Constraint Satisfaction Problem, CSP)是人工智能领域的一个重要问题类型。数独可以看作是一个CSP问题,其中的变量是每个空格,每个变量的域是1-9,约束条件是每一行、每一列和每一个3x3宫内的数字必须唯一。通过将数独视为CSP问题,可以使用通用的CSP解法,例如前向检查、最小剩余值(MRV)启发式、度数优先(Degree)启发式等。
3.2.2 求解过程中的剪枝技术
剪枝技术是优化搜索过程中的关键环节,旨在减少不必要的搜索空间,从而提高算法效率。在数独求解中,可以利用以下几种剪枝技术:
- 前向检查 :每填一个数字,就检查它所在的行、列和宫内是否有其他位置不能再填入该数字,如果有,则剪掉这些位置作为候选解。
bool forwardCheck(vector<vector<char>>& board) {
// 实现前向检查逻辑,剪枝不必要的候选解
}
-
MRV启发式 :优先选择剩余可填数字最少的空格进行填充,因为这样的位置更容易产生剪枝效果。
-
度数优先 :优先选择与已填数字冲突最多的空格进行填充,以此来减少搜索空间。
通过结合这些剪枝技术,算法在求解过程中可以大幅度减少需要考虑的解空间大小,从而提高求解速度和效率。
4. C++编程语言在数独游戏中的应用
4.1 C++基础语法及面向对象编程
4.1.1 C++基础语法回顾
C++是一种静态类型、编译式、通用的编程语言,它支持过程化编程、面向对象编程以及泛型编程。作为数独游戏开发中的基础语言,掌握C++的语法对于实现游戏逻辑至关重要。本节将回顾一些C++的基础语法,如变量定义、控制结构、函数、以及类的基本概念。
首先,变量的定义和初始化是编程中最基本的操作。在C++中,我们可以使用 int 、 float 、 bool 等关键字来声明变量。例如:
int a = 10; // 整型变量
float b = 3.14f; // 浮点型变量
bool flag = true; // 布尔型变量
接着,控制结构是编写复杂逻辑的基石,C++提供了诸如 if-else 、 for 、 while 、 do-while 等控制结构。例如,使用 for 循环来遍历数组:
int array[5] = {1, 2, 3, 4, 5};
for(int i = 0; i < 5; ++i) {
// 访问数组中的元素
std::cout << array[i] << std::endl;
}
函数是C++中组织代码的另一个关键要素。一个函数拥有返回类型、函数名、参数列表和函数体。这里是一个简单的函数定义示例:
int add(int x, int y) {
return x + y;
}
最后,面向对象编程的核心在于类的定义。类是创建对象的蓝图,其中封装了数据和操作这些数据的方法。以下是一个简单的类定义和使用示例:
class SudokuCell {
public:
SudokuCell() : value(0) {} // 构造函数
void setValue(int val) { value = val; }
int getValue() const { return value; }
private:
int value;
};
int main() {
SudokuCell cell;
cell.setValue(5);
std::cout << cell.getValue() << std::endl; // 输出:5
return 0;
}
理解C++的基础语法是实现数独游戏逻辑的前提。开发者需要熟练地使用这些语法特性来组织代码并解决编程问题。
4.1.2 面向对象编程核心概念
面向对象编程(OOP)是一种编程范式,它围绕着对象的概念组织软件设计和开发过程。在C++中,OOP的核心概念包括类与对象、继承、多态以及封装。这些概念在数独游戏的设计与实现中起到了至关重要的作用。
类与对象
类是创建对象的模板,对象是类的实例。类可以包含数据成员(变量)和成员函数(方法),成员函数可以操作对象的状态。例如:
class Sudoku {
public:
void solve() { /* 解数独的逻辑 */ }
void display() const { /* 显示数独的逻辑 */ }
private:
int grid[9][9]; // 数独盘面的9x9网格
};
在上面的类定义中, Sudoku 对象拥有解决数独游戏的方法 solve() 和显示当前游戏状态的方法 display() 。
继承
继承是OOP中的一种机制,它允许创建一个类(子类)继承另一个类(父类)的属性和方法。这在设计数独游戏时,可以用来表示不同级别的难度或特定的数独变种。例如:
class ClassicSudoku : public Sudoku {
public:
void generateClassicPuzzle() { /* 生成经典数独谜题的逻辑 */ }
};
class SamuraiSudoku : public Sudoku {
public:
void generateSamuraiPuzzle() { /* 生成五宫数独谜题的逻辑 */ }
};
这里, ClassicSudoku 和 SamuraiSudoku 类分别继承了 Sudoku 类,并且添加了特定的方法来生成不同类型的数独谜题。
多态
多态指的是同一个接口可以使用不同的实例而执行不同的操作。在C++中,多态通过虚函数实现。多态允许开发者编写更加灵活和可扩展的代码。例如:
class AbstractSudokuSolver {
public:
virtual void solve(Sudoku& board) = 0; // 纯虚函数定义
};
class BacktrackingSolver : public AbstractSudokuSolver {
public:
void solve(Sudoku& board) override { /* 回溯算法求解 */ }
};
class GeneticSolver : public AbstractSudokuSolver {
public:
void solve(Sudoku& board) override { /* 遗传算法求解 */ }
};
在这里, AbstractSudokuSolver 类定义了一个纯虚函数 solve() 。 BacktrackingSolver 和 GeneticSolver 两个派生类通过重写这个函数提供不同的求解策略。
封装
封装是将数据(或状态)和操作数据的代码捆绑在一起的过程,这有助于隐藏对象的内部实现细节,保护对象内部状态不被外部访问和修改。在C++中,通过访问修饰符(如 public 、 private 和 protected )来实现封装。例如:
class SudokuCell {
private:
int value; // 私有成员变量,封装了Sudoku单元格的值
public:
explicit SudokuCell(int val) : value(val) {} // 构造函数
int getValue() const { return value; } // 公有成员函数,提供获取值的接口
void setValue(int val) { value = val; } // 公有成员函数,提供设置值的接口
};
在 SudokuCell 类中, value 是一个私有成员变量,它只能通过公有成员函数 getValue() 和 setValue() 来访问和修改。这样,封装确保了对象的状态不会被外部代码错误地修改。
掌握面向对象编程的核心概念是利用C++进行复杂程序设计的关键。在数独游戏开发过程中,合理运用这些概念可以使得代码更加模块化、易于理解和维护。
4.2 C++高级特性应用
4.2.1 智能指针与资源管理
C++语言提供了多种内存管理技术,但手动管理内存容易出错,特别是忘记释放资源会导致内存泄漏。为了解决这一问题,C++11引入了智能指针,这是一种资源获取即初始化(RAII)的实践方式,能够自动管理内存生命周期。智能指针包括 std::unique_ptr 、 std::shared_ptr 和 std::weak_ptr 。
std::unique_ptr
std::unique_ptr 是一种独占所有权的智能指针,当 std::unique_ptr 离开作用域时,它所指向的对象会被自动删除。 std::unique_ptr 不能被复制,但可以被移动。例如:
#include <memory>
void foo() {
std::unique_ptr<int> ptr(new int(10)); // 创建一个unique_ptr对象
// 使用ptr,例如访问其成员,使用其操作符等
} // ptr离开作用域,所指向的内存被自动释放
int main() {
foo(); // 调用函数,管理其自己的内存
return 0;
}
在这个例子中, foo 函数使用 std::unique_ptr 管理一个动态分配的整数对象。当 foo 函数结束时, ptr 离开作用域,动态分配的内存被自动释放。
std::shared_ptr
当需要多个指针共享同一个资源时,可以使用 std::shared_ptr 。它的内部实现使用引用计数机制跟踪有多少个 shared_ptr 实例指向同一个对象。当最后一个 shared_ptr 被销毁或重新赋值时,对象将被自动删除。例如:
#include <memory>
int main() {
std::shared_ptr<int> ptr1(new int(10));
std::shared_ptr<int> ptr2 = ptr1; // ptr2共享ptr1指向的对象
// 两个shared_ptr共享同一个对象
// 只有当ptr1和ptr2都被销毁时,对象才会被删除
return 0;
}
在这个例子中, ptr1 和 ptr2 共享一个动态分配的整数对象。它们的引用计数会相应地增加和减少,确保对象在不再需要时被正确删除。
std::weak_ptr
std::weak_ptr 是一个不控制资源生命周期的智能指针。它可以指向一个由 std::shared_ptr 管理的对象,但不会增加引用计数。这常用于打破 shared_ptr 的循环引用,防止内存泄漏。例如:
#include <memory>
int main() {
std::shared_ptr<int> shared = std::make_shared<int>(10);
std::weak_ptr<int> weak(shared); // 创建一个weak_ptr指向shared
// shared被销毁时,weak的引用不会阻止资源被释放
return 0;
}
在这个例子中, weak 创建了一个指向 shared 管理的对象的弱引用。如果 shared 是唯一一个 shared_ptr ,当 main 函数结束时, shared 指向的资源会被释放,即使 weak 仍然存在。
智能指针是现代C++编程中管理资源的首选方法,它们提供了更加安全和方便的方式来管理动态内存,从而减少了内存泄漏和其他内存相关错误的风险。在数独游戏的开发过程中,合理利用智能指针不仅可以优化内存管理,还能提高代码的健壮性。
4.2.2 C++11及以上版本的新特性应用
随着C++11及之后版本的发布,C++语言引入了大量新的特性和改进。这些特性不仅使得C++更加现代化,还大大提高了编程的效率和安全。在数独游戏的开发中,可以利用C++11及以上版本的新特性来实现更优的性能和代码质量。
初始化列表
C++11引入了初始化列表的概念,允许开发者用更简洁、更直观的方式来初始化对象。在创建数组、容器等时特别有用。例如:
std::vector<int> v = {1, 2, 3, 4, 5};
std::map<std::string, int> m = {{"one", 1}, {"two", 2}, {"three", 3}};
移动语义
传统的C++中,拷贝构造函数和赋值操作符用于复制对象。但复制大对象时可能代价昂贵。C++11提供了移动语义,允许开发者将资源从一个对象转移到另一个对象,从而提高效率。例如:
std::vector<std::unique_ptr<int>> v1;
for (int i = 0; i < 100; ++i) {
v1.emplace_back(new int(i));
}
std::vector<std::unique_ptr<int>> v2 = std::move(v1);
// v1中的资源现在被转移到了v2中,v1变为空容器
Lambda表达式
Lambda表达式允许开发者定义匿名函数对象,这在需要函数作为参数的场合非常有用,如标准库算法、事件处理等。例如:
std::vector<int> nums = {1, 2, 3, 4, 5, 6, 7, 8, 9};
std::for_each(nums.begin(), nums.end(), [](int& num) {
num *= 2;
});
// 使用lambda表达式将所有数字乘以2
基于范围的for循环
C++11中的基于范围的for循环简化了数组和容器遍历的过程。例如:
std::vector<int> nums = {1, 2, 3, 4, 5};
for (int num : nums) {
std::cout << num << std::endl;
}
// 输出nums中的所有元素
可变参数模板
可变参数模板允许创建函数或类来接受任意数量和类型的参数,这在实现通用库或灵活的函数时非常有用。例如:
template <typename... Args>
void print(const Args&... args) {
(std::cout << ... << args) << std::endl;
}
print(1, "two", 3.0, "four"); // 输出:1 two 3 four
这些新特性提供了更简洁的语法、更高效的资源管理、以及更强大的编程能力。在开发数独游戏时,合理地利用这些新特性可以使代码更加优雅、性能更加高效。
合理运用C++11及以上版本的新特性可以显著提升开发效率和程序性能。在数独游戏的开发过程中,采用这些现代C++编程实践有助于创建出更加健壮和易于维护的代码。
5. 数独游戏的算法与数据结构
5.1 关键数据结构设计
5.1.1 二维数组的使用与优化
二维数组是实现数独游戏最为直观和基础的数据结构。在C++中,二维数组可以方便地模拟数独游戏的九宫格布局,并且可以很容易地访问和修改每一个格子。为了优化二维数组在数独游戏中的使用,我们需要考虑以下几个方面:
- 内存分配 :通常情况下,二维数组在栈上分配,对于大数组而言,这可能会导致栈溢出。因此,我们可以考虑使用动态分配,在堆上创建一个指针数组,这样可以更好地控制内存使用并避免栈溢出。
-
边界检查 :在对二维数组进行操作时,需要进行有效的边界检查。例如,在访问
board[row][col]时,需要确认row和col是否在有效范围内,即0 <= row < 9且0 <= col < 9。 -
访问效率 :为了提高访问效率,尤其是在频繁访问数组元素的情况下,我们可以采用连续存储的方式来访问二维数组。在C++中,连续内存块的访问速度比非连续内存块要快。
-
功能扩展 :二维数组本身功能较为单一,因此我们可以考虑将二维数组封装成类,在类中实现更多高级功能,比如验证行、列和子宫格的完整性和有效性。
下面是一个在堆上动态分配二维数组的示例代码:
#include <iostream>
int main() {
int **board = new int*[9];
for (int i = 0; i < 9; ++i) {
board[i] = new int[9];
}
// 填充数据
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
board[i][j] = 0; // 初始化为0或其他默认值
}
}
// 使用board
// 释放内存
for (int i = 0; i < 9; ++i) {
delete[] board[i];
}
delete[] board;
return 0;
}
5.1.2 自定义类的设计与实现
在数独游戏的设计中,单纯使用二维数组可能会导致代码可读性差、难以维护等问题。为了提高代码的可维护性和可扩展性,我们可以设计一个或多个类来封装二维数组以及数独的其他相关操作。
- 类的功能 :类中可以包含初始化、显示数独游戏板、设置和清除格子、检查行/列/宫格的有效性等方法。
-
数据封装 :通过私有成员变量来存储二维数组,公共接口提供操作这些数据的方法。
-
代码示例 :下面展示了如何设计一个简单的
Sudoku类:
#include <iostream>
#include <vector>
class Sudoku {
private:
std::vector<std::vector<int>> board;
public:
Sudoku() : board(9, std::vector<int>(9, 0)) {}
void display() const {
for (const auto &row : board) {
for (int num : row) {
std::cout << num << " ";
}
std::cout << std::endl;
}
}
void setNumber(int row, int col, int num) {
if (row >= 0 && row < 9 && col >= 0 && col < 9) {
board[row][col] = num;
}
}
bool isValidNumber(int row, int col, int num) const {
// 验证num是否可以放置在[row, col]位置的逻辑
return true; // 示例中简化了验证逻辑
}
};
int main() {
Sudoku sudoku;
sudoku.display(); // 显示初始空板
// 进行数独游戏的一些操作,如设置数字等
return 0;
}
在这个例子中,我们用 std::vector 替代了原始的指针数组,利用C++标准库提供的动态数组功能,简化了内存分配和释放的代码,提高了代码的安全性和可读性。
5.2 算法在数独游戏中的应用
5.2.1 算法设计与实现过程
在数独游戏的算法实现中,首要的是设计能够生成数独游戏棋盘的算法以及能够求解数独谜题的算法。算法的设计和实现过程通常包括以下几个步骤:
-
需求分析 :确定算法需要解决的问题是什么,比如生成一个具有唯一解的数独棋盘。
-
算法设计 :选择合适的算法框架来实现功能,例如生成器可以使用回溯算法,求解器可以使用回溯法或回溯算法的变种如深度优先搜索。
-
伪代码编写 :将算法的思路转化成伪代码,有助于理解算法的结构和流程。
-
编码实现 :将伪代码转化为具体的编程语言代码。
-
测试与调试 :验证算法的正确性,并对可能存在的问题进行调试。
-
性能分析 :评估算法的时间和空间复杂度,并进行必要的优化。
下面是一个简单的回溯算法伪代码,用于解决数独问题:
function solveSudoku(board):
if board is solved:
return true
for each cell in board:
if cell is empty:
for each possible number in cell:
if isNumberValid(board, cell, number):
place number in cell
if solveSudoku(board):
return true
remove number from cell
return false
5.2.2 算法性能分析与优化
算法性能的分析和优化是整个数独游戏设计中至关重要的一个环节。我们需要关注的性能指标通常有时间复杂度和空间复杂度。
-
时间复杂度 :涉及算法运行时间随输入规模的增加而增长的速度。例如,回溯算法的时间复杂度通常是指数级的,但通过优化剪枝策略可以有效减少搜索空间,提高效率。
-
空间复杂度 :涉及算法运行时所占用的内存空间。通过动态内存分配和数据结构优化,可以降低空间复杂度。
-
优化方法 :剪枝是数独算法中常用的优化方法之一,通过在搜索过程中判断某些路径不可能导致问题的解决而提前结束搜索。
-
性能测试 :通过不同的测试用例来验证算法的性能,如随机生成的数独棋盘、特定难度等级的棋盘等。
以回溯算法为例,优化后的伪代码如下:
function solveSudokuOptimized(board):
if board is solved:
return true
for each cell in board:
if cell is empty:
for each possible number in cell:
if isNumberValid(board, cell, number):
place number in cell
if solveSudokuOptimized(board):
return true
remove number from cell
if all numbers have been tried and none worked:
break
return false
在上述伪代码中,新增了一个判断条件,如果所有可能的数字都不能解决数独问题,则立即退出循环,这有助于减少不必要的计算。此外, isNumberValid 函数可以进一步优化,例如通过检查数独的行、列和宫格规则来提前判断某个数字是否可能是一个解。
通过本章节的介绍,我们了解到如何在数独游戏中设计和实现关键的数据结构,并在实际应用中不断优化算法性能,以达到更佳的游戏体验。
6. 数独游戏的用户界面与性能优化
用户界面是软件应用的门面,良好的用户体验往往可以提升产品的价值。对于数独游戏而言,用户界面的设计尤为关键,因为它直接影响到玩家的互动体验。性能优化则是为了确保数独游戏在运行时可以流畅无阻,响应迅速。持续集成/部署(CI/CD)是现代软件开发中的重要实践,它能确保代码的持续集成和高效部署。接下来,我们将详细探讨用户界面设计、性能优化的策略以及源代码管理与CI/CD流程。
6.1 用户界面设计
数独游戏的用户界面设计可以分为两大类:文本界面和图形界面。
6.1.1 文本界面的实现与特点
文本界面(CLI)依靠字符的显示来传递信息,它通常不需要复杂的图形渲染技术,因此在资源受限的环境中表现良好。文本界面的设计通常涉及字符串的布局、格式化以及对输入的处理。
下面的代码展示了一个简单的文本界面数独游戏的初始化实现(使用Python):
import random
def print_board(board):
for row in board:
print(" ".join(str(num) if num != 0 else '.' for num in row))
def is_valid(board, row, col, num):
# 检查行
for x in range(9):
if board[row][x] == num:
return False
# 检查列
for x in range(9):
if board[x][col] == num:
return False
# 检查3x3宫格
start_row, start_col = 3 * (row // 3), 3 * (col // 3)
for i in range(3):
for j in range(3):
if board[i + start_row][j + start_col] == num:
return False
return True
def solve_sudoku(board):
empty = find_empty_location(board)
if not empty:
return True # No more empty space, solution found
row, col = empty
for num in range(1, 10):
if is_valid(board, row, col, num):
board[row][col] = num
if solve_sudoku(board):
return True
board[row][col] = 0 # Reset the current cell for backtracking
return False # Trigger backtracking
# Generate an empty board and solve it
board = [[0 for _ in range(9)] for _ in range(9)]
solve_sudoku(board)
print_board(board)
6.1.2 图形界面的设计与实现
图形用户界面(GUI)提供了更丰富的交互方式和视觉体验。在设计图形界面时,我们需要考虑元素的布局、色彩搭配以及用户的操作流程。对于数独游戏而言,一个直观的网格布局、数字输入和候选项标记功能是必不可少的。
接下来是一个简单的图形界面实现,使用Python的Tkinter库:
import tkinter as tk
class SudokuGame:
def __init__(self, master):
self.master = master
self.board = [[0 for _ in range(9)] for _ in range(9)]
self.create_widgets()
def create_widgets(self):
for i in range(9):
for j in range(9):
entry = tk.Entry(self.master, width=2, justify='center', state='readonly')
entry.grid(row=i, column=j)
if self.board[i][j] != 0:
entry.insert(0, str(self.board[i][j]))
def update_value(self, entry, row, col, value):
entry.delete(0, tk.END)
entry.insert(0, str(value))
self.board[row][col] = value
# Create the application window
root = tk.Tk()
root.title("Sudoku Game")
# Initialize the Sudoku game
game = SudokuGame(root)
game.grid()
# Start the application loop
root.mainloop()
6.2 性能优化与测试
性能优化是确保数独游戏运行流畅的关键步骤。在性能优化中,剪枝技巧和预计算数据结构的设计是常见的方法。
6.2.1 剪枝技巧在性能优化中的应用
剪枝技巧是指在数独求解过程中,通过逻辑判断排除不可能的数值,减少求解路径,提高求解效率。这种方法可以显著减少需要考虑的候选项,从而加快求解速度。
例如,当我们解决一个数独问题时,如果某个数字在一个行、列或3x3宫格内仅有一个可能的位置,那么我们可以立即放置这个数字,而不需要进一步的回溯。
6.2.2 预计算数据结构的设计与效果
预计算可以用来存储那些在游戏运行过程中不会改变的数据,例如每个3x3宫格的行、列索引等。通过预计算这些数据,我们可以避免在运行时重复计算,这在一定程度上可以提升游戏性能。
例如,我们可以创建一个字典,其中每个键对应一个3x3宫格的起始行和列索引:
precomputed = {
'top_left': (0, 0), 'top_middle': (0, 3), 'top_right': (0, 6),
'middle_left': (3, 0), 'middle_middle': (3, 3), 'middle_right': (3, 6),
'bottom_left': (6, 0), 'bottom_middle': (6, 3), 'bottom_right': (6, 6),
}
6.3 源代码与持续集成/部署
源代码管理工具和持续集成/部署(CI/CD)流程是现代软件工程中不可或缺的实践,它们可以帮助团队成员有效地协作并确保软件的高质量交付。
6.3.1 源代码管理工具Git的使用
Git是目前广泛使用的分布式版本控制系统,它支持团队成员在不同分支上独立地开发和合并代码。下面是一些常见的Git命令:
-
git clone <repository>: 克隆远程仓库到本地。 -
git branch <branch>: 创建一个新的分支。 -
git checkout <branch>: 切换到指定的分支。 -
git add <file>: 将文件添加到暂存区。 -
git commit -m "commit message": 提交更改。 -
git push origin <branch>: 推送本地分支到远程仓库。
6.3.2 持续集成与持续部署(CI/CD)流程介绍
持续集成(CI)是指开发人员频繁地(有时甚至每天多次)将代码集成到共享仓库中。每次集成都通过自动化的构建(包括编译、测试等)来验证,从而尽早发现集成错误。
持续部署(CD)是CI的下一步,它自动化了软件的发布过程。一旦代码变更通过了所有测试,它将自动被部署到生产环境。
CI/CD流程通常包括以下几个步骤:
- 开发者向版本控制系统提交代码变更。
- 自动触发构建系统开始构建并执行测试。
- 测试通过后,代码变更被自动部署到预生产环境。
- 通过更多的测试(例如性能测试)后,自动部署到生产环境。
在实践中,可以使用工具如Jenkins、GitLab CI或GitHub Actions等来实现CI/CD的自动化流程。
简介:数独是一款基于逻辑的数字填充游戏,要求在9x9格子中填入数字,满足每行、每列及九个3x3宫格内数字1至9不重复。Sudoku-game项目旨在创建一个完整的数独游戏系统,包括生成器和求解器。生成器负责创建具有唯一解的数独谜题,而求解器则找出给定初始条件下所有可能的解决方案。该项目使用C++编程语言,涉及到多种算法设计、数据结构、用户界面设计、性能优化和测试调试。此外,项目还可能包含源代码管理和持续集成/持续部署(CI/CD)的实践。
























 2248
2248

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








