题目:设椭圆
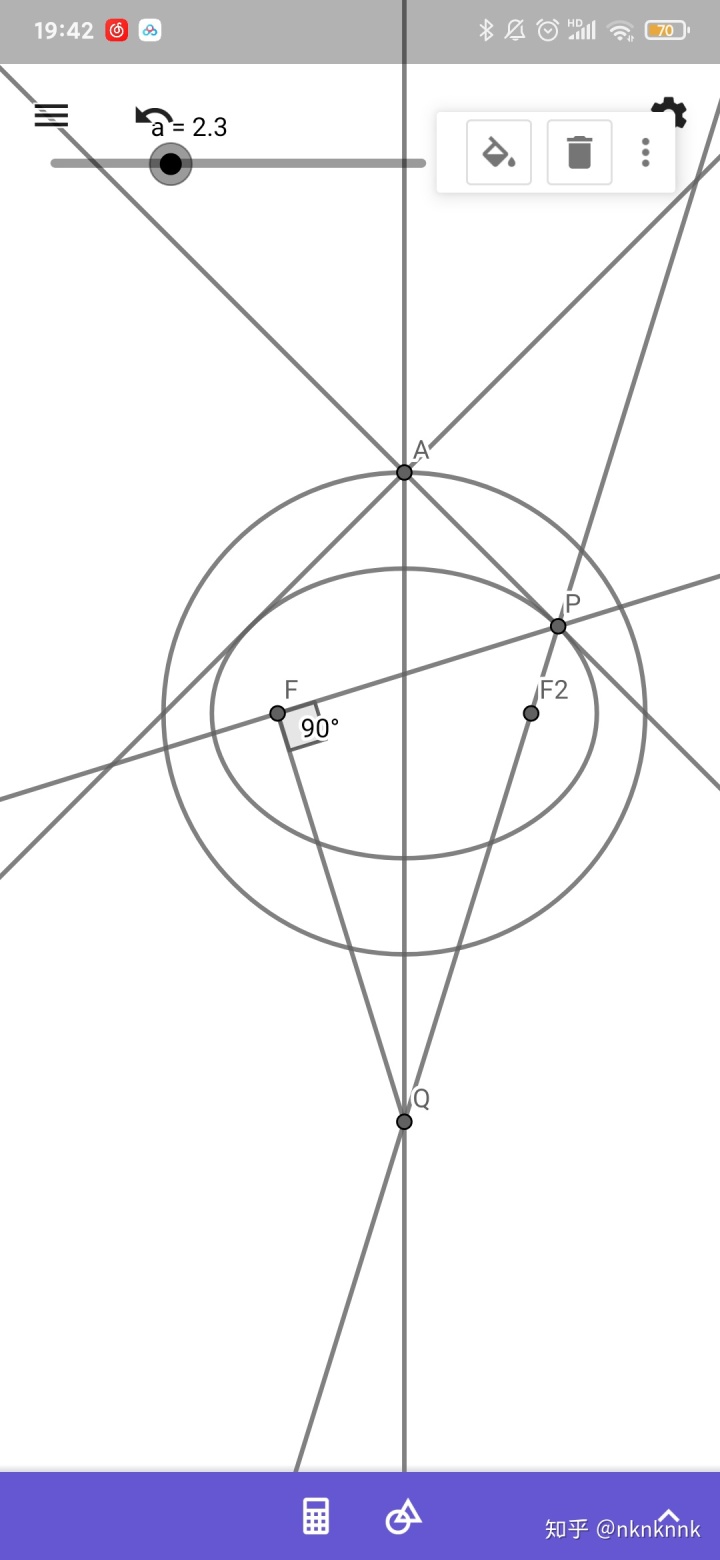
分析:
- 椭圆外准圆半径
, 与所给直线恰好交于
轴同一点。如果作出于所给直线对称的直线
,该直线与椭圆也有交点,而这两条直线在
处的交角恰为直角,由准圆的性质可以知道,
为椭圆的切线。
- 直线
,
关于
轴对称,显然
经过椭圆左侧的切点。
接下来我们利用这两个切点给出证明。
首先添加一点辅助线。
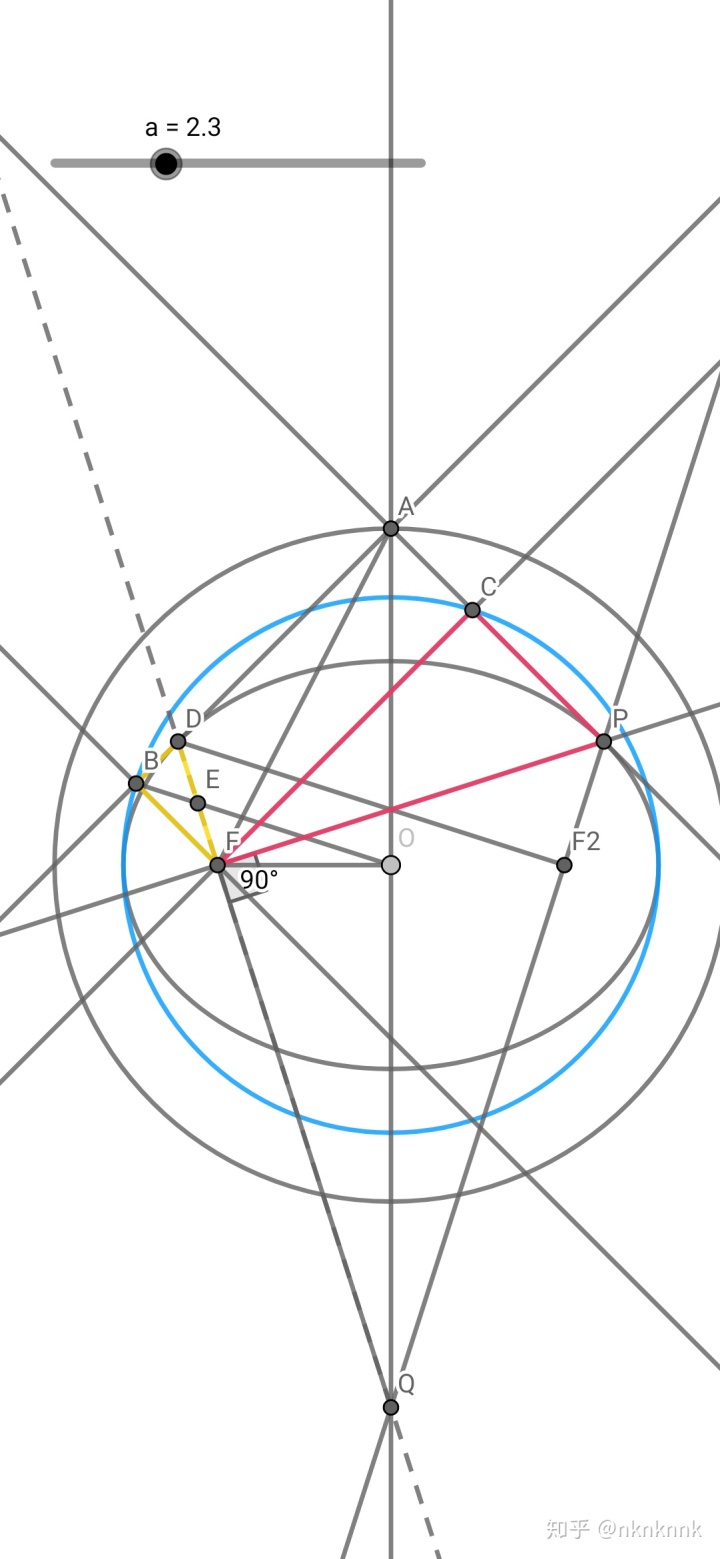
我们的目标是证明
证明:设左切点为
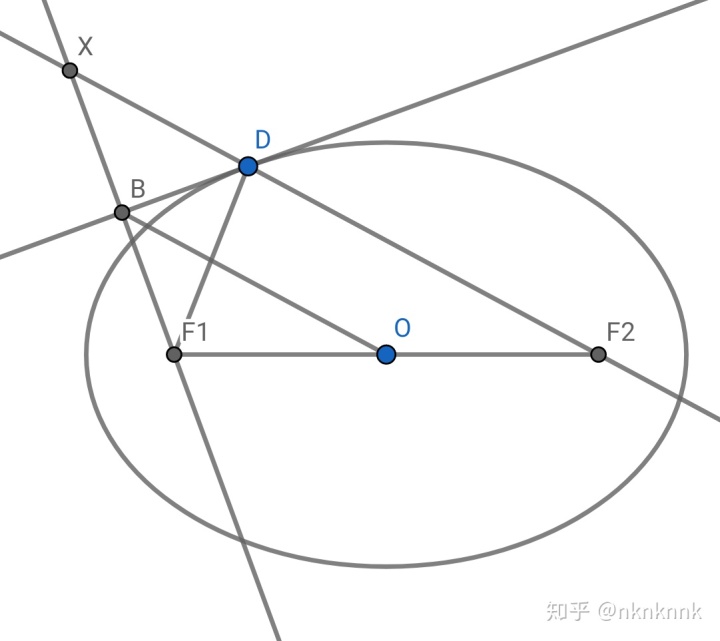
延长
综上所述,
结论:
题目:设椭圆

分析:
接下来我们利用这两个切点给出证明。
首先添加一点辅助线。

我们的目标是证明
证明:设左切点为

延长
综上所述,
结论:

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


