1、函数
 的图象
的图象
(1)简谐运动的有关概念
简谐运动图
象的解析式
振幅
周期
频率
相位
初期

A




(2)五点作图法
①先确定周期
 ,作出在一个周期内的图象.
,作出在一个周期内的图象.
②令
 ,由X分别取0,
,由X分别取0,
 ,
,
 ,
,
 ,
,
 ,求出对应的x值列表如下:
,求出对应的x值列表如下:

0




x






0
A
0
-A
0
③描点画图,再利用函数的周期性,把所得简图向左右分别扩展从而得到
 的简图(但一般这步只作叙述,图象上不体现出来).
的简图(但一般这步只作叙述,图象上不体现出来).
温馨提示
(1)函数
 ,
,
 及
及
 的图象均可用五点法作出.
的图象均可用五点法作出.
(2)当画函数
 在某个指定区间上的因象时,一般先求出
在某个指定区间上的因象时,一般先求出
 的范围,然后在这个范围内选取特征点,连同区间的两个端点一起列表.
的范围,然后在这个范围内选取特征点,连同区间的两个端点一起列表.
知识2由
 的图象得到
的图象得到
 (其中
(其中
 )的图象的过程
)的图象的过程
先画出函数
 的图象,再把正弦曲线向左(右)平移个单位长度,得到
的图象,再把正弦曲线向左(右)平移个单位长度,得到
 的图象,然后使曲线上各点的横坐标变为原来的
的图象,然后使曲线上各点的横坐标变为原来的
 ,得到函数
,得到函数
 的图象,最后把曲线上各点的纵坐标变为原来的A倍,得到函数
的图象,最后把曲线上各点的纵坐标变为原来的A倍,得到函数
 的图象.
的图象.
这一过程的步骤如下:



应注意还有一种途径:



这两个途径的关键差别在“相位变换”这一步骤上,其实质是要看自变量x的变化情况对于第一种途径,在相位变换这一步中是由x变到
 ,故应为“将函数
,故应为“将函数
 图象上所有点向左(当
图象上所有点向左(当
 时)或向右(当
时)或向右(当
 时)平移
时)平移
 个单位长度得到函数
个单位长度得到函数
 的图象”;对于第二种途径,在相位变换这一步中是由
的图象”;对于第二种途径,在相位变换这一步中是由
 变到
变到
 即
即
 ,实质是x变化到
,实质是x变化到
 ,故应为“将函数
,故应为“将函数
 的图象上所有点向左(当
的图象上所有点向左(当
 时或向右(当
时或向右(当
 时)平移
时)平移
 个单位长度得到函数
个单位长度得到函数
 的图象”.两者平移的方向相同,但平移的单位长度不同,这是很容易出错的地方.
的图象”.两者平移的方向相同,但平移的单位长度不同,这是很容易出错的地方.
温馨提示
(1)由
 得到
得到
 的过程体现了由简单到复杂,由特殊到一般的化归思想.
的过程体现了由简单到复杂,由特殊到一般的化归思想.
(2)若
 中的
中的
 ,可先用诱导公式把x前的系数变为正的,再进行变为
,可先用诱导公式把x前的系数变为正的,再进行变为
正的,再进行交换.
3、
 (
(
 )的性质
)的性质
(1)定义域
 的定义域为R
的定义域为R
(2)值域
 的值域为
的值域为

(3)周期性
 的周期
的周期

(4)奇偶性
当
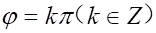 时,函数为奇函数;当
时,函数为奇函数;当
 时函数为偶函数.
时函数为偶函数.
(5)单调性
函数
 (A>0,0>0,
(A>0,0>0,
 )的单调增区间可由
)的单调增区间可由
 解得;单调减区间可由
解得;单调减区间可由
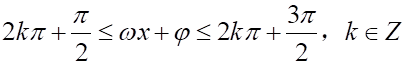 解得.
解得.
(6)对称心
 的对称中心的磺坐标可由
的对称中心的磺坐标可由
 解得,纵坐标为0.
解得,纵坐标为0.
(7)对称轴
 的对称轴方程可由
的对称轴方程可由
 解得.
解得.
知识拓展
(1)
 的对称中心的横坐标可由
的对称中心的横坐标可由
 解得,纵坐标为0.
解得,纵坐标为0.
 的对称轴方程可由
的对称轴方程可由
 解得.
解得.
(2)三角函数图象的几种常见变换
①振幅变换:


②周期变换:

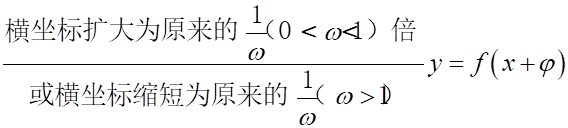
③相位变换:


④平移变换:


⑤对称变换:

 +y=f(
+y=f(
鲸准教学方法
1、由面数图象确定
 的解析式
的解析式
给出一段曲线及某些关键点的坐标,,求函数
 的解析式,其结论不唯一,一般根据图象具体情况选定一个简洁的表达形式即可这类问题主要用“五点法”来确定其中的系数.
的解析式,其结论不唯一,一般根据图象具体情况选定一个简洁的表达形式即可这类问题主要用“五点法”来确定其中的系数.
(1)A:一般可由图象上的最大值、最小值来确定
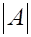
(2)
 因为
因为
 二,所以往往通过求周期T来确定
二,所以往往通过求周期T来确定
 .曲线与x轴的相邻的两个交点之间的距离为
.曲线与x轴的相邻的两个交点之间的距离为
 ;
;
相邻的最高点与最低点横坐标之差的绝对值为
 ;相邻的两个最高点(或最低点)之间的距离为T.
;相邻的两个最高点(或最低点)之间的距离为T.
(3)
 :从寻找“五点法”中的第一零点
:从寻找“五点法”中的第一零点
 (也叫初始点作为突破口,要从图象的升降情况找准第一零点的位置.
(也叫初始点作为突破口,要从图象的升降情况找准第一零点的位置.
温馨提示
A,
 ,
,
 三个量中初相φ的确定是一个难点,除使用初始点
三个量中初相φ的确定是一个难点,除使用初始点
 外,还可利用五点法确定初相
外,还可利用五点法确定初相
 ,即在五点中找两个特殊点列方程组解出
,即在五点中找两个特殊点列方程组解出
 .
.
1如图是函

 的部分图象求此函数的解析式.
的部分图象求此函数的解析式.
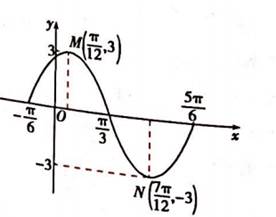
解析由题中的函数图象,得A=3,
 ,
,
 ,
,
所以
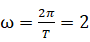 .
.
所以函数
 .
.
将点
 代入
代入
 中,
中,
得
 ,
,
所以
 .
.
所以
 ,
,
所以
 .
.
因为
 ,所以
,所以
 .
.
所以所求函数解析式是
 .
.
温馨提示
确定
 的解析式的步骤:
的解析式的步骤:
(1)求
 .先确定函数的最大值M和最小值m,则
.先确定函数的最大值M和最小值m,则
 ,
,
 .
.
(2)求
 .相邻的最高点与最低点横坐标之差的绝对值为
.相邻的最高点与最低点横坐标之差的绝对值为
 ;相邻的两个最高点(或最低点)之间的距离为T,再根据
;相邻的两个最高点(或最低点)之间的距离为T,再根据
 确定
确定
 .
.
(3)求
 .常用的方法:
.常用的方法:
①代入法:把图象上的一个已知点的坐标代入(此时A,
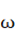 ,b已知).
,b已知).
②五点法:确定
 值时,往往以寻找“五点法”中的一个点为突破口.“第一点”即图象上升时与x轴的交点,此时
值时,往往以寻找“五点法”中的一个点为突破口.“第一点”即图象上升时与x轴的交点,此时
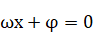 ;“第二点”即图象的“峰点”,此时
;“第二点”即图象的“峰点”,此时
 ;“第三点”即图象下降时与x轴的交点,此时
;“第三点”即图象下降时与x轴的交点,此时
 ;“第四点”即图象的“谷点”,此时
;“第四点”即图象的“谷点”,此时
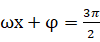 ;“第五点”,此时
;“第五点”,此时
 .另外,要特别注意已知条件中所给的
.另外,要特别注意已知条件中所给的
 的范围.
的范围.
2 利用三角函数图象变换解题
(1)振幅变换:
 .
.
将
 的图象上各点的纵坐标变为原来的A倍(横坐标不变).
的图象上各点的纵坐标变为原来的A倍(横坐标不变).
(2)相位变换:
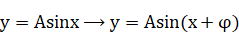 .
.
将
 的图象上所有点向左
的图象上所有点向左
 或向右
或向右
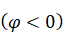 平移
平移
 个单位长度.
个单位长度.
(3)周期变换:
 .
.
将
 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的
 (纵坐标不变).
(纵坐标不变).
(4)由
 的图象变换到
的图象变换到
 的图象.一般先作相位变换,然后作周期变换,最后作振幅变换,即
的图象.一般先作相位变换,然后作周期变换,最后作振幅变换,即
 .如果先作周期变换,后作相位变换,则左(右)平移时不是
.如果先作周期变换,后作相位变换,则左(右)平移时不是
 个单位长度,而是
个单位长度,而是
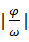 个单位长度,即
个单位长度,即
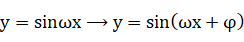 是向左(或向右)平移
是向左(或向右)平移
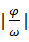 个单位长度.
个单位长度.
例2 已知函数
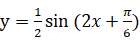 ,该函数的图象如何由
,该函数的图象如何由
 的图象经过变换得到?
的图象经过变换得到?
解析 解法一:①将函数
 的图象向左平移
的图象向左平移
 个单位长度,可以得到函数
个单位长度,可以得到函数
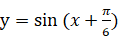 的图象;
的图象;
②把
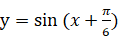 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的
 ,纵坐标不变,可以得到函数
,纵坐标不变,可以得到函数
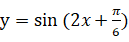 的图象;
的图象;
③将函数
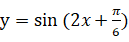 的图象上各点的纵坐标缩短到原来的
的图象上各点的纵坐标缩短到原来的
 ,横坐标不变,可以得到函数
,横坐标不变,可以得到函数
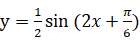 的图象.
的图象.
解法二: ①将函数
 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的
 ,纵坐标不变,得到函数
,纵坐标不变,得到函数
 的图象;
的图象;
②将
 的图象向左平移
的图象向左平移
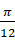 个单位长度,可以得到函数
个单位长度,可以得到函数
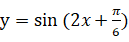 的图象;
的图象;
③将
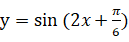 的图象上的各点的纵坐标缩短到原来的
的图象上的各点的纵坐标缩短到原来的
 ,横坐标不变,可以得到函数
,横坐标不变,可以得到函数
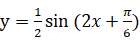 的图象.
的图象.
3 求三角函数的单调区间
求形如
 或
或
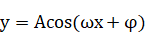 (其中
(其中
 的函数的单调区间,可以通过解不等式去求,列不等式的原则是:①把“
的函数的单调区间,可以通过解不等式去求,列不等式的原则是:①把“
 ”视为一个“整体”;②当
”视为一个“整体”;②当
 (或
(或
 时,所列不等式与
时,所列不等式与
 或
或
 的单调区间对应的不等式相同(相反).
的单调区间对应的不等式相同(相反).
例3 已知函数
 的最小正周期是
的最小正周期是
 .
.
(1)求
 的值;
的值;
(2)若
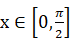 ,且
,且
 ,求
,求
 的值;
的值;
(3)求
 的单调区间.
的单调区间.
解析 (1)因为
 的最小正周期是
的最小正周期是

所以
 ,所以
,所以
 .
.
(2)由(1)得
 .
.
因为
 ,所以
,所以
 .
.
因为
 ,
,
所以
 .
.
所以
 ,
,
解得
 .
.
(3)由
 ,
,
得
 .
.
所以
 的单调递增区间为
的单调递增区间为
 ,
,
 .
.
由
 ,
,
得
 .
.
故
 的单调递减区间为
的单调递减区间为
 ,
,
 .
.
4 函数
 的图象的对称问题
的图象的对称问题
(1)函数
 的图象关于直线
的图象关于直线
 (其中
(其中
 )对称,也就是说,过波峰或波谷处且与
)对称,也就是说,过波峰或波谷处且与
 轴垂直的直线为其对称轴.
轴垂直的直线为其对称轴.
(2)函数
 的图象关于点
的图象关于点
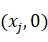 (其中
(其中
 )中心对称,也就是说,函数图象与
)中心对称,也就是说,函数图象与
 轴的交点(平衡位置点)是其对称中心.
轴的交点(平衡位置点)是其对称中心.
例4 已知函数
 在一个周期内的图象如图所示.若方程
在一个周期内的图象如图所示.若方程
 在区间
在区间
 上有两个不同的实数解
上有两个不同的实数解
 ,则
,则
 的值为
的值为

A.
 B.
B.
 C.
C.
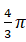 D.
D.
 或
或

解析 要使方程
 在区间
在区间
 上有两个不同的实数解,只需函数
上有两个不同的实数解,只需函数
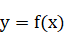 与函数
与函数
 的图象在区间
的图象在区间
 上有两个不同的交点,由题图知,两个交点关于直线
上有两个不同的交点,由题图知,两个交点关于直线
 或
或
 对称,因此
对称,因此
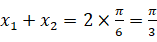 或
或
 .
.
答案 D
5 求三角函数的周期
(1)可利用公式求三角函数周期.
(2)画出三角函数的图象求周期.
例5 求下列函数的最小正周期.
(1)
 ;
;
(2)
 .
.
解析 (1)
 .
.
(2)画出函数
 的图象,如图,由图象可知
的图象,如图,由图象可知
 .
.

6 “五点法”作三角函数图象
作三角函数的图象,关键是找出与x相对应的五个点,一般令
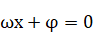 ,
,
 ,
,
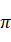 ,
,
 ,
,
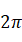 ,即可得到绘图所需的五个点的坐标,其中x的取值依次成等差数列,公差为
,即可得到绘图所需的五个点的坐标,其中x的取值依次成等差数列,公差为
 ,同时,若要求画出给定区间上的函数图象,应适当调整
,同时,若要求画出给定区间上的函数图象,应适当调整
 的取值,以便列表时能使x在给定的区间内取值.
的取值,以便列表时能使x在给定的区间内取值.
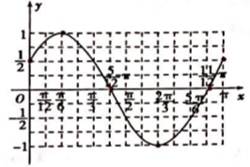
例6 设函数
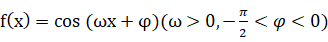 最小正周期为
最小正周期为
 ,且
,且
 .
.
(1)求
 和
和
 的值;
的值;
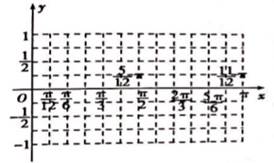
(2)在给定坐标系中作出函数
 在
在
 上的图象.
上的图象.
解析 (1)由题意知
 ,
,
所以
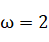 ,所以
,所以
 ,
,
又
 ,
,
所以
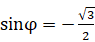 ,
,
所以
 ,
,
又
 ,所以
,所以
 .
.
(2)由(1)得
 ,列表如下:
,列表如下:


0

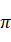


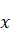
0




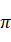


1
0

0

画出图象如图.







 本文详细介绍了函数y=Asin(wx+φ)的图象特点,包括振幅、周期、频率、相位、初期等概念,并阐述了五点作图法来绘制函数图象。此外,讨论了函数的对称中心、单调性和周期性等性质,并提供了由y=sinx到y=Asin(wx+φ)的图象变换过程。文章还探讨了如何利用三角函数图象解决相关问题,如求解析式、单调区间、对称性等,并给出了例题解析。
本文详细介绍了函数y=Asin(wx+φ)的图象特点,包括振幅、周期、频率、相位、初期等概念,并阐述了五点作图法来绘制函数图象。此外,讨论了函数的对称中心、单调性和周期性等性质,并提供了由y=sinx到y=Asin(wx+φ)的图象变换过程。文章还探讨了如何利用三角函数图象解决相关问题,如求解析式、单调区间、对称性等,并给出了例题解析。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








