内容结构指引
计算流体力学概述 | 流体力学的一些基本概念 | 流体力学的控制方程
粘性流动的控制方程（纳维-斯托克斯方程） | 无粘流的控制方程（欧拉方程）
适合CFD的控制方程 | NS方程的无量纲化 | 简化NS方程
主要名词检索
计算流体力学（CFD） | 离散化 | 连续介质假设 | 流动微团 | 控制体 | 流动模型 | 物质导数
当地导数 | 迁移导数 | 速度散度 | 拉格朗日描述 | 欧拉描述 | 控制方程 | 连续性方程 | 动量方程
能量方程 | 守恒型 | 非守恒型 | 纳维-斯托克斯方程 | 欧拉方程 | 守恒型方程的向量形式
通向量 | 源项 | 解向量 | 无量纲量 | 特征量 | 无量纲化 | 定常流方程 | 不可压流方程
边界层方程 | 小扰动方程
计算流体力学概述
a. 定义
计算流体力学（CFD）是 通过数值方法求解流体力学控制方程，得到流场的离散定量描述，并以此预测流体运动规律的学科。
实际问题的流动控制方程复杂，解析解难以获得，我们通常采用数值方法求解，值得一提的是，在计算机产生之前，数值方法已然产生。
离散化分为流场的离散化（网格生成）与方程的离散化（计算格式）
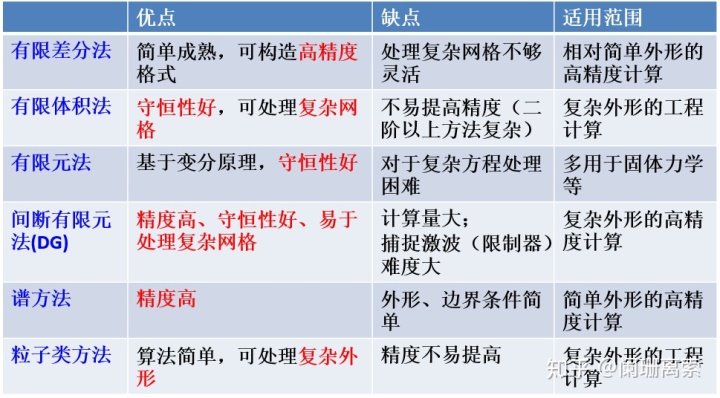
b. CFD常用方法
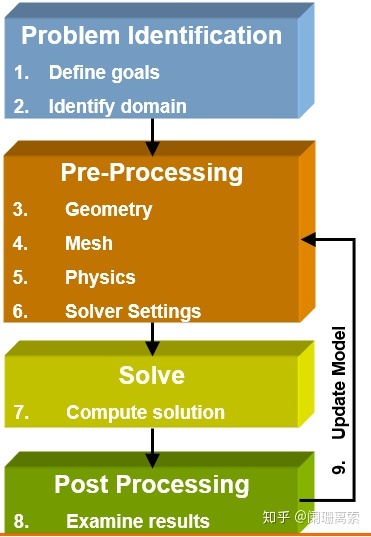
c. CFD流程
问题定义（确定模拟目的、确定计算域）
前处理和求解（创建几何实体、设计划分网格、设置物理问题、定义求解器、求解监控）
后处理过程（查看计算结果、修订模型）
流体力学的一些基本概念
1）连续介质假设：流体连续地充满整个空间
2&#x
最低0.47元/天 解锁文章
2150
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
