QC十四大手法全面指南：高效解决问题与质量提升

本文还有配套的精品资源，点击获取

简介：QC（Quality Control）十四大手法是全面质量管理中的核心工具集，源自日本的TQM，广泛应用于全球范围内的问题识别、分析和解决。本指南详细介绍了这十四种手法，包括检查表、层别法、因果图、直方图、控制图、散点图、柏拉图、运行图、关联图、系统图、矩阵图、箭条图、PDPC法和5W2H法，并说明了它们在实际工作中的应用。掌握这些手法对于持续改进质量、提高工作效率和客户满意度具有重大意义。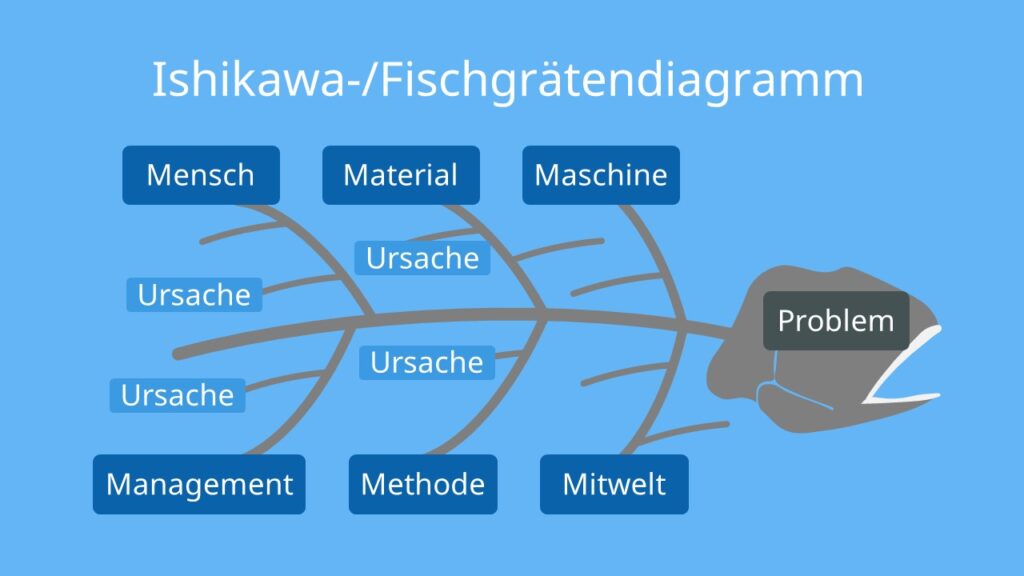

1. QC十四大手法概述与问题解决框架

在质量管理的历史长河中，QC（质量控制）十四大手法始终是关键工具，帮助企业和团队系统地识别、分析和解决质量问题。本章将概述QC手法的框架和解决问题的整体流程，让读者对接下来的深入讨论有一个宏观的认识。

1.1 QC十四大手法简介

QC十四大手法包括了管理图、流程图、检查表、帕累托图、因果图（鱼骨图）、直方图、散点图、控制图、趋势图、关联图、矩阵图、系统图、优先矩阵以及新七种工具。这些工具根据问题的性质和阶段被灵活运用在质量改进的不同环节。

1.2 问题解决的基本框架

问题解决的框架通常遵循PDCA（计划-执行-检查-行动）循环。先对问题进行定义和分解，然后通过数据收集和分析确定问题的根源，制定相应的对策并执行，最终验证效果并进行标准化。

flowchart LR
    A[定义问题] --> B[数据收集与分析]
    B --> C[制定对策]
    C --> D[执行对策]
    D --> E[效果检查]
    E --> F[标准化与巩固成果]
    F --> A

1.3 质量问题解决流程的实践意义

掌握QC十四大手法和问题解决框架对于企业提升产品质量、优化工作流程、提高效率和降低成本至关重要。通过实践这些方法，可以逐步提升企业的整体竞争力和市场适应力。

2. QC数据收集与整理技巧

2.1 检查表的使用和数据收集

2.1.1 检查表的设计原则与应用

检查表是一种常用的质量控制工具，它通过结构化的表格形式，记录特定数据，以便于分析和改进。设计一个好的检查表应遵循以下几个原则：

1. 目标明确 ：检查表的设计应始终围绕质量控制的目标，确保收集的数据能够反映问题的关键方面。
2. 简单直观 ：表格结构应尽量简单，确保记录者可以快速且准确地填写信息。
3. 易于分析 ：数据应以易于分析的格式呈现，例如分类或分段计数，以便于后期统计和图形化展示。
4. 持续更新 ：检查表应具有一定的灵活性，便于根据实际情况进行调整和优化。

在应用检查表时，应确保所有相关人员对表单的填写规范有明确共识，并且能够在数据收集过程中保持一致性。

2.1.2 数据收集的方法与技巧

数据收集是质量控制过程中的关键步骤，以下是一些数据收集的有效方法和技巧：

1. 标准化流程 ：建立标准化的数据收集流程，确保数据的准确性和可靠性。
2. 培训记录者 ：对记录数据的人员进行适当的培训，以确保他们了解收集数据的重要性和正确的方法。
3. 定期更新 ：定期回顾和更新检查表，确保其仍然符合当前的质量控制目标。
4. 自动化工具 ：使用电子表格软件或专业的数据收集工具来自动化数据录入和初步分析过程，提高效率和减少人为错误。

2.2 层别法（帕累托图）识别主要问题

2.2.1 帕累托图的基本原理

帕累托图是基于帕累托原则（80/20法则），即80%的问题往往由20%的原因造成。帕累托图通过柱状图和折线图结合的方式，帮助识别出造成质量问题的关键少数因素。

在制作帕累托图时，通常包括以下步骤：

1. 数据分类 ：将数据按照不同的类别进行分类。
2. 数据汇总 ：计算每个类别的总和。
3. 绘制柱状图 ：根据数据总和绘制柱状图，柱状按大小从高到低排列。
4. 绘制累积曲线 ：在柱状图上绘制累积百分比曲线，标识出累积百分比达到80%的关键少数类别。

2.2.2 利用帕累托图识别关键问题

一旦帕累托图绘制完成，关键问题的识别过程如下：

1. 确定主要因素 ：识别出哪些因素的累积百分比首先达到或超过80%。
2. 优先级排序 ：将识别出的主要因素按照其对总问题的影响程度进行排序。
3. 问题解决 ：优先解决那些影响最大的问题因素，以期达到最佳的质量改进效果。

通过层别法，企业可以集中资源和注意力来解决那些真正影响产品和服务质量的关键问题。以下是帕累托图的一个实例：

%%{init: {'theme': 'default'}}%%
pie title 帕累托图案例
  "类别A" : 50
  "类别B" : 20
  "类别C" : 15
  "其他类别" : 15

通过以上步骤和逻辑分析，我们可以有效地运用层别法和帕累托图来识别和解决主要问题。这不仅可以提升质量管理的效率，还能显著提升产品质量和客户满意度。

3. QC分析方法与统计技术

3.1 因果图（鱼骨图）分析问题根源

3.1.1 鱼骨图的构成与绘制步骤

鱼骨图，又称因果图，是QC七大工具之一，用于系统地表示一个问题的原因与其结果之间的关系。它通过图形化的方式，帮助我们识别、分类并可视化潜在的原因。

一个完整的鱼骨图包括以下主要构成部分：

• 问题陈述（鱼头） ：位于图的最右侧，清晰地定义问题。
• 主要因素类别（大鱼骨） ：从问题陈述向外延伸，通常包括了操作、人员、机器、材料、方法、测量和环境等几个大的类别。
• 次级因素（小鱼骨） ：连接到大鱼骨上，是潜在原因的具体表现。
• 原因（鱼刺） ：位于小鱼骨上，是导致问题的最细小的因素。

绘制鱼骨图的基本步骤如下：

1. 定义问题 ：清晰而具体地描述问题或缺陷，将其置于图的右侧。
2. 确定主要因素类别 ：这些类别作为主鱼骨，如上所述，从问题陈述向左延伸。
3. 识别次级因素 ：对每个主要因素，考虑可能的次级因素，并将其作为小鱼骨与主要因素连接。
4. 挖掘根本原因 ：进一步细化每个次级因素，找出更具体的原因，并将它们作为鱼刺添加到图中。
5. 评审和验证 ：通过团队讨论，验证每条鱼刺是否合理，是否对问题有直接影响。
6. 确定和采取行动 ：基于分析结果，确定可能的解决方案并采取行动。

以下是绘制鱼骨图的一个简单代码块示例：

graph TD
    A[问题陈述] --> B[操作]
    A --> C[人员]
    A --> D[机器]
    A --> E[材料]
    A --> F[方法]
    A --> G[测量]
    A --> H[环境]

这个代码块使用了Mermaid语法，它是一个基于文本的图表工具，可以用来绘制流程图、状态图、甘特图等，非常适合用来描述鱼骨图的构成。

3.1.2 案例分析：利用鱼骨图追溯问题源头

假设我们要分析产品返修率高的问题，可以通过以下步骤使用鱼骨图来追溯问题的源头：

1. 定义问题 ：产品返修率高。
2. 确定主要因素 ：这可能包括操作、人员、机器、材料、方法、测量、环境。
3. 识别次级因素 ：比如在“操作”类别下，可能会有操作失误、操作不熟练等问题。
4. 挖掘根本原因 ：更进一步，我们可能会找到“缺乏培训”、“工作压力大”等导致操作失误的根本原因。
5. 评审和验证 ：团队成员一起检查这些原因是否合理并讨论是否有遗漏。
6. 确定和采取行动 ：基于分析结果，可能的解决方案包括制定详细的操作培训计划、改善工作环境等。

通过这样的分析，团队不仅能识别问题的根源，还能激发潜在的解决方案。值得注意的是，鱼骨图并不用于证明因果关系，而是用于探索可能的因果关系，并激发讨论和深入思考。

3.2 直方图统计分布展示和数据分析

3.2.1 直方图的绘制与解读

直方图是QC中用于展示数据分布的图形工具，它能帮助我们直观地理解数据的集中趋势、分散程度和分布形状。通过直方图，我们能够对数据集有一个快速的视觉评估。

绘制直方图的步骤如下：

1. 收集数据 ：首先需要收集一定数量的数据点。
2. 确定组距和组数 ：根据数据的范围和想要观察的细节程度，决定每个柱子代表的区间大小和总共有多少个柱子。
3. 统计频数 ：计算每个区间（组距）内的数据点个数。
4. 绘制柱状图 ：以每个区间的左边界为基线，绘制高度对应频数的柱子。
5. 分析直方图 ：观察柱状图的形状、集中趋势、异常值等特征。

一个简单的直方图的代码块示例：

import matplotlib.pyplot as plt

data = [1, 2, 3, 3, 4, 4, 5, 5, 5, 6, 7, 8, 9, 10]  # 示例数据
plt.hist(data, bins=5)  # 绘制直方图，分成5个区间
plt.title('直方图示例')
plt.xlabel('区间')
plt.ylabel('频数')
plt.show()

这段代码使用了Python的matplotlib库来绘制直方图。代码逻辑中，“bins=5”定义了组数，而 plt.hist(data, bins=5) 负责生成柱状图。

3.2.2 数据分布的统计分析应用

直方图不仅帮助我们以图形化的方式观察数据，还可以对数据集进行初步的统计分析。例如，通过观察直方图的形状，我们可以初步判断数据分布的类型（如正态分布、偏态分布等）。此外，直方图的集中趋势（通过数据分布的中心位置判断）和分散程度（柱子宽度和高度的变化）都是对数据集的重要描述。

在质量控制中，直方图是监控生产过程稳定性的工具。如果在生产过程中，绘制的直方图显示数据分布发生偏移或形状发生改变，可能表明生产过程出现了问题，需要进行调整。

例如，在一个稳定的过程中，如果直方图突然出现了不正常的偏斜或峰度变化，可能意味着机器出现了磨损，材料的成分发生了变化，或者是操作人员的操作方法出现了问题。通过进一步的调查和分析，我们能够定位问题并采取相应的措施进行纠正。

总之，直方图是QC分析方法中一个非常有用的工具，能够帮助我们快速识别和解决问题。直方图的应用不仅限于生产过程中的质量控制，还可以广泛应用于项目管理、产品开发和其他需要数据分析的领域。

4. QC监控工具与改进策略

4.1 控制图监测过程稳定性

4.1.1 控制图的理论基础

控制图是一种统计学工具，它用于监控和控制生产过程的稳定性和可控性。控制图的基础概念起源于20世纪20年代，由美国工程师沃尔特·休哈特（Walter A. Shewhart）提出，因此也被称为休哈特控制图。控制图的原理基于正态分布理论，利用数据点在上下控制限（Upper Control Limit, UCL和Lower Control Limit, LCL）内的分布状态来判断过程是否处于统计控制状态。

在控制图中，中心线（Central Line, CL）代表过程的平均值，而上下控制限是根据过程变异性（通常是标准差）计算得出的。当数据点落在控制限内，并且不表现出任何非随机模式时，我们可以认为该过程是稳定的。反之，如果数据点超出控制限，或显示出有规律的模式，那么过程可能受到特殊原因的影响，即过程不处于统计控制状态。

4.1.2 应用控制图进行过程控制

为了使用控制图进行过程控制，首先需要收集过程数据，然后进行以下步骤：

1. 计算过程平均值（CL）和标准差。
2. 确定控制限（UCL和LCL）：标准差的倍数（通常是3倍标准差）。
3. 绘制控制图，并将数据点标在控制图上。
4. 分析控制图，判断过程是否稳定。

在实际操作中，控制图的种类很多，比如X-bar & R图、X-bar & S图、个人控制图（I-MR图）、P图、U图等，每种控制图针对的数据类型和使用场合有所不同。

下面是一个使用Python的简单示例，展示如何绘制一个个人控制图：

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 假设有一组质量检测数据
data = np.array([102, 101, 100, 99, 100, 101, 102, 103, 104, 105])

# 计算平均值和标准差
mean = np.mean(data)
std_dev = np.std(data)

# 确定控制限，一般为3个标准差
UCL = mean + 3 * std_dev
LCL = mean - 3 * std_dev

# 绘制控制图
plt.figure(figsize=(10, 5))

# 绘制中心线、控制限和数据点
plt.axhline(mean, color='r', linestyle='--')
plt.axhline(UCL, color='g', linestyle='--')
plt.axhline(LCL, color='b', linestyle='--')
plt.plot(data, marker='o', linestyle='-', color='m')

plt.title('Individuals and Moving Range (I-MR) Control Chart')
plt.xlabel('Sample')
plt.ylabel('Measurement')
plt.show()

在上述代码中，我们首先导入了所需的库，然后计算了数据的平均值和标准差，接着定义了控制限。最后，我们使用matplotlib绘制了一个简单的控制图，并在图上展示了数据点和控制限。

控制图的解读不仅涉及是否超出了控制限，还要注意数据点是否显示出某些模式，例如周期性波动、趋势、或数据点群聚等，这些都是过程可能不稳定的信号。

4.2 PDPC法预测过程变化和改进计划

4.2.1 PDPC法的工作原理

PDPC（Process Decision Program Chart）法，即过程决策程序图，是一种用于预测和处理项目执行过程中可能出现的问题并制定应对策略的方法。PDPC法通过建立一个树状图来描述项目过程，从目标开始，逐级细化为子目标、任务，直至操作步骤，并识别可能影响项目成功的风险和问题，以及对应的预防措施和应对策略。

PDPC法的核心思想是在项目规划阶段就识别出可能导致项目偏离目标的风险因素，并提前设计出相应的缓解措施，以降低这些风险因素的实际影响。通过PDPC图，项目管理团队可以更系统地识别潜在问题和风险，制定出更全面和有效的风险管理计划。

4.2.2 结合PDPC法制定问题解决策略

结合PDPC法制定问题解决策略的过程通常包括以下几个步骤：

1. 确定目标：明确项目的主要目标和预期成果。
2. 分解过程：将整个项目过程分解为多个子目标和任务。
3. 识别潜在问题：系统地分析在实现每个目标和任务过程中可能遇到的问题和风险。
4. 制定预防和应对措施：针对识别出的问题，制定相应的预防措施和应对策略。
5. 制作PDPC图：将上述信息整合成一个树状图，清晰地展示项目过程和潜在问题及其对应措施。

PDPC图不仅有助于项目管理团队进行问题识别和风险评估，而且也有利于项目成员之间的沟通和信息共享，提高整个团队对项目风险的认识和准备。

通过实施PDPC法，项目团队可以更加有序地处理项目过程中遇到的困难和挑战，提高项目成功的可能性。此外，PDPC图也可以作为项目回顾和复盘的工具，帮助团队总结经验教训，为未来类似项目提供参考。

5. QC图表工具与关联性分析

5.1 散点图判断变量相关性

5.1.1 散点图的基本概念

散点图是一种用于观察两个定量变量之间相关关系的图形工具。通过绘制数据点在两坐标轴上的分布，它可以帮助我们直观地识别变量间是否存在某种线性或非线性关系，甚至可以揭示潜在的模式和趋势。

在质量控制的上下文中，散点图常用于识别产品特性之间的关联，如产品尺寸与重量的关系，或是某种环境因素与产品质量的关系。散点图的X轴和Y轴分别代表两个变量，每个点的位置对应一组变量值的观测结果。

5.1.2 识别和分析变量间的相关性

在使用散点图进行相关性分析时，首先要观察点的分布模式。通常，点的分布沿着一条直线或曲线排列，可以暗示变量之间存在正相关或负相关关系。如果点沿左上至右下的方向排列，表示变量之间存在正相关，即一个变量增加时，另一个变量也倾向于增加；反之，如果点沿右上至左下的方向排列，表示变量之间存在负相关。

在分析时，我们还需要考虑数据点的密度，因为它们可以帮助我们了解关系的强度。紧密聚集的数据点表明关系较为显著；而数据点分布广泛，则可能表示关系较为微弱，或者没有明显的相关性。

为了更精确地衡量变量间的关系，可以计算相关系数（如皮尔逊相关系数）。相关系数的绝对值范围从0到1，值接近1表示变量间有很强的线性关系，接近0则表示没有或很弱的关系。

代码示例：绘制散点图

以下是一个使用Python的matplotlib库来绘制散点图的示例代码：

import matplotlib.pyplot as plt
import numpy as np

# 生成一些模拟数据
x = np.random.rand(50) * 10
y = 2 * x + np.random.randn(50) * 1

# 绘制散点图
plt.scatter(x, y)
plt.title('Scatter Plot Example')
plt.xlabel('Variable X')
plt.ylabel('Variable Y')
plt.show()

执行上述代码后，将生成一个散点图，其中X轴代表变量X，Y轴代表变量Y，图中的散点反映了这两者之间的关系。

5.2 柏拉图比较各类问题影响比例

5.2.1 柏拉图的绘制与分析步骤

柏拉图，又称帕累托图，是一种用于识别问题主要来源的工具，它基于帕累托原则，即少数几个原因往往会造成大部分的问题。柏拉图通过将问题按照频率或影响程度排序，帮助我们集中精力解决最重要的问题。

绘制柏拉图的步骤如下：

1. 数据收集 ：首先收集关于问题类型或原因的数据。
2. 分类汇总 ：根据问题类型或原因进行分类汇总，并计算每个类别问题的出现频率。
3. 计算累计频率 ：计算每个类别问题的累计频率，并根据频率从高到低进行排序。
4. 绘制柱状图和折线图 ：柱状图显示每个问题类别的频率，折线图显示累计频率。
5. 分析与决策 ：依据累计频率划分问题的重要程度，通常累计频率在80%以上的类别被视为主要问题。

5.2.2 优先级排序与资源分配

使用柏拉图可以帮助我们确定资源应该投向哪些问题以达到最大的效益。通常，解决频率最高的问题会带来最显著的改进。

在优先级排序后，我们需要决定资源的分配。资源分配应该考虑以下因素：

• 问题的影响程度 ：问题对整体目标的影响越大，优先级越高。
• 解决的难易程度 ：容易解决的问题可以快速改善，但可能不会带来长远的效益。
• 资源的可用性 ：资源有限，需要合理分配到各个问题上。

有效的资源分配不仅能解决当前问题，还能预防未来问题的发生，从而实现持续改进。

表格示例：柏拉图数据表格

下面是一个柏拉图数据的示例表格，用于展示问题类别、频率、累计频率和优先级：

| 问题类别 | 频率 | 累计频率 | 优先级 | |----------|------|----------|--------| | A | 30 | 30 | 高 | | B | 25 | 55 | 高 | | C | 20 | 75 | 中 | | D | 15 | 90 | 中 | | E | 10 | 100 | 低 |

通过该表格，可以清晰地看到问题A和B的累计频率最高，因此应优先考虑解决。

通过本章节的介绍，我们了解了散点图和柏拉图在分析数据和识别问题中的重要性。通过散点图，我们能够识别变量间的相关性，而柏拉图帮助我们进行问题的优先级排序和资源分配决策。这两种图表工具在质量控制领域中，对于有效识别问题根源和改进方向起到了至关重要的作用。

6. QC综合应用与问题解决策略

6.1 5W2H法问题解决和计划制定

5W2H法是一种非常实用的问题解决和计划制定工具，它将问题和计划分解为七个要素：what（什么）、why（为什么）、who（谁）、where（哪里）、when（何时）、how（如何）和how much（多少）。通过详细阐述这些问题，可以更有条理地进行问题分析和计划制定。

6.1.1 5W2H法的框架与应用

What（什么） 指的是需要解决的问题或要达到的目标是什么。

Why（为什么） 涉及到问题的原因或目标背后的目的。

Who（谁） 是指谁是问题的负责人，或者负责实施计划的人。

Where（哪里） 是问题发生的具体位置或计划执行的地点。

When（何时） 涉及何时开始行动，以及过程或计划的时间表。

How（如何） 是解决问题或执行计划的具体步骤。

How much（多少） 涉及到完成任务所需的资源投入，包括时间、资金、人力等。

6.1.2 基于5W2H法的案例研究

以一家生产工厂提升产品质量为例，5W2H法的应用如下：

• What（什么） ：提升产品的质量合格率。
• Why（为什么） ：提高市场竞争力，减少客户投诉。
• Who（谁） ：质量管理团队。
• Where（哪里） ：在生产线上进行质量检测。
• When（何时） ：立即开始，目标是在三个月内提升合格率达到95%。
• How（如何） ：制定详细的质量改进计划，包括员工培训、设备升级、质量检测标准等。
• How much（多少） ：预算投入，包括培训费用、设备更新费用等。

6.2 综合运用QC工具解决复杂问题

在面对复杂问题时，单独使用一个QC工具往往难以达到理想的效果。因此，综合运用多种QC工具，并掌握它们的联合使用原则与技巧是至关重要的。

6.2.1 多工具联合使用的原则与技巧

• 确定核心问题 ：首先明确要解决的核心问题是什么。
• 选择合适的工具 ：根据问题的性质选择合适的工具进行初步分析。
• 数据收集与分析 ：使用检查表、帕累托图等工具收集数据并进行初步分析。
• 深入挖掘原因 ：通过因果图、直方图等工具深入分析问题的原因。
• 过程控制与改进 ：利用控制图等工具监控过程稳定性，并提出改进措施。
• 计划制定与实施 ：基于5W2H法制定详细的改进计划，并执行。

6.2.2 实际问题解决案例演示

考虑一个实际案例，假设某生产线出现产品合格率下降的问题，我们可以通过以下步骤解决：

1. 确定核心问题 ：产品合格率下降。
2. 数据收集 ：使用检查表收集合格和不合格的产品数据。
3. 初步分析 ：使用帕累托图识别主要不合格因素。
4. 深入挖掘原因 ：利用因果图（鱼骨图）分析导致产品不合格的根本原因。
5. 过程控制 ：通过控制图监控改进措施实施后的过程稳定性。
6. 计划制定与实施 ：依据5W2H法，制定并执行质量改进计划。

通过这种综合应用QC工具的方法，我们可以系统地解决问题，从而提升产品的整体质量。

本文还有配套的精品资源，点击获取

简介：QC（Quality Control）十四大手法是全面质量管理中的核心工具集，源自日本的TQM，广泛应用于全球范围内的问题识别、分析和解决。本指南详细介绍了这十四种手法，包括检查表、层别法、因果图、直方图、控制图、散点图、柏拉图、运行图、关联图、系统图、矩阵图、箭条图、PDPC法和5W2H法，并说明了它们在实际工作中的应用。掌握这些手法对于持续改进质量、提高工作效率和客户满意度具有重大意义。

本文还有配套的精品资源，点击获取